序列的运算

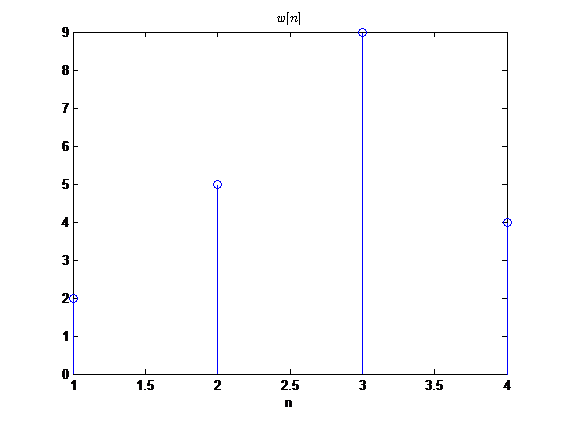
基本运算

调制

  两个序列样本值的乘积，指的是将两个序列的样本值逐点对应相乘，从而得到新的序列：
$y[n]=x[n]w[n]$
在一些应用中，序列的乘积也叫做调制，实现该运算的器件称为调制器。

相乘

  一个序列的每个样本值都乘以标量A以产生新的序列
$y[n]=Ax[n]$
实现相乘运算的器件称为乘法器。

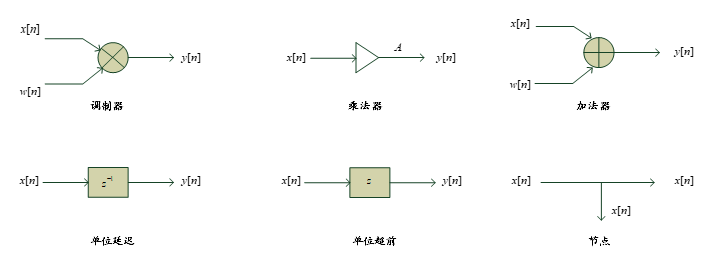
相加

  把两个序列的样本值逐点的相加得到新的序列
$y[n]=x[n]+w[n]$
实现该运算的器件称为加法器。

时移

  时移运算表现为
$y[n]=x[n-N]$
若 $N>0$，则称之为延迟运算，若 $N<0$则称之为超前运算。

  单位延迟为延迟一个单位，即
$y[n]=x[n-1]$
在 $Z$变换中，延迟一个单位相当于乘以 $z^{-1}$，所以在方框图用 $z^{-1}$表示延迟一个单位

  同理，单位超前一个单位可以写为
$y[n]=x[n+1]$
在 $Z$变换中，超前一个单位相当于乘以 $z$，所以在方框图用 $z$表示超前一个单位

反褶

  序列的反褶表现为
$y[n]=x[-n]$

  下面给出一些序列运算的例子，我将以图形的形式给出

调制

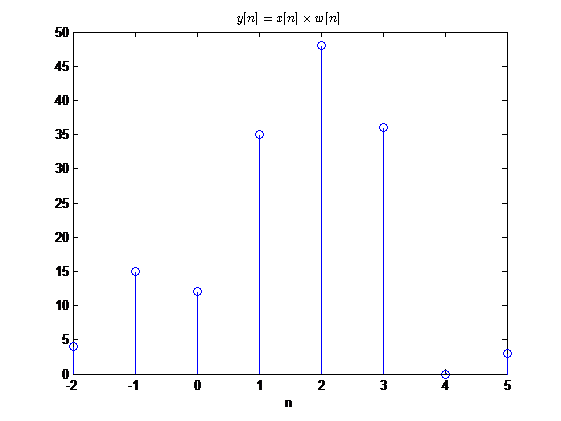
相加

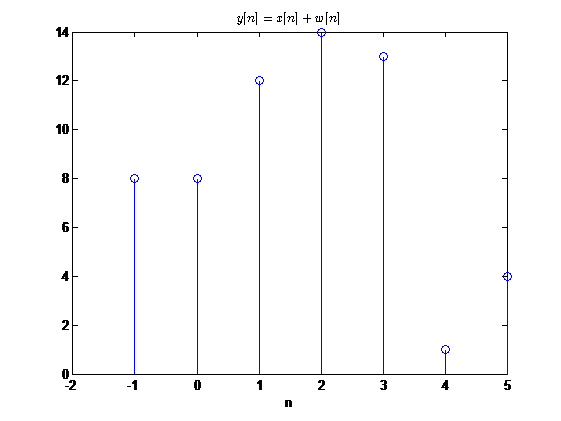
单位延迟

单位超前

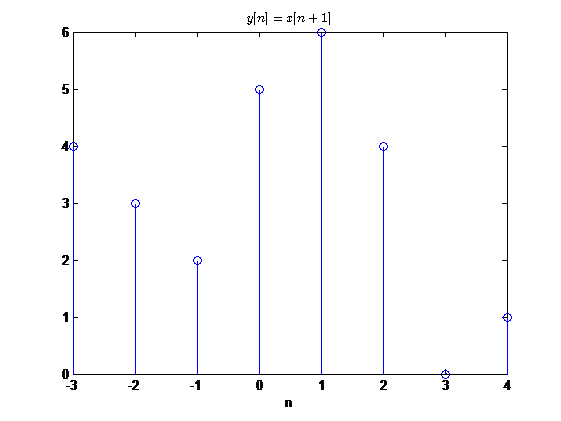
反褶

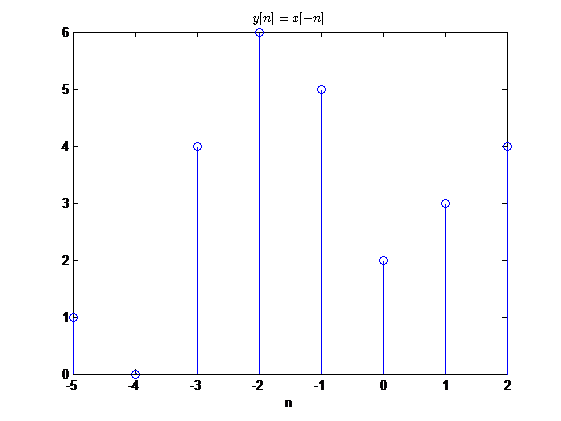
  大多数的应用都是采用上述基本运算的组合。

卷积和

   $x[n]$和 $h[n]$为两个序列，这两个序列通过卷积和后产生新的序列是
$y[n]=\sum_{m=-\infty}^{\infty}x[m]h[n-m]$
至于为什么会有卷积和这种运算，之后在介绍，卷积和可以说是信号与系统分析中最重要的运算之一。

  观察卷积和的表达式，发现卷积和也是由基本运算组成的：首先对 $h[m]$进行反褶得到 $h[-m]$，然后进行时移运算，由 $h[-m]$得到 $h[-(m-n)]=h[n-m]$，然后进行调制运算 $x[m]h[n-m]$，最后进行相加运算得到 $y[n]=\sum_{m=-\infty}^{\infty}x[m]h[n-m]$，所以一个卷积和运算是由反褶，时移，调制，相加等基本运算组成的。

  其实在实际的计算，计算过程就是由我上面所说的过程组成，从这里就可以看到，其实做卷积和运算是比较麻烦的，在学习变换域时，有更好的办法进行卷积和运算。

  卷积和一般也写成 $y[n]=x[n]*y[n]=\sum_{m=-\infty}^{\infty}x[m]h[n-m]$
我们对上面的式子做一个变换，令 $m=n-k$，则：
$y[n]=\sum_{k=-\infty}^{\infty}h[k]x[n-k]=h[n]*x[n]$
所以卷积满足交换律。

不做卷积得到某一项的值

  如何快速展开得到卷积某一项的值，比如想得到 $y[2]$的值。

  假设 $x[n],w[n]$的起点都是 $0$，那么可以快速写出 $y[2]=x[0]w[2]+x[1]w[1]+x[2]w[0]$
观察表达式可以得到 $x$的下标和 $w$的下标加起来等于 $2$，所以想快速得到卷积后某一项的值可以快速的写出来，只要 $x$的下标加上 $w$的下标等于 $n$。

  那么 $y[3]$可以写为

$y[3]=x[0]w[3]+x[1]w[2]+x[2]w[1]+x[3]w[0]$
这里假设 $x$和 $w$都是从 $0$开始的,并且 $x$和 $w$都能取到 $x[3]$和 $w[3]$。

  当然对于不是从 $0$开始的也成立，假设 $x$是从 $-1$开始的， $w$是从 $0$开始的，那么

$y[2]=x[-1]w[3]+x[0]w[2]+x[1]w[1]+x[2]w[0]$
上述表达式成立前提是 $x$有 $x[2]$和 $w$有 $w[3]$。

有限长序列卷积

卷积后的长度

  假设序列 $x[n]$的有值区间为 $N_1\leq n \leq N_2$，长度为 $N=N_2-N_1+1$， $w[n]$的有值区间为 $N_3 \leq n \leq N_4$，长度为 $W=N_4-N_3+1$， $y[n]=x[n]*w[n]$，那么 $y[n]$的长度是多少，有值区间又是多少？

  从卷积的表示式得到 $y[n]=\sum_{m=-\infty}^{\infty} x[m]w[n-m]$
所以
$N_1 \leq m \leq N_2 \\ N_3 \leq n-m \leq N_4$
得到
$N_1+N_3 \leq n \leq N_2+N_4$
所以 $y[n]$的长度为
$\begin{aligned} &N_2+N_4-(N_1+N_3)+1\\ &=(N_2-N_1+1)+(N_4-N_3+1)-1 \\ &=N+ M -1 \end{aligned}$
有值区间为
$N_1+N_3 \leq n \leq N_2+N_4$

  所以得到的结论是，两有限长序列的卷积，卷积后序列长度为两序列长度相加再减一，卷积序列有值区间的起点为两序列的起点相加，终点为两序列的终点相加。

  在这里给出一个卷积和计算的例子(用计算机实现的)

卷积和 $y[n]=x[n]*w[n]$

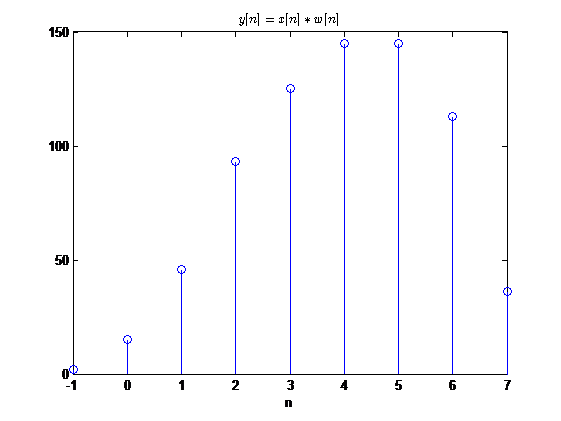
  观察到卷积后序列的有值区间的起点为序列起点的相加 $-2+1=-1$，终点为两序列终点的相加 $3+4=7$

用多项式乘法快速计算卷积

  该方法在有的书上也叫作列表法，不过我觉得叫什么无所谓，能掌握怎么计算的就可以
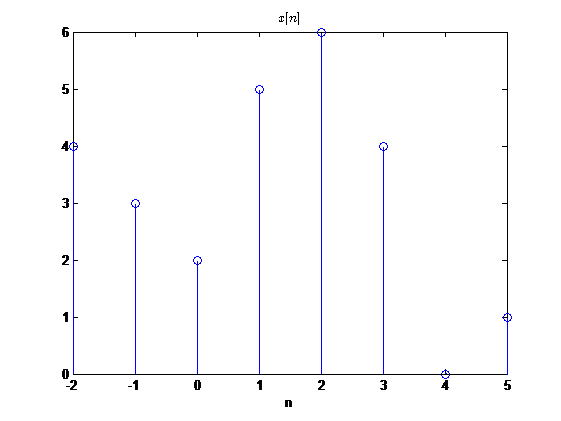
我们就用上图中的例子为例：
$x[n]=\{1 ,5,\mathop{6}\limits_{\uparrow}, 7, 8, 9\}$
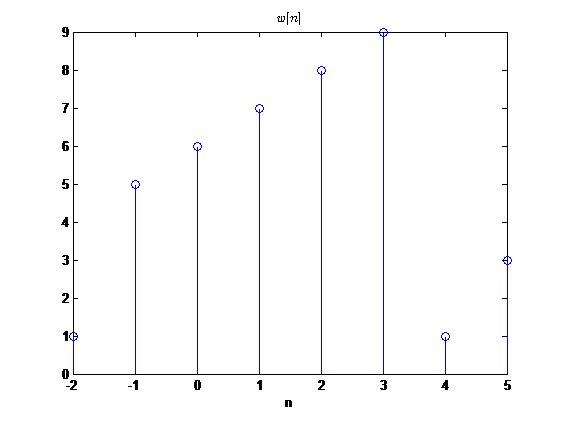
$w[n]=\{2,5,9,4\} \quad w[n]从1开始$
  我们先用定义法计算，首先我们可以得到 $y[n]$的有值区间为 $[-1,7]$，然后利用介绍的快速展开计算每一项的值：
$\begin{aligned} y[-1]&=x[-2]w[1]=2 \\ y[0]&=x[-2]w[2]+x[-1]w[1]=1*5+5*2=15 \\ y[1]&=x[-2]w[3]+x[-1]w[2]+x[0]w[1]=1*9+5*5+6*2=46\\ y[2]&=x[-2]w[4]+x[-1]w[3]+x[0]w[2]+x[1]w[1]=1*4+5*9+6*5+7*2=93\\ y[3]&=x[-1]w[4]+x[0]w[3]+x[1]w[2]+x[2]w[1]=5*4+6*9+7*5+8*2=125\\ y[4]&=x[0]w[4]+x[1]w[3]+x[2]w[2]+x[3]w[1]=6*4+7*9+8*5+9*2=145\\ y[5]&=x[1]w[4]+x[2]w[2]+x[3]w[1]=7*4+8*9+9*5=145\\ y[6]&=x[2]w[4]+x[3]w[3]=8*4+9*9=113\\ y[7]&=x[3]w[4]=9*4=36 \end{aligned}$

  得到的结果应该与上图中的 $y[n]$是相同的，但是说实话，做完这一遍我再也不想做第二遍，在这里介绍第二种快速计算的方法，这种方法手算比前面的快很多倍，只要会乘法就可以。

  还是以以上的 $x[n]$和 $w[n]$为例，将 $x[n]$和 $w[n]$列出来，如下所示

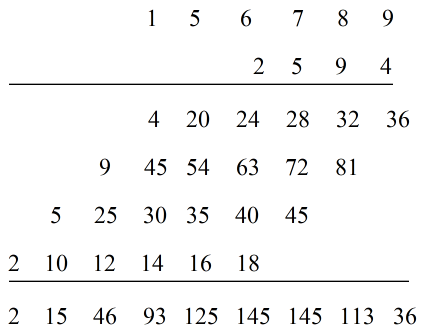
  按照多项式乘法的规则即可，不过与多项式乘法不同的是，不用逢十进位，通过这个方法得到的序列是
$y[n]=\{2,15,46,93,125,145,145,113,36\}$

  与上面用定义计算得到的结果是一样的，但是我这里没有标出 $0$的位置，如何快速得出 $y[0]$的位置呢(虽然我们知道 $y[n]$的起始位置是 $-1$，可以推出 $0$的位置)，那就是用小数乘法，将0位置后面标出小数点，比如序列 $x[n]$在 $x[0]=6$的后面标一个小数点，w可以在前面补0，所以可以写成

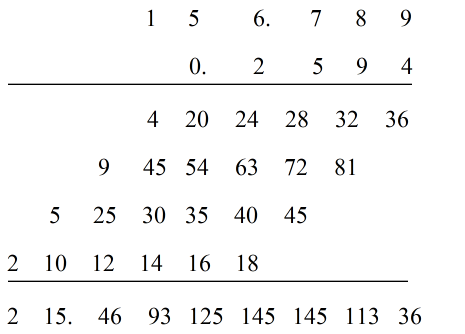
所以 $15$就是 $y[0]$的位置。

  至于多项式乘法为什么可以计算卷积，感兴趣的可以自己去查阅资料，毕竟这不是重点，重点是大家掌握这种方法就可以。

  其实卷积还有很多有意思的性质，大家可以在习题中多多体会，这里贴出我写的配套习题，因为刚写还在完善，所以不全，这个习题是我参考教材

数字信号处理----基于计算机的方法

离散时间信号与系统题目

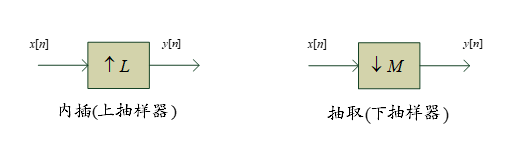
抽样率转换

  从一个序列生成抽样率高于或低于它的序列叫做抽样率转换。

  假设 $x[n]$是以频率 $F_THz$抽样得到的序列，由 $x[n]$得到的 $y[n]$的序列抽样频率为 $F^{'}_THz$，定义抽样率转换比
$\frac{F^{'}_T}{F_T}=R$
如果 $R>1$，也就是说 $F^{'}_T > F_T$，得到的抽样频率变大了，由 $x[n]$得到抽样频率更大的 $y[n]$的运算叫做内插，实现该运算的叫做内插器。反之如果得到的抽样频率更小，那么该运算叫做抽取，相应实现该运算的叫做抽取器。

  那么为什么叫做内插和抽取呢？到底内插和抽取是怎么样的一个过程。

  假设序列 $x[n]$是以频率 $F_T$对信号进行抽样，而另一个信号 $y[n]$的抽样频率 $F^{'}_T$是 $x[n]$的两倍，那么这就意味着 $y[n]$的样本值的个数是 $x[n]$的两倍，所以从 $x[n]$得到 $y[n]$就得"插入"多余的那些样本值，一般插入的都是0。假设 $F_T^{'}=2F_T$，那么 $x[n]$就得每隔一点插入一个0。

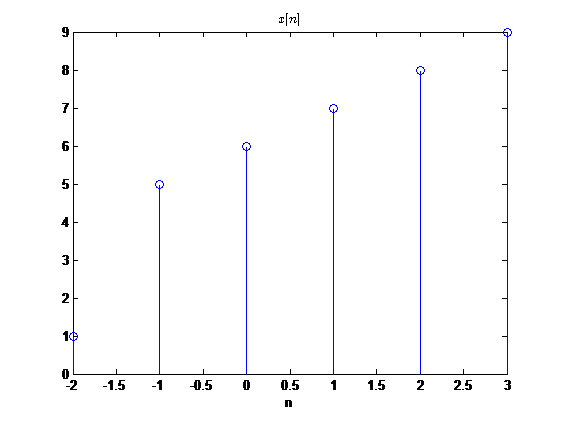
  我以一个例子来说明内插是一个什么样的过程，假设 $F_T^{'}=2F_T$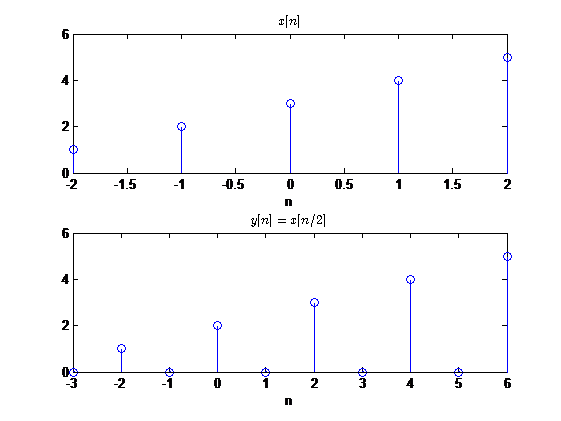

  一般的如果 $F^{'}_T=LF_T,L>1$，那么 $y[n]$与 $x[n]$之间的关系为
$y[n]= \begin{cases} x[n/L],\quad &n=0,\pm L, \pm 2L, ...\\ 0,\quad&其他 \end{cases}$

  相反，如果得到序列的抽样频率更低的话，也就是说 $x[n]$的样本值个数更多，就得减少 $x[n]$的个数，具体的做法就是抽取，如果 $F_T=2F^{'}_T$的话，那么就每隔一个抽取一个样本值。

  同样以一个例子演示抽取的过程：

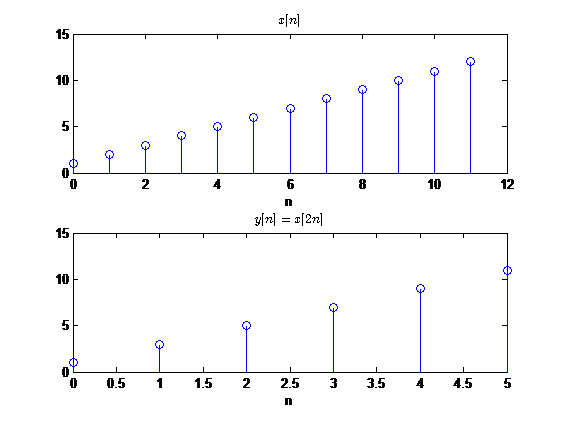
  一般的如果 $F_T=MF_T^{'},M>1$，那么 $y[n]$与 $x[n]$之间的关系为
$y[n]=x[nM]$