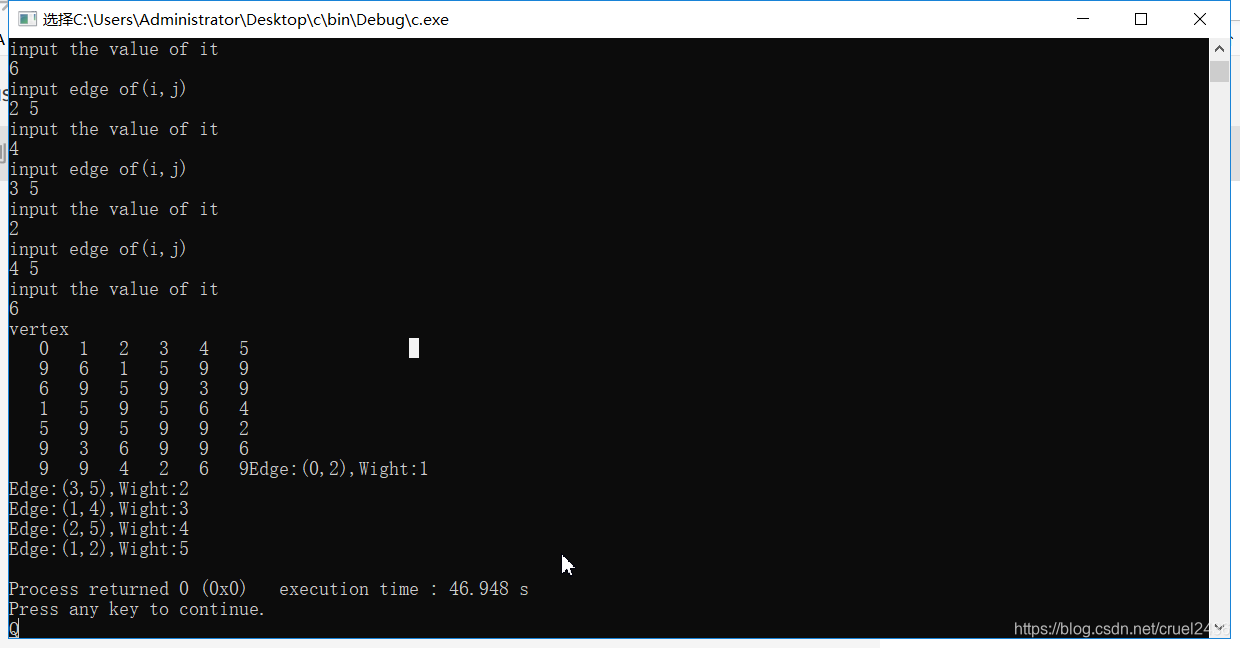
代码如下:
#include <stdio.h>
#include <stdlib.h>
#define MAXSIZE 100
typedef struct
{
int u;
int v;
int w;
}Edges;
void Bubblesort(Edges R[],int e)//e代表边的数量
{
Edges temp;
int i,j,swap;
for(i=0;i<e-1;i++)
{
swap=0;
for(j=0;j<e-i-1;j++)
if(R[j].w>R[j+1].w)
{
temp=R[j];
R[j]=R[j+1];
R[j+1]=temp;
swap=1;
}
if(swap==0)break;//冒泡排序对的优化,若本趟未出现排序则结束
}
}
typedef struct
{
int vertex[MAXSIZE];
int edges[MAXSIZE][MAXSIZE];
}Graph;
void creatGraph(Graph *p)
{
int n,e,i,j,k,x;
printf(“print the number of vertex\n”);
scanf("%d",&n);
// printf(“input data of vertex\n”);
for(i=0;i<n;i++)//初始化顶点信息
{
//scanf("%d",&j);
//p->vertex[i]=j;
p->vertex[i]=i;
}
for(i=0;i<n;i++)//初始化边关系
for(j=0;j<n;j++)
p->edges[i][j]=9;//设9为极大值
printf("print the number of edges\n");
scanf("%d",&e);
for(k=0;k<e;k++)
{
printf("input edge of(i,j)\n");
scanf("%d%d",&i,&j);
printf("input the value of it\n");
scanf("%d",&x);
p->edges[i][j]=x;
p->edges[j][i]=x;
}
}
void showGraph(Graph *p,int n)
{
int i,j;
printf(“vertex\n”);
for(i=0;i<n;i++)
printf("%4d",p->vertex[i]);
for(i=0;i<n;i++)
{
printf("\n");
for(j=0;j<n;j++)
printf("%4d",p->edges[i][j]);
}
printf("\n");
}
void Kruskal(int gm[][MAXSIZE],int n)
{
//n为顶点个数
int i,j,u1,v1,sn1,sn2,k;
int vest[MAXSIZE];
Edges E[MAXSIZE];
k=0;
for(i=0;i<n;i++)
for(j=0;j<n;j++)
if(i<j&&gm[i][j]!=9)//前面设9为极大值
{
E[k].u=i;
E[k].v=j;
E[k].w=gm[i][j];
k++;
}
Bubblesort(E,k);
for(i=0;i<n;i++)//初始化辅助数组,给每个顶点置不同连通分量
vest[i]=i;
k=1;//k表是当前构造生成树的第几条边,初值为1
j=0;//j为E中元素下标,初值为1
while(k<n)//产生n-条边
{
u1=E[j].u;
v1=E[j].v;
sn1=vest[u1];
sn2=vest[v1];
if(sn1!=sn2)
{
printf(“Edge:(%d,%d),Wight:%d\n”,u1,v1,E[j].w);
k++;
for(i=0;i<n;i++)//统一编号
if(vest[i]==sn2)
vest[i]=sn1;
}
j++;//扫描下一条边
}
}
int main()
{
Graph M,*p=&M;
creatGraph§;
showGraph(p,6);
Kruskal(&(p->edges[0]),6);
return 0;
}