Arthur Samuel (1959)定义机器学习为:不用明确编程,给予计算机学习能力的领域(Machine Learning: Field of
Tom Mitchell (1998)定义机器学习为:使计算机从经验E学习任务T达到性能度量P,当且仅当,有了经验E,经过P评判,提高解决任务T的性能(A computer program is said to learn from experience E with respect to some task T and some performance measure P, if its performance on T, as measured by P, improves with experience E.)
给定正确的数据进行学习,比如给定若干房屋面积x和房屋价格y的对应离散值(x,y)作为经验E,预测某个房屋面积下对应的房价(任务T),而预测成功的概率则是P。
包括回归问题和分类问题
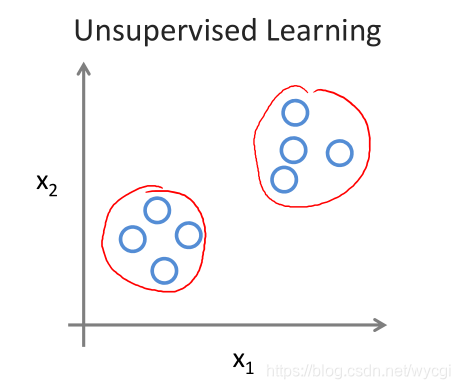
给定数据集,一般研究数据的聚集,如下图所示的圆圈,即是各种数据。
一般应用于大型计算机集群、网络集群分析、市场领域分割和天文数据分析。
分为聚类算法和非聚类算法(鸡尾酒会算法),如上图就是聚类,非聚类的意思就是指在混乱的数据中寻找结构(比如在嘈杂的酒会录音中分离出每个人的声音)
预设参数
假设h
h
θ
(
x
)
=
θ
0
+
θ
1
x
h_\theta(x)=\theta_0+\theta_1x
h θ ( x ) = θ 0 + θ 1 x
θ
0
\theta_0
θ 0
θ
1
\theta_1
θ 1
代价函数J
J
(
θ
0
,
θ
1
)
=
1
2
m
∑
i
=
1
m
(
h
θ
(
x
(
i
)
)
−
y
(
i
)
)
J(\theta_0,\theta_1)=\frac{1}{2m}\sum_{i=1}^m (h_\theta(x^{(i)})-y^{(i)})
J ( θ 0 , θ 1 ) = 2 m 1 i = 1 ∑ m ( h θ ( x ( i ) ) − y ( i ) )
x
(
i
)
x^{(i)}
x ( i )
y
(
i
)
y^{(i)}
y ( i )
(
x
(
i
)
,
y
(
i
)
)
(x^{(i)},y^{(i)})
( x ( i ) , y ( i ) )
目标函数
θ
0
\theta_0
θ 0
θ
1
\theta_1
θ 1
min
J
(
θ
0
,
θ
1
)
\min J(\theta_0,\theta_1)
min J ( θ 0 , θ 1 )
梯度下降算法
(
θ
0
,
θ
1
)
(\theta_0,\theta_1)
( θ 0 , θ 1 )
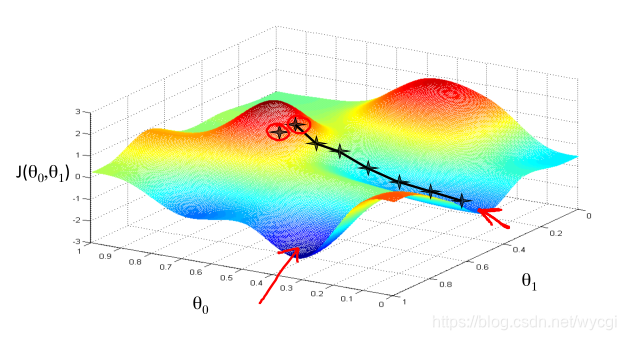
但是,如下图可知,有可能因参数值不同,使得下降路线不同,换句话说,一次只能找到局部最优值。
算法形式表示为:
θ
j
:
=
θ
j
−
α
∂
∂
θ
j
J
(
θ
0
,
θ
1
)
(
f
o
r
j
=
0
a
n
d
j
=
1
)
\theta_j:=\theta_j-\alpha\frac{\partial}{\partial\theta_j}J(\theta_0,\theta_1)\quad(for\quad j=0\quad and \quad j=1)
θ j : = θ j − α ∂ θ j ∂ J ( θ 0 , θ 1 ) ( f o r j = 0 a n d j = 1 )
α
\alpha
α
∂
∂
θ
j
J
(
θ
0
,
θ
1
)
\frac{\partial}{\partial\theta_j}J(\theta_0,\theta_1)
∂ θ j ∂ J ( θ 0 , θ 1 )
重点:正确的更新形式是同时更新
θ
0
\theta_0
θ 0
θ
1
\theta_1
θ 1 ,具体如下:
t
e
m
p
0
:
=
θ
0
−
α
∂
∂
θ
0
J
(
θ
0
,
θ
1
)
t
e
m
p
1
:
=
θ
1
−
α
∂
∂
θ
1
J
(
θ
0
,
θ
1
)
θ
0
=
t
e
m
p
0
θ
1
=
t
e
m
p
1
temp0:=\theta_0-\alpha\frac{\partial}{\partial\theta_0}J(\theta_0,\theta_1)\\ temp1:=\theta_1-\alpha\frac{\partial}{\partial\theta_1}J(\theta_0,\theta_1)\\ \theta_0=temp0\\ \theta_1=temp1
t e m p 0 : = θ 0 − α ∂ θ 0 ∂ J ( θ 0 , θ 1 ) t e m p 1 : = θ 1 − α ∂ θ 1 ∂ J ( θ 0 , θ 1 ) θ 0 = t e m p 0 θ 1 = t e m p 1
t
e
m
p
0
:
=
θ
0
−
α
∂
∂
θ
0
J
(
θ
0
,
θ
1
)
θ
0
=
t
e
m
p
0
t
e
m
p
1
:
=
θ
1
−
α
∂
∂
θ
1
J
(
θ
0
,
θ
1
)
θ
1
=
t
e
m
p
1
temp0:=\theta_0-\alpha\frac{\partial}{\partial\theta_0}J(\theta_0,\theta_1)\\ \theta_0=temp0\\ temp1:=\theta_1-\alpha\frac{\partial}{\partial\theta_1}J(\theta_0,\theta_1)\\ \theta_1=temp1
t e m p 0 : = θ 0 − α ∂ θ 0 ∂ J ( θ 0 , θ 1 ) θ 0 = t e m p 0 t e m p 1 : = θ 1 − α ∂ θ 1 ∂ J ( θ 0 , θ 1 ) θ 1 = t e m p 1
最终通过梯度下降算法,得到使
J
(
θ
0
,
θ
1
)
=
0
J(\theta_0,\theta_1)=0
J ( θ 0 , θ 1 ) = 0
(
θ
0
,
θ
1
)
(\theta_0,\theta_1)
( θ 0 , θ 1 )
矩阵表示为:
矩
阵
A
=
[
a
b
c
d
]
矩阵A= \begin{bmatrix} a & b \\ c & d \end{bmatrix}
矩 阵 A = [ a c b d ]
A
i
j
A_{ij}
A i j
A
m
n
A^{mn}
A m n
向量表示为:
三
维
向
量
y
=
[
a
b
c
]
三维向量y= \begin{bmatrix} a \\ b \\ c \\ \end{bmatrix}
三 维 向 量 y = ⎣ ⎡ a b c ⎦ ⎤
y
i
y_i
y i
矩阵的加法、乘法
矩阵的加法是每个对应的元素直接相加,具体如下:
[
1
2
3
4
]
+
[
1
2
1
2
]
=
[
1
+
1
2
+
2
3
+
1
4
+
2
]
\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}+ \begin{bmatrix} 1 & 2 \\ 1 & 2 \end{bmatrix}= \begin{bmatrix} 1+1 & 2+2 \\ 3+1 & 4+2 \end{bmatrix}
[ 1 3 2 4 ] + [ 1 1 2 2 ] = [ 1 + 1 3 + 1 2 + 2 4 + 2 ]
矩阵的乘法分为标量乘法和矩阵间相乘
3
∗
[
1
2
3
4
]
=
[
3
∗
1
3
∗
2
3
∗
3
3
∗
4
]
3* \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}= \begin{bmatrix} 3*1 & 3*2 \\ 3*3 & 3*4 \end{bmatrix}
3 ∗ [ 1 3 2 4 ] = [ 3 ∗ 1 3 ∗ 3 3 ∗ 2 3 ∗ 4 ]
[
1
2
3
3
4
5
]
∗
[
1
0
2
1
0
1
]
\begin{bmatrix} 1 & 2 & 3\\ 3 & 4 & 5 \end{bmatrix}* \begin{bmatrix} 1 & 0 \\ 2 & 1 \\ 0 & 1 \end{bmatrix}
[ 1 3 2 4 3 5 ] ∗ ⎣ ⎡ 1 2 0 0 1 1 ⎦ ⎤
[
1
2
3
3
4
5
]
∗
[
1
2
0
]
=
[
1
∗
1
+
2
∗
2
+
3
∗
0
3
∗
1
+
4
∗
2
+
5
∗
0
]
(
1
)
\begin{bmatrix} 1 & 2 & 3\\ 3 & 4 & 5 \end{bmatrix}* \begin{bmatrix} 1 \\ 2 \\ 0 \end{bmatrix}= \begin{bmatrix} 1*1+2*2+3*0 \\ 3*1+4*2+5*0 \end{bmatrix}(1)
[ 1 3 2 4 3 5 ] ∗ ⎣ ⎡ 1 2 0 ⎦ ⎤ = [ 1 ∗ 1 + 2 ∗ 2 + 3 ∗ 0 3 ∗ 1 + 4 ∗ 2 + 5 ∗ 0 ] ( 1 )
[
1
2
3
3
4
5
]
∗
[
0
1
1
]
=
[
1
∗
0
+
2
∗
1
+
3
∗
1
3
∗
0
+
4
∗
1
+
5
∗
1
]
(
2
)
\begin{bmatrix} 1 & 2 & 3\\ 3 & 4 & 5 \end{bmatrix}* \begin{bmatrix} 0 \\ 1 \\ 1 \end{bmatrix}= \begin{bmatrix} 1*0+2*1+3*1 \\ 3*0+4*1+5*1 \end{bmatrix}(2)
[ 1 3 2 4 3 5 ] ∗ ⎣ ⎡ 0 1 1 ⎦ ⎤ = [ 1 ∗ 0 + 2 ∗ 1 + 3 ∗ 1 3 ∗ 0 + 4 ∗ 1 + 5 ∗ 1 ] ( 2 )
乘法的运算性质
̸
=
\not=
̸ =
octave中,矩阵的代码为:A=[1, 2, 3; 4, 5, 6]。
逆矩阵
A
−
1
A^{-1}
A − 1
A
A
−
1
=
A
−
1
A
=
I
AA^{-1}=A^{-1}A=I
A A − 1 = A − 1 A = I
A
−
1
A^{-1}
A − 1
A
A
A
伪逆矩阵
B
B
B
A
⋅
B
⋅
A
=
A
B
⋅
A
⋅
B
=
B
A\cdot B\cdot A=A\\ B\cdot A\cdot B=B
A ⋅ B ⋅ A = A B ⋅ A ⋅ B = B
B
B
B
A
A
A
octave中,求伪逆矩阵的代码为pinv(A);求逆矩阵的代码为inv(A)。
转置矩阵
A
T
A^T
A T
A
=
[
1
2
3
3
4
5
]
A
T
=
[
1
3
2
4
3
5
]
A=\begin{bmatrix} 1 & 2 & 3\\ 3 & 4 & 5 \end{bmatrix} \\ A^T=\begin{bmatrix} 1 & 3 \\ 2 & 4 \\ 3 & 5 \end{bmatrix}
A = [ 1 3 2 4 3 5 ] A T = ⎣ ⎡ 1 2 3 3 4 5 ⎦ ⎤
A
i
j
=
A
j
i
T
A_{ij}=A^T_{ji}
A i j = A j i T
octave中,
A
A
A
A
′
A'
A ′