题意翻译
题目大意：给定一个无向图，定义一个图的联通导出子图的密度为其点权之和除以边权之和。（注：边权之和为零的图密度为零）求该图的联通导出子图的最大密度。一个图的导出子图是指，选取一个顶点集，以两端点均在该顶点集中的边的全体为边集的子图。
输入格式：第一行两个整数n (1<=n<=500) ,m(0<=m<=n(n-1)/2)，分别表示图的节点数和边数。第二行n个整数xi（1<=xi<=1000000）表示第i个点的权值。后m行每行三个整数ai,bi,ci，(1<=ai,bi<=n;1<=ci<=1000)表示从ai到bi有一条权值为ci的无向边。数据保证无重边。
输出：一个浮点数，表示该图的联通导出子图密度的最大值，保留小数点后15位。如果你的答案和标准答案相差不超过10e-9，则被认为是正确的。
题目描述
DZY loves Physics, and he enjoys calculating density.
Almost everything has density, even a graph. We define the density of a non-directed graph (nodes and edges of the graph have some values) as follows:
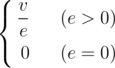where v v v is the sum of the values of the nodes, e e e is the sum of the values of the edges.Once DZY got a graph G G G , now he wants to find a connected induced subgraph G′ G' G′ of the graph, such that the density of G′ G' G′ is as large as possible.
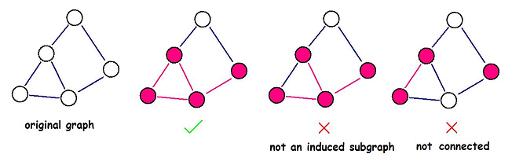
An induced subgraph G′(V′,E′) G'(V',E') G′(V′,E′) of a graph G(V,E) G(V,E) G(V,E) is a graph that satisfies:
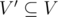;- edge
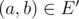if and only if 
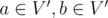, and edge 
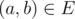; - the value of an edge in G′ G' G′ is the same as the value of the corresponding edge in G G G , so as the value of a node.
Help DZY to find the induced subgraph with maximum density. Note that the induced subgraph you choose must be connected.
输入输出格式
输入格式：
The first line contains two space-separated integers $ n (1<=n<=500) $ ,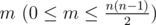 
. Integer n n n represents the number of nodes of the graph G G G , m m m represents the number of edges.
The second line contains n n n space-separated integers $ x_{i} (1<=x_{i}<=10^{6}) $ , where xi x_{i} xi represents the value of the i i i -th node. Consider the graph nodes are numbered from 1 1 1 to n n n .
Each of the next m m m lines contains three space-separated integers $ a_{i},b_{i},c_{i} (1<=a_{i}<b_{i}<=n; 1<=c_{i}<=10^{3}) $ , denoting an edge between node ai a_{i} ai and bi b_{i} bi with value ci c_{i} ci . The graph won't contain multiple edges.
输出格式：
Output a real number denoting the answer, with an absolute or relative error of at most 10−9 10^{-9} 10−9 .
输入输出样例
输入样例#1： 复制
1 0 1
输出样例#1： 复制
0.000000000000000
输入样例#2： 复制
2 1 1 2 1 2 1
输出样例#2： 复制
3.000000000000000
输入样例#3： 复制
5 6 13 56 73 98 17 1 2 56 1 3 29 1 4 42 2 3 95 2 4 88 3 4 63
输出样例#3： 复制
2.965517241379311
说明
In the first sample, you can only choose an empty subgraph, or the subgraph containing only node 1 1 1 .
In the second sample, choosing the whole graph is optimal.
我们可以证明一定是选取一条边时最优；
证明：
假设不是选取一条边时最优，
那么此时最优解为 ansV>2 ,ansE>1;
密度 ans=ansV/ansE;
那么对于该导出子图中的边，一定有： (u+v)/w< ans;
即 ： u+v< w*ans;
其中 w 为边的权值，对边求和累加：
而 ansE=
即得出 , 矛盾，得证；
所以枚举边即可解决；
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstdlib>
#include<cstring>
#include<string>
#include<cmath>
#include<map>
#include<set>
#include<vector>
#include<queue>
#include<bitset>
#include<ctime>
#include<deque>
#include<stack>
#include<functional>
#include<sstream>
//#include<cctype>
//#pragma GCC optimize("O3")
using namespace std;
#define maxn 100005
#define inf 0x3f3f3f3f
#define INF 999999999999999
#define rdint(x) scanf("%d",&x)
#define rdllt(x) scanf("%lld",&x)
#define rdlf(x) scanf("%lf",&x)
#define rdstr(x) scanf("%s",x)
typedef long long ll;
typedef unsigned long long ull;
typedef unsigned int U;
#define ms(x) memset((x),0,sizeof(x))
const long long int mod = 1e9 + 7;
#define Mod 20100403
#define sq(x) (x)*(x)
#define eps 1e-3
typedef pair<int, int> pii;
#define pi acos(-1.0)
const int N = 1005;
#define REP(i,n) for(int i=0;i<(n);i++)
inline ll rd() {
ll x = 0;
char c = getchar();
bool f = false;
while (!isdigit(c)) {
if (c == '-') f = true;
c = getchar();
}
while (isdigit(c)) {
x = (x << 1) + (x << 3) + (c ^ 48);
c = getchar();
}
return f ? -x : x;
}
ll gcd(ll a, ll b) {
return b == 0 ? a : gcd(b, a%b);
}
ll sqr(ll x) { return x * x; }
int n, m;
int v[maxn];
int main()
{
//ios::sync_with_stdio(false);
rdint(n); rdint(m);
double Max = 0.0;
for (int i = 1; i <= n; i++)rdint(v[i]);
for (int i = 1; i <= m; i++) {
int x, y, z; rdint(x); rdint(y); rdint(z);
double tmp = 1.0*(v[x] + v[y]) / z;
Max = max(Max, tmp);
}
printf("%.15lf\n", Max);
return 0;
}