说实话题目不简单(虽然都没有超过noip的考试范围)
T2T3暴力非常的良心,再加上出题人给出了数据编号,变得更加的良心了........
所以最后的得分是非常好看的
T1
典型的“反悔”型的贪心问题。
记得当时第一次遇见推dp式子推了好久好久来着...........
最后发现并不需要dp的操作.........
我们可以首先观察这个问题的性质:
我们先在某一个位置买下一个物品,然后到另外一个位置卖掉它,而我们可以赚到中间的差价。
然后我们可以发现,对于单个物品来说,如果能够把它在价格最高的地方卖出去,肯定可以赚更多的钱,但是我们并不知道中间到底有多少个物品,这就使得中间并非价格最高的地方可能会存在更优的解,而我们像刚才那么贪心肯定是没有办法考虑完所有情况的。
那么我们现在就需要一种能够适应所有情况的方法。
我们发现,对于数据1 1 5 3 6来说,我们可以按照如下的过程完成它:
首先遇到一个1,我们先把它放置在原处,并且加入一个堆(小根堆)中
遇到第二个1,我们发现就算在之前买下第一个1并且在这里卖出也赚不了钱,也加入堆中。
遇到5,我们发现堆中的最小元素1比它要更小,那么我们考虑买之前的1并且在5这里卖出,这样的话能获得4的收益,而第一个1已经被我们所购买,鉴于每个物品只能买卖一次,我们是无法卖出它的,所以说我们需要将这一个1pop掉,从堆中删除。
遇到3,我们发现堆中还剩余一个最小值1,那么重复我们遇到5时的步骤,我们在之前买1并在3这里卖掉,同时获得这次的2点收益。
遇到6,我们可以一眼发现,之前的1肯定是在6卖出是最优的而不是在这一个3的位置取得最优解,所以我们需要考虑解决这个情况的方法。
我们还可以发现,我们在6的位置卖掉之前的1,与我们先在3的位置卖掉1,随后又在6的位置卖掉3(相当于反悔了,我们不卖之前的3,而选择卖这个6,那么我们所赚取的利益就相当于是先赚取了3的利益,然后又赚取了6对3的利益)
如果从这么看来,那么我们每一次都将当前元素压进堆中就好了。
但是这样并不对,我们需要注意题目中的条件:
限制在买、离开、 卖中三选一,这句话是什么意思呢
我们每一次压进堆里的东西都会有两种可能,第一种是我们把它放置在原处等待后面的物品是否又能够将其卖出并获得利益的
第二种则是我们已经卖掉的,观察后来能否通过反悔来赚取差价的物品。
但是任意一个物品在当前的操作中,只能三选一,所以你不能两头都占了....
因为已经卖掉的物品(后来反悔要用的物品),是不能再在后来买进的,所以这样考虑出来的贡献是会漏掉情况的,最后的答案会比标准答案要小的......
但是稍微再想想,既然没有办法解决重复的问题,那么我们直接开两个堆,一个维护卖掉反悔的,另外一个维护以后可能会卖掉的,每次比较卖出的价值就在两者中去最小值,每次反悔了就把反悔掉的物品再压回以后可能卖掉的物品的堆里面,就好了
#include<cstdio>
#include<queue>
#define OP "trade"
#define LL long long
inline char nc()
{
static char buf[100000],*p1=buf,*p2=buf;
return p1==p2&&(p2=(p1=buf)+fread(buf,1,100000,stdin),p1==p2)?EOF:*p1++;
}
inline void read(int &x)
{
char c=nc(),b=1;
for (;!(c>='0' && c<='9');c=nc()) if (c=='-') b=-1;
for (x=0;c>='0' && c<='9';x=x*10+c-'0',c=nc()); x*=b;
}
const int MAXN=1e5+5;
const int INF=1e9+7;
int a[MAXN];
LL ans=0;
class Node
{
public:
int val;
bool operator <(const Node &z)const
{
return val>z.val;
}
};
std::priority_queue<Node>q1;
std::priority_queue<Node>q2;
int main()
{
std::freopen(OP".in","r",stdin);
std::freopen(OP".out","w",stdout);
int n;
read(n);
for(int i=1;i<=n;i++)
{
read(a[i]);
}
q2.push((Node){INF});
q1.push((Node){INF});
for(int i=1;i<=n;i++)
{
Node p1=q1.top();
Node p2=q2.top();
if(p1.val<p2.val)
{
if(a[i]>p1.val)
{
ans+=1ll*a[i]-p1.val;
q2.push((Node){a[i]});
q1.pop();
}
else
{
q1.push((Node){a[i]});
}
}
else
{
if(a[i]>p2.val)
{
ans+=1ll*a[i]-p2.val;
q2.push((Node){a[i]});
q2.pop();
q1.push((Node){p2.val});
}
else
{
q1.push((Node){a[i]});
}
}
}
std::printf("%lld\n",ans);
return 0;
}总而言之很快就切掉了啦.......
T2
虽然正解并不是非常复杂但是也不太好想
但是暴力分真的太良心了.........
这个出题人如果是妹子我一定要娶她2333333(输入测试点编号简直让人感到泪目。。。。。)
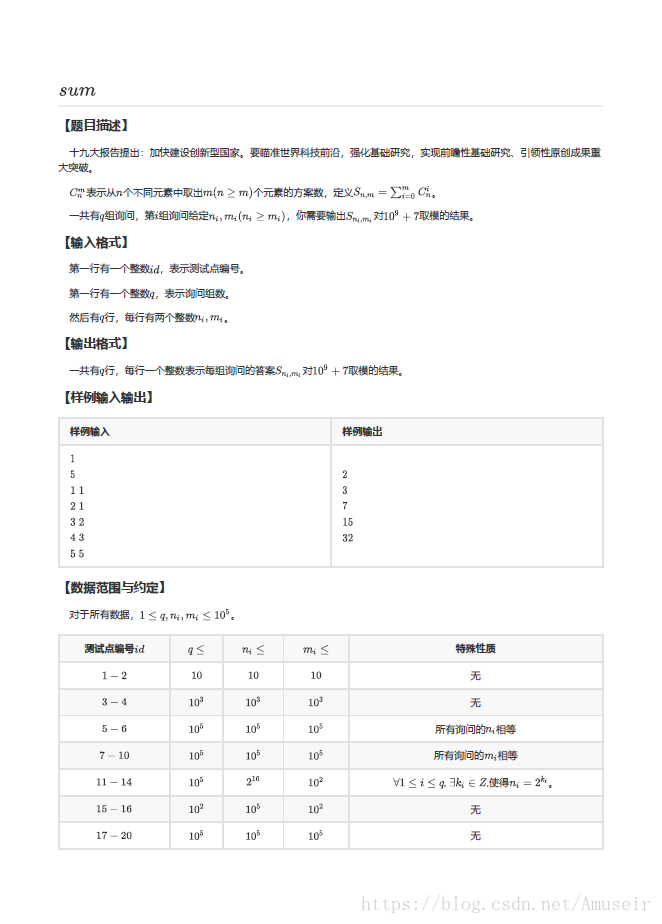
我们可以通过打表/手推的方式轻松地得到其大概意义上的两个公式
S(n,m)=S(n,m-1)+C(n,m);(这个其实是废话来着.....)
S(n,m)=2*S(n-1,m)-C(n-1,m)(所以说题目中的那30分的特殊数据就是用来启发我们思考正解的)
我们发现
如果我们知道了S(n,m)
那么我们可以通过预处理阶乘和逆元的方式O(1)求得组合数
然后O(1)求出:
S(n,m-1)
S(n-1,m)
S(n+1,m)
S(n,m+1);
然后我们将m、n换成l、r。
发现m严格小于n
再结合上面的式子看看
嗯........熟悉的感觉
对!不知道你发现没有,知道这个规律好像可以莫队诶~!!!!!(233333反正我是没看出来的,不知道出题人脑洞怎么这么大........)
知道当前区间答案,可以O(1)推出区间左右端点移动以后的答案,还可以O(1)出公式,那么我们就可以考虑使用莫队算法
然后这道题就变成了莫队算法的裸题..................
拍拍板子就过了(考场上只有一个人想到了分块的做法....然后我们都苟住了良心的50、60分暴力)
#include<cmath>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define LL long long
#define OP "sum"
inline char nc()
{
static char buf[100000],*p1=buf,*p2=buf;
return p1==p2&&(p2=(p1=buf)+fread(buf,1,100000,stdin),p1==p2)?EOF:*p1++;
}
inline void read(int &x)
{
char c=nc(),b=1;
for (;!(c>='0' && c<='9');c=nc()) if (c=='-') b=-1;
for (x=0;c>='0' && c<='9';x=x*10+c-'0',c=nc()); x*=b;
}
const int MAXN=1e5+5;
const int MOD=1e9+7;
class Query
{
public:
int l;
int r;
int color;
int id;
bool operator <(const Query &z)const
{
if(color==z.color)
{
return r<z.r;
}
return color<z.color;
}
}q[MAXN];
LL fac[MAXN];
LL inv[MAXN];
void exgcd(int a,int b,LL &x,LL &y)
{
if(!b)
{
x=1;
y=0;
return;
}
else
{
exgcd(b,a%b,y,x);
y-=(a/b)*x;
}
}
LL inverse(int a,const int MOD)
{
LL x,y;
exgcd(a,MOD,x,y);
return (x%MOD+MOD)%MOD;
}
void init()
{
fac[0]=1;
for(int i=1;i<=100000;i++)
{
fac[i]=1ll*fac[i-1]*i%MOD;
}
inv[100000]=inverse(fac[100000],MOD);
inv[0]=1;
for(int i=100000-1;i>=1;i--)
{
inv[i]=inv[i+1]*(i+1)%MOD;
}
}
LL C(int n,int m)
{
return fac[n]*inv[m]%MOD*inv[n-m]%MOD;
}
int k;
LL ans[MAXN];
int main()
{
std::freopen(OP".in","r",stdin);
std::freopen(OP".out","w",stdout);
int id;
read(id);
read(k);
init();
for(int i=1;i<=k;i++)
{
int n,m;
read(n);
read(m);
q[i]=(Query){m,n,(m-1)/300+1,i};
}
std::sort(q+1,q+1+k);
LL sum=0;
int m=q[1].l;
int n=q[1].r;
for(int i=0;i<=m;i++)
{
sum=(sum+C(n,i)%MOD)%MOD;
}
ans[q[1].id]=sum;
for(int i=2;i<=k;i++)
{
while(m>q[i].l)
{
sum=(sum-C(n,m)+MOD)%MOD;
m--;
}
while(n<q[i].r)
{
sum=(2ll*sum%MOD-C(n,m)+MOD)%MOD;
n++;
}
while(q[i].l>m)
{
m++;
sum=(1ll*sum+C(n,m))%MOD;
}
while(q[i].r<n)
{
n--;
sum=(sum%MOD+C(n,m)%MOD)*inv[2]%MOD;
}
ans[q[i].id]=sum;
}
for(int i=1;i<=k;i++)
{
std::printf("%lld\n",ans[i]);
}
return 0;
}
/*
1
5
1 1
2 1
3 2
4 3
5 5
*/ T3

这道题乍一看很难
但是思路其实很简单......
满分就是一个大暴力..........
总共的楼盘个数非常简单,随便记录一个前缀和就大家都会做了
重点是联通块个数。
......
每一个行、列排序以后直接对于每一个板子(就是单次的建筑计划)二分查找其联通块。
然后把这些联通块for一遍用并查集记录一下联通块个数的前缀和就过了
但是代码非常非常难调试...........
#pragma G++ optimize(2)
#pragma C++ optimize(2)
#pragma GCC optimize(2)
#include<cstdio>
#include<cstdlib>
#include<vector>
#include<cstring>
#include<algorithm>
#define LL long long
#define OP "building"
inline char nc()
{
static char buf[100000],*p1=buf,*p2=buf;
return p1==p2&&(p2=(p1=buf)+fread(buf,1,100000,stdin),p1==p2)?EOF:*p1++;
}
inline void read(int &x)
{
char c=nc(),b=1;
for (;!(c>='0' && c<='9');c=nc()) if (c=='-') b=-1;
for (x=0;c>='0' && c<='9';x=x*10+c-'0',c=nc()); x*=b;
}
const int MAXN=5e5+5;
class Info
{
public:
int lx;
int ly;
int rx;
int ry;
}Q[MAXN];
class Node
{
public:
int l;
int r;
int id;
bool operator <(const Node &z)const
{
if(l==z.l)
{
return r<z.r;
}
return l<z.l;
}
};
std::vector<std::pair<int ,int > >G[MAXN];
std::vector<Node>row[MAXN];
std::vector<Node>col[MAXN];
LL sumr[MAXN];
LL sumc[MAXN];
LL ans_num[MAXN];
LL ans_cnt[MAXN];
int f[MAXN];
int find(int x)
{
return x==f[x]?x:f[x]=find(f[x]);
}
int K=0;
void unionn(int u,int v)
{
if(find(u)!=find(v))
{
f[find(u)]=find(v);
K++;
}
}
int n,m,k,q;
void init()
{
read(n);
read(m);
read(k);
read(q);
for(int i=1;i<=k;i++)
{
int x1,y1,x2,y2;
read(x1);
read(y1);
read(x2);
read(y2);
if(x1==x2)
{
sumr[x1]+=(y2-y1+1);
}
else
{
sumc[x1]++;
sumc[x2+1]--;
}
Q[i]=(Info){x1,y1,x2,y2};
row[x1].push_back((Node){y1,y2,i});
col[y1].push_back((Node){x1,x2,i});
f[i]=i;
}
for(int i=1;i<=n;i++)
{
std::sort(row[i].begin(),row[i].end());
}
for(int i=1;i<=m;i++)
{
std::sort(col[i].begin(),col[i].end());
}
for(int i=1;i<=k;i++)
{
int r0=Q[i].rx+1;
int pos;
if(r0<=n&&row[r0].size())
{
pos=std::upper_bound(row[r0].begin(),row[r0].end(),(Node){Q[i].ry,m+1,0})-row[r0].begin()-1;
for(;pos>=0&&row[r0][pos].r>=Q[i].ly;pos--)
{
G[r0].push_back(std::make_pair(i,row[r0][pos].id));
}
}
int c0=Q[i].ry+1;
if(c0<=m&&col[c0].size())
{
pos=std::upper_bound(col[c0].begin(),col[c0].end(),(Node){Q[i].rx,n+1,0})-col[c0].begin()-1;
for(;pos>=0&&col[c0][pos].r>=Q[i].lx;pos--)
{
G[std::max(Q[i].lx,col[c0][pos].l)].push_back(std::make_pair(i,col[c0][pos].id));
}
}
}
for(int i=1;i<=n;i++)
{
sumc[i]+=sumc[i-1];
}
for(int i=1;i<=n;i++)
{
sumr[i]+=sumr[i-1];
sumc[i]+=sumc[i-1];
ans_num[i]=sumr[i]+sumc[i];
}
int tot=0;
for(int i=1;i<=n;i++)
{
tot+=row[i].size();
for(int j=0;j<(int)G[i].size();j++)
{
if(!G[i][j].first||!G[i][j].second)
{
exit(0);
}
else
{
unionn(G[i][j].first,G[i][j].second);
}
}
ans_cnt[i]=tot-K;
}
while(q--)
{
int opt,l;
read(opt);
read(l);
if(!opt)
{
std::printf("%lld\n",ans_num[l]);
}
else
{
std::printf("%lld\n",ans_cnt[l]);
}
}
}
int main()
{
std::freopen(OP".in","r",stdin);
std::freopen(OP".out","w",stdout);
int id;
read(id);
init();
return 0;
}