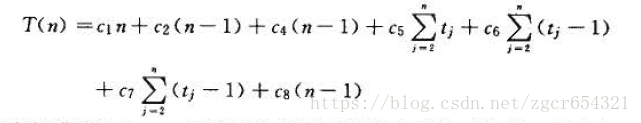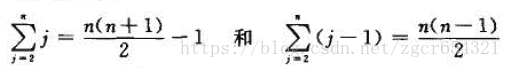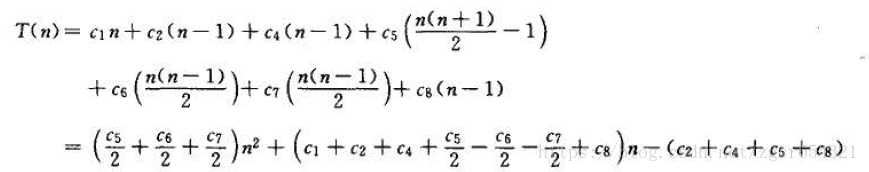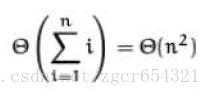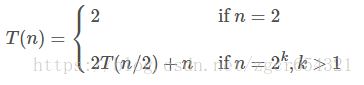插入排序：
排序问题的定义如下：
输入：N个数{a1, a2,..., an }。
输出：输入序列的一个排列{a'1 ,a'1 ,...,a'n }，使得a'n <=a' n<=...<=a' n。
待排序的数也称为关键字( key) 。
插入排序的伪代码为：
INSERTION-SORT
for j <- 2 to length[A]
key <- A[j]
Insert A[j]into the sorted sequence A[l...j-1].
i <- j - 1
while i > 0 and A[i] > key
A[i + 1] <- A[i]
i <- i - 1
A[i + 1] <- keyC/C++代码实现如下：
#include <stdio.h>
#include <string.h>
int main() {
int n;
int A[1000];
int k = 0;
while (scanf("%d", &n) != EOF) {
A[k] = n;
k++;
}
printf("input complete\n");
for (int j = 1; j < k; j++) {
int key = A[j];
int i = j - 1;
while (i >= 0 && A[i] > key) {
A[i + 1] = A[i];
i--;
}
A[i + 1] = key;
for (int i = 0; i < k; i++)
printf("%d ", A[i]);
printf("\n");
//打印每轮排序后的输出，这样看起来更清晰
}
printf("print the sorted number\n");
for (int i = 0; i < k; i++)
printf("%d ", A[i]);
return 0;
}运行结果如下：
8 7 9 2 4
^D
input complete
7 8 9 2 4
7 8 9 2 4
2 7 8 9 4
2 4 7 8 9
print the sorted number
2 4 7 8 9
Process finished with exit code 0python3代码实现如下：
A = []
while True:
try:
A.append(int(input()))
except:
print('input complete')
break
for j in range(len(A)):
if j >= 1:
key = A[j]
i = j - 1
while (i >= 0 and A[i] > key):
A[i + 1] = A[i]
i = i - 1
A[i + 1] = key
for i in range(len(A)):
print(A[i], end=' ')
print('\n', end='')
# 打印每轮排序后的输出，这样看起来更清晰
print('print the sorted number')
for i in range(len(A)):
print(A[i], end=' ')
# python3默认打印会换行，加上end=' '，则每次后面会自动加上' '中内容而不是换行运行结果如下：
8
7
5
9
2
^D
input complete
7 8 5 9 2
5 7 8 9 2
5 7 8 9 2
2 5 7 8 9
print the sorted number
2 5 7 8 9
Process finished with exit code 0循环不变式：
循环不变式主要用来帮助我们理解算法的正确性，对于循环不变式，必须具备三个性质：
初始化： 它在循环的第一轮迭代开始之前应该是正确的。
保持：如果在循环的某个一次迭代开始之前它是正确的，那么在下一次迭代开始之前，应该保持正确。
中止： 当循环结束时，不变式给出了一个有用的性质，它有助于表明算法是正确的。
当头两个性质成立时，就能保证循环不变式在循环的每一轮迭代开始之前，都是正确的。这类似于数学归纳法的证明。
在数学归纳法中，要证明某一性质是成立的，必须首先证明其基本情况和一个归纳步骤都是成立的。证明不变式在第一轮迭代开始之前是成立的，就有点类似千归纳法中对基本情况的证明；证明不变式在各次迭代之间保持成立， 就有点类似于归纳法中对归纳步骤的证明。
现在我们通过第一重循环的不变式来证明排序算法的正确性，循环不变式为：
（注意讨论循环不变式时数组下标认为从1开始）
A[1...j-1]是一个包含原数组第1到j-1元素并已排序的数组，A[j...n]A[j...n]是待排序数组。
初始化：
在第一轮循环体之前，j=2,那么A[j-1]只包含一个元素A[1]，A[1...j-1]显然有序，不变式成立；
保持：
A[1...j−1]是已排数组，通过内层循环（这里我们先不讨论第二重循环的不变式），A[j]被第j大的数交换，这就使得A[j]大于等于A[1...j−1]的所有数，小于等于A[j+1...n]的所有数。不变式仍然成立。
中止：
当循环中止时，假如i = 0，那么A[1]处是空值，A[2...j]有序，此时j=length[A]，且A[2...j]所有元素都大于key，那么将key放入A[1]将使A[1...j]有序；如果A[i]<=key，那么由于A[1...i]有序，所以key大于A[1...i]中所有元素，同时由于A[i+2,j]有序且所有元素都大于key，将key放入A[i+1]会使A[1...j]有序，不变式仍然成立。
循环中断的条件和不变式一起，可以证明算法的正确性。
我们再用循环不变式证明第二重while循环的正确性（注意分析时数组下标也认为是从1开始）：
第二重循环的目的找出一个值0<=i<=j，将key放入A[i+1]将使A[1...j]有序。这里我们可以认为当执行完"key<-A[j]"之后，A[j]为空，即A[1..j]只包含j-1个元素。同样“A[i+1]<-A[i]”这句代码也会将A[i]置空。
第二重循环不变式为：
（1）A[1...i]有序；
（2）A[i+2,j]有序且所有元素不小于key，同时A[i+2...j]中所有元素不小于A[1...i]中的任意元素；
（3）A[i+1]处是空闲位置。
初始：
i = j-1，A[j]被置空，再加上外重循环的不变式，性质（1）成立，A[i+2..j]包含0个元素所以（2）也成立。（3）明显也成立。
保持：
循环体将值A[i]转移到A[i+1]处，且i减小1。条件（1）显然成立；循环执行之前A[i]>key，A[i]是A[0...i]中最大元素，所以执行之后条件（2）仍成立；条件（3）显然成立。
中止：
当循环中止时，假如i = 0，那么A[1]处为空值，A[2...j]有序（条件2），且A[2...j]所有元素都大于key，那么将key放入A[1]将使A[1...j]有序；如果A[i]<=key，那么由于A[1...i]有序，所以key大于A[1...i]中所有元素，同时由于A[i+2,j]有序且所有元素都大于key，将key放入A[i+1]会使A[1...j]有序。
习题：
2.1-2：
重写过程INSERTION-SORT , 使之按非升序（而不是按非降序）排序。
INSERTION-SORT
for j <- 2 to length[A]
key <- A[j]
Insert A[j]into the sorted sequence A[l...j-1].
i <- j - 1
while i > 0 and A[i] < key
A[i + 1] <- A[i]
i <- i - 1
A[i + 1] <- key2.1-3：
考虑下面的查找问题：
输入：一列数A = ( a1, a2, …， an 〉和一个值v。
输出： 下标i, 使得v = A[i]，或者当v不在A中出现时为NIL 。
写出针对这个问题的线性查找的伪代码，它顺序地扫描整个序列以查找v。利用循环不变式证明算法的正确性。确保所给出的循环不变式满足三个必要的性质。
LinearSearch(A,v)
for i=1 to length[A]
if A[i]=v
return i
return NIL循环不变式证明：
循环不变式：for循环的每次迭代开始前，数组A[1..i-1]中无与v相等的数。
初始化：
在循环的第一次迭代开始前，此时i=1，数组A[1…0]不包含数据，显然v不在A[1…0]中，循环不变式成立。
保持：
在循环某次迭代开始时，假设i=k，不变式是正确的，那么A[1…k-1]不包含值为v的成员，执行此次迭代，假设没有找到与v匹配的成员（若找到就是终止条件），那么执行的结果可知A[k]不等于v，所以A[1...k]不包含值为v的成员，那么在下次迭代开始时，i=k+1，此时A[1...i-1]即A[1...k]，由前面可知不包含值为v的成员，循环不变式成立。
终止：
终止有两种情况，第一种，在某次迭代中，假设i=k，找到了值为v的成员，由“保持”的分析可知，此时A[1...k-1]不包含值为v的成员，循环不变式成立。第二种，没有找到值为v的成员，此时i=n+1，那么A[1...i-1]即为A[1...n]，A[1...n]即为原序列并且不包含值为v的成员，循环不变式成立。
算法分析：
算法分析即指对一个算法所需要的资源进行预测。通常，资源是指我们希望测度的计算时间。
一般来说，算法所需的时间与输入规模同步增长的，因而常常将一个程序的运行时间表示为其输入函数。输入规模的概念与具体问题有关，对许多问题来说，最自然的度量标准是输入元素的个数。
算法的运行时间是指在特定输人时，所执行的基本操作数（或步数）。可以很方便地定义独立于具体机器的“步骤”概念。目前，先采用以下观点，每执行一行伪代码都要花一定量的时间。虽然每一行所花的时间可能不同，但我们假定每次执行第1 行所花的时间都是常量ci，那么在统计出插入排序算法中每行代码的执行次数，就可以给出算法执行时间的一个表达式。
下面我们来分析插入排序算法：
插入排序使用的是算法设计中的增量法：在排序数组A[1...j-1]后，将A[j]插入，形成排好序的数组A[1...j]。
首先给出INSERTION-SORT 过程中，每一条指令的执行时间及执行次数。对j=2, 3, …,n, n=length[A], 设tj为第5 行中while 循环所做的测试次数。当for 或while 循环以通常方式退出（即因为循环头部的测试条件不满足而退出）时，测试要比循环体多执行1次。另外还假定注解部分是不可执行的，因而不占运行时间。
该算法的总体运行时间为每一条语句执行时间之和。如果执行一条语句需要ci 步，又共执行了n 次这条语句，那么它在总运行时间中占ci*n 。求和得：
即使是同样规模下的输入，不同的输入数据也会造成不同的运行时间。
如在插入排序算法中，如果输入数组已有序，就会出现最佳情况：
对j = 2, 3, …， n 中的每一个值，我们发现，若在第5行中，当i取其初始值j-1时，都有A[i]小于等于key。那么对j = 2 , 3, ... , n, 有tj= 1, 最佳运行时间为：
这一运行时间可以表示为an+b , 常量a 和b 依赖于语句的代价Ci，因此，它是n的一个线性函数。
如果输入数组是按照逆序排序的（亦即，是按递降顺序排序的），那么就会出现最坏情况：
我们必须将每个元素A[j] 与整个已排序的子数组A[1. .j-1] 中的每一个元素进行比较，因而，对j=2, 3, …,n, 有tj=j 。
这一最坏情况运行时间可以表示为an2+bn +c , 常量a 、b 和c 仍依赖于语句的代价ci; 因此，这是一个关于n 的二次函数。
在本书的余下部分里，一般考察算法的最坏情况运行时间。一个算法的最坏情况运行时间是在任何输入下运行时间的一个上界。
我们还可以再做进一步的抽象，即运行时间的增长率(rate of growth) , 或称增长的量级(order of growth) 。这样，我们就只考虑公式中的最高次项（例如， an2），因为当n很大时，低阶项相当来说不太重要。另外．还忽略最高次项的常数系数，因为在考虑较大规模输人下的计算效率时，相对于增长率来说，系数是次要的。
如，插入排序的最坏情况时间代价为
习题：
2.2-1：
用
2.2-2：
考虑对数组A中的n个数进行排序的问题：首先找出A中的最小元素，并将其与A[1] 中的元素进行交换。接着，找出A中的次最小元素，并将其与A[2] 中的元素进行交换。对A中头n-1个元素继续这一过程。写出这个算法的伪代码，该算法称为选择排序(selection sort) 。对这个算法来说，循环不变式是什么？为什么它仅需要在头n-1个元素上运行，而不是在所有n个元素上运行？以
SELECTION-SORT{A)
n <- length[A]
for i<-1 to n-1 do
j <-FIND-MIN(A,i,n)
A[j]<->A[i]
end for循环不变式：
在外循环的每次迭代开始前，数组A[1...i-1]保存A中最小的i-1个数，并且是有序的；子数组A[i...n]是A中剩余的未排序元素。
从循环不变式中可知，当循环结束时，即i=n时，A[1...n-1]中是排序好的A中最小的n-1个数，所以剩下的A[n]必然是A中最大的元素，所以不用再比较了。
程序运行时间分析：
最好和最坏情况下时间复杂度均为：
C/C++代码实现如下：
#include <stdio.h>
#include <string.h>
int main() {
int n;
int A[1000];
int k = 0;
while (scanf("%d", &n) != EOF) {
A[k] = n;
k++;
}
for (int i = 0; i < k - 1; i++) {
for (int j = i + 1; j < k; j++) {
if (A[j] < A[i]) {
int temp = A[j];
A[j] = A[i];
A[i] = temp;
}
}
for (int i = 0; i < k; i++)
printf("%d ", A[i]);
printf("\n");
//打印每轮排序后的输出，这样看起来更清晰
}
printf("print the sorted number\n");
for (int i = 0; i < k; i++)
printf("%d ", A[i]);
return 0;
}运行结果如下：
1 7 6 4 2
^D
1 7 6 4 2
1 2 7 6 4
1 2 4 7 6
1 2 4 6 7
print the sorted number
1 2 4 6 7
Process finished with exit code 0Python3代码实现如下：
A = []
while True:
try:
A.append(int(input()))
except:
print('input complete')
break
for i in range(len(A)):
for j in range(len(A)):
if j >= i + 1 and A[j] < A[i]:
A[i], A[j] = A[j], A[i]
for k in range(len(A)):
print(A[k], end=' ')
print('\n', end='')
# 打印每轮排序后的输出，这样看起来更清晰
print('print the sorted number')
for i in range(len(A)):
print(A[i], end=' ')
# python3默认打印会换行，加上end=' '，则每次后面会自动加上' '中内容而不是换行运行结果如下：
8
5
7
4
2
^D
input complete
2 8 7 5 4
2 4 8 7 5
2 4 5 8 7
2 4 5 7 8
2 4 5 7 8
print the sorted number
2 4 5 7 8
Process finished with exit code 0分治法：
有很多算法在结构上是递归的：为了解决一个给定的问题，算法要一次或多次地递归调用其自身来解决相关的子问题。这些算法通常采用分治策略：将原问题划分成n 个规模较小而结构与原问题相似的子问题；递归地解决这些子问题，然后再合并其结果，就得到原问题的解。
分治法在每一层递归上都有三个步骤：
分解： 将原问题分解成一系列子问题；
解决：递归地解各子问题，如果子问题足够小，则直接求解；
合并：将子问题的结果合并成原问题的解。
合并排序：
合并排序应用了分治法，其直观操作如下：
分解：将n个元素分解成各含n/2个元素的子序列
解决：用合并排序法对两个子序列递归地排序
合并：合并两个已排序的子序列以得到排序结果
合并排序的关键步骤在于合并步骤中的合并两个已排序子序列。为做合并，引入一个辅助过程MERGE(A, p, q, r), 其中A是一个数组，p、q和r是下标，满足p小于等于q小于r。该过程假设子数组A[p...q] 和A[q+1...r]都已排好序，并将它们合并成一个已排好序的子数组代替当前子数组A[p.. r] 。
下面来说明该算法的工作过程：
举扑克牌这个例子，假设有两堆牌面朝上地放在桌上，每一堆都是已排序的，最小的牌在最上面。我们希望把这两堆牌合并成一个排好序的输出堆，面朝下地放在桌上。基本步骤包括在面朝上的两堆牌中，选取顶上两张中较小的一张，将其取出后（它所在堆的顶端又会露出一张新的牌）面朝下地放到输出堆中。重复这个步骤，直到某一输入堆为空时为止。这时，把输入堆中余下的牌面朝下地放入输出堆中即可。从计算的角度来看，每一个基本步骤所花时间是个常量，因为我们只是查香并比较顶上的两张牌。又因为至多进行n次比较，所以合并排序的时间为
在伪代码实现时，我们增加一张“哨兵牌”。在每一堆的底部放上一张“哨兵牌" (sentinel card) , 它包含了一个特殊的值，用于简化代码。此处，利用
伪代码：
MERGE(A,p,q,r)
n1 <- q-p+1
n2 <- r-q
create arrays L[1...n1+1] and R[1...n2+1]
for i<-1 to n1
do L[i] <- A[p+i-1]
for j<-1 to n2
do R[j] <- A[q+j]
L[n1+1] <- 极大值哨兵元素
R[n2+1] <- 极大值哨兵元素
i<-1
j<-1
for k<- p to r
do if L[i] <= R[j]
then A[k] <- L[i]
i <- i+1
else A[k] <- R[j]
j <- j+1
MERGE-SORT(A,p,r)
if p<r
then q<-(p+r)/2
MERGE-SORT(A,p,q)
MERGE-SORT(A,q+1,r)
MERGE(A,p,q,r)C/C++代码实现如下：
#include <stdio.h>
#include <string.h>
#include <limits.h>
using namespace std;
void Merge(int *A, int p, int q, int r) {
int n1 = q - p + 1, n2 = r - q;
int *L = new int[n1 + 1];
int *R = new int[n2 + 1];
//分成两部分的子数组分别存在L和R中
for (int i = 0; i < n1; i++)
L[i] = A[p + i];
for (int j = 0; j < n2; j++)
R[j] = A[q + 1 + j];
L[n1] = R[n2] = INT_MAX;
//L和R的哨兵元素
int i = 0, j = 0;
//当L和R均未遍历到哨兵元素时，哪个小哪个就先放到数组A中相应位置
//当其中有一个遍历到哨兵元素时，由于哨兵元素是极大值，故if选择时就会将另一个子数组剩余元素放到数组A中剩余位置中
for (int k = p; k <= r; k++) {
if (L[i] <= R[j]) {
A[k] = L[i];
i = i + 1;
} else {
A[k] = R[j];
j = j + 1;
}
}
}
void MergeSort(int A[], int p, int r) {
if (p < r) {
int q = (p + r) / 2;
//分解，递归地调用MergeSort函数
// 继续分解直到子数组足够小时（即p和q相差1时，此时再调用MergeSort函数已经无法再拆分成更小子问题）开始合并解决子问题
MergeSort(A, p, q);
MergeSort(A, q + 1, r);
//合并子问题的解
Merge(A, p, q, r);
}
}
int main() {
int n;
scanf("%d", &n);
int *A = new int[n];
for (int i = 0; i < n; i++)
scanf("%d", &A[i]);
printf("input complete\n");
MergeSort(A, 0, n - 1);
printf("print the sorted number:\n");
for (int i = 0; i < n; i++)
printf("%d ", A[i]);
return 0;
}运行结果如下：
8
8 7 6 5 4 3 2 1
input complete
print the sorted number
1 2 3 4 5 6 7 8
Process finished with exit code 0Python3代码实现如下：
def merge(a, p, q, r):
L, R = [], []
for k, element in enumerate(a):
if p <= k <= q:
L.append(element)
elif q + 1 <= k <= r:
R.append(element)
# 分成两部分的子数组分别存在L和R中
L.append(float('inf'))
R.append(float('inf'))
# 给L和R两个列表末尾各添加一个无穷大值作为哨兵
i, j = 0, 0
# 当L和R均未遍历到哨兵元素时，哪个小哪个就先放到数组A中相应位置
# 当其中有一个遍历到哨兵元素时，由于哨兵元素时极大值，故if选择时就会将另一个子数组剩余元素放到数组A中剩余位置中
for k, element in enumerate(a, p):
if k <= r:
if L[i] <= R[j]:
a[k] = L[i]
i = i + 1
else:
a[k] = R[j]
j = j + 1
def merge_sort(a, p, r):
if p < r:
q = int((p + r) / 2)
# 分解，递归地调用MergeSort函数
# 继续分解直到子数组足够小时（即p和q相差1时，此时再调用MergeSort函数已经无法再拆分成更小子问题）开始合并解决子问题
merge_sort(a, p, q)
merge_sort(a, q + 1, r)
# 合并子问题的解
merge(a, p, q, r)
A = []
while True:
try:
A.append(int(input()))
except:
print('input complete')
break
merge_sort(A, 0, len(A) - 1)
print("print the sorted number:")
for index, item in enumerate(A):
print(item, end=' ')
# python3默认打印会换行，加上end=' '，则每次后面会自动加上' '中内容而不是换行运行结果如下：
8
7
6
5
4
3
2
1
input complete
print the sorted number:
1 2 3 4 5 6 7 8
Process finished with exit code 0循环不变式：
在第12-17行for循环每一轮迭代的开始，子数组A[p...k-1]包含了L[1...n1+1]和R[1...n2+1] 中的k-p 个最小元素,并且是有序的。此外， L[i]和R[j]是各自所在数组中，未被复制回数组A中的最小元素。
证明该循环不变式：
初始化：
第一轮循环，k=p，i=1，j=1，已排序数组L、R，比较两数组中最小元素L[i]、R[j]，取较小的置于A[p]，此时子数组A[p..p]不仅是已排序的（仅有一个元素），而且是所有待排序元素中最小的。若最小元素是L[i]，取i=i+1，即i指向L中未排入A的所有元素中最小的一个；同理，j之于R数组也是如此。
保持：
若A[p..k]是已排序的，由计算方法知，L中i所指、R中j所指及其后任意元素均大于等于A[p..k]中最大元素A[k],当k=k+1，A[k+1]中存入的是L[i]、R[j]中较小的一个，但是仍有A[k] <= A[k+1]，而此时，子数组A[p..k+1]也必是有序的，i、j仍是分别指向L、R中未排入A的所有元素中最小的一个。
终止：
k=r+1时终止跳出循环，此时，A[p..r]是已排序的，且此即原待排序子数组，故算法正确。
当一个算法中含有对其自身的递归调用时，其运行时间可以用一个递归方程（或递归式）来表示。
合并算法的递归式：
n<=c时,T(n)=Θ(1)；否则T(n)=aT(n/b)+D(n)+C(n)
D(n)是分解该问题所用时间，C(n)是合并解的时间；对于合并排序算法，a和b都是2
T(n)在最坏的情况下合并排序n个数的运行时间分析：
当n>1时，将运行时间如下分解：
分解：这一步仅仅算出子数组的中间位置，需要常量时间，因而D(n)=
解决：递归地解为两个规模为n/2的子问题，时间为T(n/2)
合并：含有n个元素的子数组上，MERGE过程的运行时间为C(n) =
故n=1时,T(n)=
将上式改写为：
n=1时,T(n)=c；n>1时T(n)=2T(n/2)+ cn
第4 章将介绍“主定理"(master theorem) , 它可以用来证明T(n)为
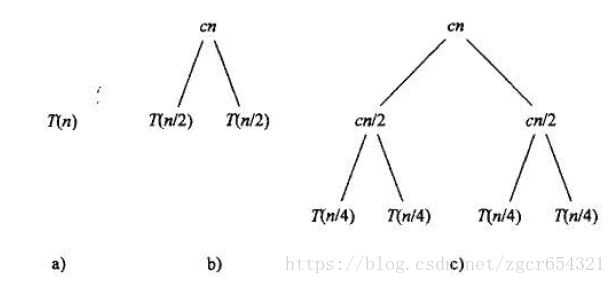
将这个算法构造递归树：
其构造的递归树中，顶层总代价为cn（n个点的集合）。往下每层总代价不变，第i层的任一节点代价为c(n/2^i)（共2^i个节点总代价仍然是cn）。最底层有n个节点（n*1），每个点代价为c。此树共有lgn+1层。
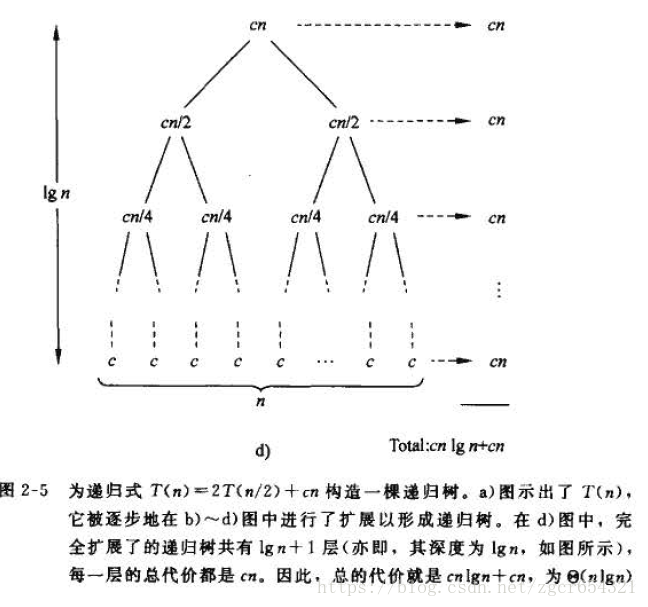
要计算递归式
在该树中，总共有lgn+1层，每一层的代价都是cn, 于是，整棵树的总代价就是cn(lgn+1) = cnlgn+cn。忽略低阶项和常量c, 即得到结果
习题：
2.3-3：
利用数学归纳法证明：当n是2的整次幂时，递归式
的解为
2.3-4：
插入排序可以如下改写成一个递归过程：为排序A[1...n]，先递归地排序A[1...n-1]，然后再将A[n]插入到已排序的数组中去。对于插入排序的这一递归版本，为他的运行时间写一个递归式。
