Preface
可并堆,一个听起来很NB的数据结构,实际上比一般的堆就多了一个合并的操作。
考虑一般的堆合并时,当我们合并时只能暴力把一个堆里的元素一个一个插入另一个堆里,这样复杂度将达到\(\log(|A|)+\log(|B|)\),极限数据下显然是要T爆的。
所以我们考虑使用一种性价比最高的可并堆——左偏树,它的思想以及代码都挺简单而且效率也不错。
学习和参考自这里
What is Leftist Tree
左偏树,顾名思义就是像左偏的树,但是这样抽象的表述肯定是不符合我们学OI的人的背板子严谨的态度的。
我们给出一些定义:
- 外节点:当且仅当这个节点的左子树和右子树中的一个是空节点,注意外节点不是叶子节点
- 距离(或者是高度?):对于左偏树中的一个节点\(x\),到它的子节点中,离它最近的一个外结点经过的边数称为它的距离,记为\(dist_x\)。特别地,外结点的距离为0,空节点(null)的距离为\(-1\)。
然后跟着这个定义我们可以得出一些性质:
- 堆性质:对于左偏树中的一个非叶节点应满足堆的性质。如果是大根堆,应满足任意非叶节点的值大于左右孩子(如果有的话)的值。即\(val_x\ge val_{lson(x)},val_{rson(x)}\)
- 左偏性质:对于左偏树中的任意节点满足它的左子树(如果有的话)的距离大于等于右子树(如果有的话)的距离。即\(dist_{lson(x)}\ge dist_{rson(x)}\)
- 传递性?:左偏树任意节点的左右儿子(如果有的话)都是一棵左偏树
废话
由这几条性质可以发现左偏树是具有左偏性质的堆有序二叉树。
同时还有一条不可忽视的终于引理:左偏树中的节点的距离总是满足\(dist_x=dist_{rsom(x)}+1\)
证明:同时由距离的定义以及左偏性质即可得出。
The operator of Leftist Tree
BB了这么就性质啥的抽象东西,是时候讲点真正有用的东西了。
Merge
可并堆的基本操作(也是必备操作)自然是快速地完成合并了,同时合并也是左偏树的灵魂部分,只要说掌握了合并的话就可以直接拿着左偏树大力切题了。
以下假定大根堆的情况,我们假定要合并的两个左偏树(注意单个节点也是左偏树)的根为\(x,y\)
我们首先维护堆的性质,令\(val_x>val_y\),即当值不满足的时候\(\operatorname{swap}(x,y)\)
那么我们发现这时候就要把\(y\)插入\(x\)的子树中了,换句话说,就是要把\(y\)和\(x\)的子树合并。
那么和谁合并呢?考虑我们辛辛苦苦维护的左偏性质,由于右边的链长小于等于左边的,所以为了保证复杂度肯定是直接和\(dist\)小的合并了,于是我们合并\(rson(x)\)和\(y\)
但是插入后右子树的\(dist\)可能会大于左边了这样就变右偏树了,我们肯定是不允许的,于是我们判断一下这种情况,如果有就直接交换左右子树(注意直接交换编号即可)即可。
那么什么时候结束呢,当然是当\(x\)或\(y\)中一者为空了啦。所以我们可以比较轻松的得到合并的代码(返回合并的堆的堆顶编号):
inline int merge(int x,int y)
{
if (!x||!y) return x+y; if (c[x]<c[y]) swap(x,y);
rc(x)=merge(rc(x),y); if (node[lc(x)].dis<node[rc(x)].dis) swap(lc(x),rc(x));
node[x].dis=node[rc(x)].dis+1; return x;
}这里放一张Luogu上找到的动图可以更加生动地理解下:
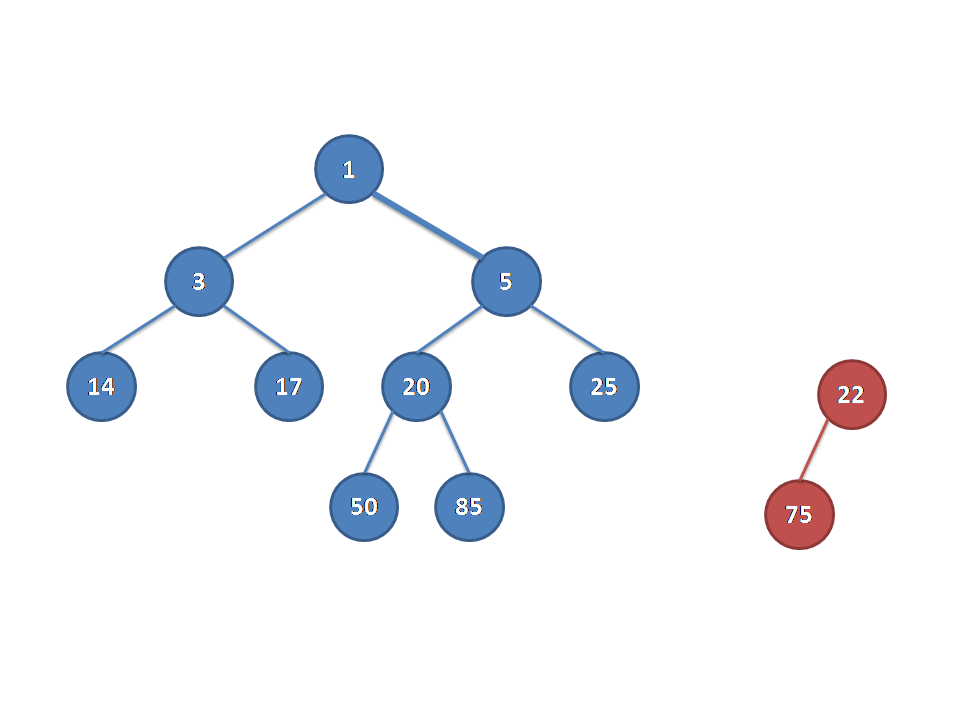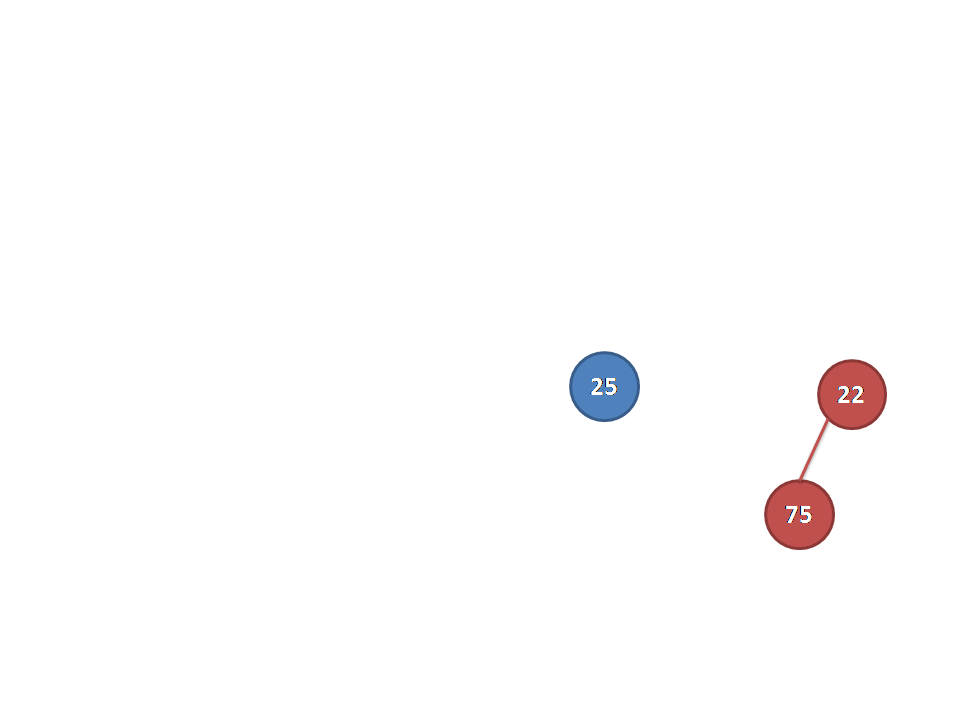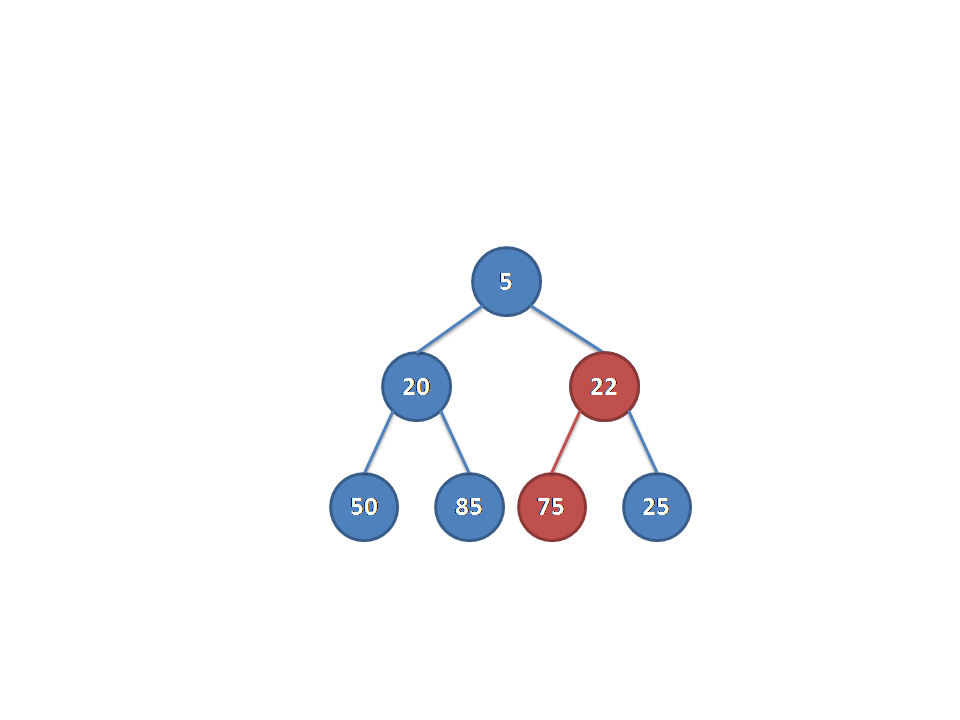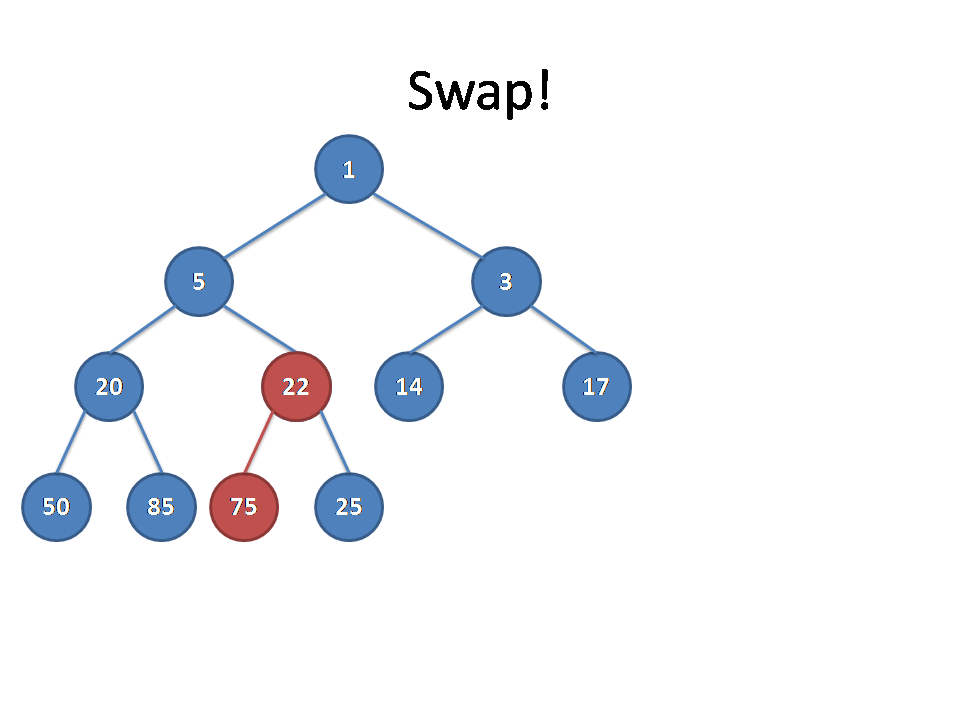
复杂度的话类似启发式的思想发现是\(O(\log)\)级别的。
push
push的本质就是把一个只有一个节点的左偏树于一颗左偏树合并,因此直接用merge即可。
top
这个直接返回根节点的权值即可。
pop
删除根节点的话可以考虑合并根节点的两个子树,代码
inline void remove(int &x)
{
x=merge(lc(x),rc(x));
}板子题:Luogu P3377 【模板】左偏树(可并堆)
这个我们维护小根对的时候再维护一个父节点的信息即可查询两个数是否在同一颗左偏树里了。
CODE
#include<cstdio>
#include<cctype>
using namespace std;
const int N=100005;
struct Leftist_Tree
{
int ch[2],val,dis,fa;
}node[N];
int n,m,x,y,opt;
inline char tc(void)
{
static char fl[100000],*A=fl,*B=fl;
return A==B&&(B=(A=fl)+fread(fl,1,100000,stdin),A==B)?EOF:*A++;
}
inline void read(int &x)
{
x=0; char ch; while (!isdigit(ch=tc()));
while (x=(x<<3)+(x<<1)+ch-'0',isdigit(ch=tc()));
}
inline void write(int x)
{
if (x>9) write(x/10);
putchar(x%10+'0');
}
inline void swap(int &a,int &b)
{
int t=a; a=b; b=t;
}
inline int merge(int x,int y)
{
if (!x||!y) return x+y;
if (node[x].val>node[y].val||(node[x].val==node[y].val&&x>y)) swap(x,y);
node[x].ch[1]=merge(node[x].ch[1],y); node[node[x].ch[1]].fa=x;
if (node[node[x].ch[0]].dis<node[node[x].ch[1]].dis) swap(node[x].ch[0],node[x].ch[1]);
node[x].dis=node[node[x].ch[1]].dis+1; return x;
}
inline void remove(int x)
{
node[x].val=-1; node[node[x].ch[0]].fa=node[node[x].ch[1]].fa=0;
merge(node[x].ch[0],node[x].ch[1]);
}
inline int getfather(int x)
{
while (node[x].fa) x=node[x].fa; return x;
}
int main()
{
//freopen("CODE.in","r",stdin); freopen("CODE.out","w",stdout);
register int i; read(n); read(m); node[0].dis=-1;
for (i=1;i<=n;++i) read(node[i].val);
while (m--)
{
read(opt); read(x); if (opt^2)
{
read(y); int fx=getfather(x),fy=getfather(y);
if (~node[fx].val&&~node[fy].val&&fx!=fy) merge(fx,fy);
} else
{
int fx=getfather(x); if (!(~node[fx].val)) puts("-1"); else
write(node[fx].val),putchar('\n'),remove(fx);
}
}
return 0;
}例题
- Luogu P1552 [APIO2012]派遣可并堆好题。考虑以每个点为领导者计算答案那么可选的点都在这颗子树中,那么考虑用的人最多我们就贪心的把大的扔掉,回溯时合并两个堆即可。左偏树处理。
- BZOJ 1367: [Baltic2004]sequence 可并堆好题,一眼看不出。考虑先求不降序列的情况,发现可以对原序列的所有不升序列进行分割,这样必然是取中位数(反证法)。然后用左偏树统计中位数并支持合并即可。
Postscript
可并堆算是介于TG和省选直接的尴尬内容的吧,往年NOIp的话不见出现过。
左偏树虽说在效率上次于配对堆,斐波那契堆这些神仙数据结构,但是它简单的思想以及码量都是很良心的。
还是稍微要掌握一下的吧。