第五章 图-习题

1.下列关于无向连通图特性的叙述中，正确的是？

Ⅰ．所有顶点的度之和为偶数

Ⅱ．边数大于顶点个数

Ⅲ．至少有一个顶点的度为1

• 只有Ⅰ

• 只有Ⅱ

• Ⅰ和Ⅱ

• Ⅰ和Ⅲ

解析：A
1，每条边连接两个顶点，所有顶点的度之和等于边数的2倍，是偶数，正确
2，如两个顶点一条边的图就不满足这个条件，错
3，如三个顶点三条边连成一个三角形的图每个顶点度为2，错 

2.若无向图 G 中含 7 个顶点，则保证图 G 在任何情况下都是连通的，则需要的边数

最少是（         ）

• 6

• 15

• 16

• 21

解析： 在任何情况下，意思就是说，只要有给定的边数则必定会连通，无论你的边怎么安排，怎么放，图G都能构成连通。

因为，只需要n-1个顶点构成完全无向图，再加上1条边和剩下的顶点相连，就能让n个顶点连通。

由题，n是7，因此6个顶点需要构成完成无向图需要5+4+3+2+1=6*5/2=15，再加1是16条边。

因此，只要有16条边，图G一定会连通，不管你边怎么放。

因此选C。

至于A选项的6条边，是图 G 是连通的最少边数，不是在任何情况下的。

3.对下图进行拓 扑 排序，可以得到不同的拓 扑 序列的个数是（B）

• 4

• 3

• 2

• 1

• 解析：

拓扑排序的步骤：由AOV网构造拓扑序列的拓扑排序算法主要是循环执行以下两步，直到不存在入度为0的顶点为止。

(1) 选择一个入度为0的顶点并输出之；

(2) 从网中删除此顶点及所有出边。

循环结束后，若输出的顶点数小于网中的顶点数，则输出“有回路”信息，否则输出的顶点序列就是一种拓扑序列

4.下列关于图的叙述中，正确的是 。

Ⅰ ．回路是简单路径

Ⅱ ．存储稀疏图，用邻接矩阵比邻接表更省空间

Ⅲ ．若有向图中存在拓扑序列，则该图不存在回路

• 仅Ⅱ

• 仅Ⅰ、Ⅱ

• 仅Ⅲ

• 仅Ⅰ、Ⅲ

 解析：

如果路径上的各顶点均不互相重复，称这样的路径为简单路径。如果路径上的第一个顶点与最后一个顶点重合，这样的路径称为回路(cycle)或环或圈。如在图1中，回路有

等等 [1]  。

第一个顶点和最后一个顶点相同的路径称为回路；序列中顶点不重复出现的路径称为简单路径；回路显然不是简单路径，故 Ⅰ 错误；稀疏图是边比较少的情况，此时用邻接矩阵的空间复杂度为 O(n2) ，必将浪费大量的空间，而邻接表的空间复杂度为 O(n+e) ，应该选用邻接表，故 Ⅱ 错误。存在回路的有向图不存在拓扑序列，若拓扑排序输出结束后所余下的顶点都有前驱，则说明只得到了部分顶点的拓扑有序序列，图中存在回路，故 Ⅲ 正确。 

5.对有n 个顶点、 e 条边且使用邻接表存储的有向图进行广度优先遍历，其算法的时间复杂度是（ ）。 

• O(n)

• O(e)

• O(n+e)

• O(n×e)

解析：

对于DFS,BFS遍历来说，时间复杂度和存储结构有关：

1.若采用邻接矩阵存储，时间复杂度为O(n^2);    注意不是n*e

2.若采用邻接链表存储，时间复杂度为O(n+e);

 6.若用邻接矩阵存储有向图，矩阵中主对角线以下的元素均为零，则关于该图拓扑序列的结论是（）。

• 存在，且唯一

• 存在，且不唯一

• 存在，可能不唯一

• 无法确定是否存在

解析:

上三角矩阵说明有向图只有序号小的节点单向指向序号大的节点，所以存在拓扑序列。加上条件A[i][i+1]全为1才是唯一的，题目没有说明这一点，所以是可能唯一      (很经典，唯一性)

7.如图所示的有向带权图，若采用迪杰斯特拉（Dijkstra）算法求从源点a到其他各顶点的最短路径，则得到的第一条最短路径的目标顶点是b，第二条最短路径的目标顶点是c，后续得到的其余各最短路径的目标顶点依次是（）。

• d,e,f

• e,d,f

• f,d,e

• f,e,d

解析：从a到各顶点的最短路径的求解过程：

顶点	第1趟	第2趟	第3趟	第4趟	对5趟
b	(a,b) 2
c	(a,c) 5	(a,b,c) 3
d	∞	(a,b,d) 5	(a,b,d) 5	(a,b,d) 5
e	∞	∞	(a,b,c,f) 4
f	∞	∞	(a,b,c,e) 7	(a,b,c,e) 7	(a,b,d,e) 6
集合S	{a,b}	{a,b,c}	{a,b,c,f}	{a,b,c,f,d}	{a,b,c,f,d,e}

后续目标顶点依次为f,d,e，

【排除法】对于A，若下一个顶点为d，路径a,b,d的长度5，而a,b,c,f的长度仅为4，显然错误。同理可以排除B。将f加入集合S后，采用上述的方法也可以排除D。

8.下列关于最小生成树的叙述中，正确的是（）。

Ⅰ．最小生成树的代价唯一

Ⅱ．所有权值最小的边一定会出现在所有的最小生成树中

Ⅲ．使用普里姆（Prim）算法从不同顶点开始得到的最小生成树一定相同

Ⅳ．使用普里姆算法和克鲁斯卡尔（Kruskal）算法得到的最小生成树总不相同

• 仅Ⅰ

• 仅Ⅱ

• 仅Ⅰ、Ⅲ

• 仅Ⅱ、Ⅳ

解析：
对于I，最小生成树的树形可能不唯一（这是因为可能存在权值相同的边），但是代价一定是唯一的，I正确。对于II，如果权值最小的边有多条并且构成环状，则总有权值最小的边将不出现在某棵最小生成树中，II错误。对于III，设N个结点构成环，N-1条边权值相等，则从不同的顶点开始普里姆算法会得到N- 1中不同的最小生成树，III错误。对于IV，当最小生成树唯一时（各边的权值不同），普里姆算法和克鲁斯卡尔算法得到的最小生成树相同，IV错误。 

9.设图的邻接矩阵A 如下所示。各顶点的度依次是（ ）。

• 1， 2， 1， 2

• 2， 2， 1， 1

• 3， 4， 2， 3

• 4， 4， 2， 2

解析：

     无向图的边数组（邻接矩阵）是对阵矩阵。各顶点的度为邻接矩阵中对应行的元素之和。

     有向图的各顶点的度为出度加上入度之和。出度为对应顶点所在行的所有元素之和，入度为对应顶点所在列的所有元素之和。

     该图明显为有向图。所以各个顶点的度为其出度和入度之和，即所在行和列元素之和。

10.若对如下无向图进行遍历，则下列选项中，不是广度优先遍历序列的是（）。D

• h， c， a， b， d， e， g， f

• e， a， f， g， b， h， c， d

• d， b， c， a， h， e， f， g

• a， b， c， d， h， e， f， g

解析：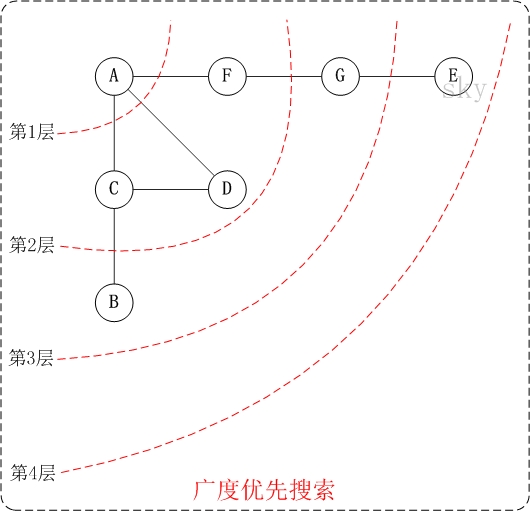 

第1步：访问A。 
第2步：依次访问C,D,F。 
    在访问了A之后，接下来访问A的邻接点。前面已经说过，在本文实现中，顶点ABCDEFG按照顺序存储的，C在"D和F"的前面，因此，先访问C。再访问完C之后，再依次访问D,F。 
第3步：依次访问B,G。 
    在第2步访问完C,D,F之后，再依次访问它们的邻接点。首先访问C的邻接点B，再访问F的邻接点G。 
第4步：访问E。 
    在第3步访问完B,G之后，再依次访问它们的邻接点。只有G有邻接点E，因此访问G的邻接点E。

因此访问顺序是：A -> C -> D -> F -> B -> G -> E

这题，a开始的话，接下来明显是bhe，顺序不分先后 

11.下列AOE 网表示一项包含 8 个活动的工程。通过同时加快若干活动的进度可以缩短整个工程的工期。下列选项中，加快其进度就可以缩短工程工期的是（ ）。

• c 和 e

• d 和 e

• f 和 d

• f 和 h

关键路径详解： 

解析：

这个网有三条关键路径：

• b、d、c、g
• b、d、e、h
• b、f、h

缩短工期的活动要涵盖三条路径。

12.对如下所示的有向图进行拓扑排序，得到的拓扑序列可能是 （D）

• 3,1,2,4,5,6

• 3,1,2,4,6,5

• 3,1,4,2,5,6

• 3,1,4,2,6,5

解析：

每次选取极大顶点（入度为0的顶点），并把它跟它的出度一起从图中删掉
第一次删掉3
第二次删掉1
第三次删掉4
第四次可以删掉2或者6，若依据选项CD删掉2，那么第五次删掉6，最后删掉5
314265，选D

13.设有向图G=(V,E)，顶点集V={V0,V1,V2,V3}，边集E={<v0,v1>，<v0,v2>，<v0,v3>，<v1,v3>}。若从顶点V0 开始对图进行深度优先遍历，则可能得到的不同遍历序列个数是 。

• 2

• 3

• 4

• 5

解析：

画出该有向图图形如下：

采用图的深度优先遍历，共5种可能：<v0, v1, v3, v2>，<v0, v2, v3, v1>，<v0, v2, v1, v3>，<v0, v3, v2, v1>，<v0, v3, v1, v2>，选D。

14.求下面带权图的最小（代价）生成树时，可能是克鲁斯卡（Kruskal）算法第2次选中但不是普里姆（Prim）算法（从V4开始）第2次选中的边是 。  C

• (V1,V3)

• (V1,V4)

• (V2,V3)

• (V3,V4)

解析：

Kruskal算法是按权值选边，若选边后不形成回路,则保留作为一条边,若形成回路则除去

Prim算法是每次从当前的二叉树节点向外延伸的，选择权值最小的边

克鲁斯卡（Kruskal）算法   和    普里姆（Prim）算法（从 V4 开始）第1次选中的边都是(v4,v1) 。Kruskal算法第二次可以选择(v1,v3),   (v2,v3),   (v3,v4);   Prim算法第二次可以选择(v1,v3),   (v3,v4)

15.下列选项中，不是下图深度优先搜索序列的是 。D

• V1, V5, V4, V3, V2

• V1, V3, V2, V5, V4

• V1, V2, V5, V4, V3

• V1, V2, V3, V4, V5

解析：按深度优先搜索就行，2不可以直接到3 

16.若将n个顶点e条弧的有向图采用邻接表存储，则拓扑排序算法的时间复杂度是 。

• O(n)

• O(n+e)

• O(n2)

• O(n*e)

解析：

根据拓扑排序的规则，输出每个顶点的同时还要删除以它为起点的边，这样对各顶点和边都要进行遍历，故拓扑排序的时间复杂度为O(n+e)

17.链接：使用迪杰斯特拉（Dijkstra）算法求下图中从顶点1到其他各顶点的最短路径，依次得到的各最短路径的目标顶点是 。B

• 5, 2, 3, 4, 6

• 5, 2, 3, 6, 4

• 5, 2, 4, 3, 6

• 5, 2, 6, 3, 4

解析：

根据Dijkstra算法，从顶点1到其余各顶点的最短路径如下表所示：

18.：带权图（权值非负，表示边连接的两顶点间的距离）的最短路径问题是找出从初始顶点到目标顶点之间的一条最短路径。假设从初始顶点到目标顶点之间存在路径，现有一种解决该问题的方法：

① 设最短路径初始时仅包含初始顶点，令当前顶点u为初始顶点；

② 选择离u最近且尚未在最短路径中的一个顶点v，加入到最短路径中，修改当前顶点u=v；

③ 重复步骤②，直到u是目标顶点时为止。

请问上述方法能否求得最短路径？若该方法可行，请证明之；否则，请举例说明。

解析：该方法不一定能（或不能）求得最短路径。（4分）

举例说明：（6分）

图A-4中，设初始顶点为1，目标顶点为4，欲求从顶点1到顶点4之间的最短路径，显然这两点之间的最短路径长度为2。利用给定方法求得的路径长度为3，但这条路径并不是这两点之间的最短路径。

图A-5中，设初始顶点为1，目标顶点为3，欲求从顶点1到顶点3之间的最短路径。利用给定的方法，无法求出顶点1到顶点3的路径。

图A-4	图A-5

利用给定的方法，无法求出顶点1到顶点3的路径。

【评分说明】①若考生回答“能求得最短路径”，无论给出何种证明，均不给分。

② 考生只要举出类似上述的一个反例说明“不能求得最短路径”或答案中体现了“局部最优不等于全局最优”的思想，均可给6分；若举例说明不完全正确，可酌情给分。

题外话：最小生成树与最短路径的区别

最小生成树能够保证整个拓扑图的所有路径之和最小，但不能保证任意两点之间是最短路径。一般用 Kruskal 和 Prim算法
最短路径是从一点出发，到达目的地的路径最小   一般用 Dijkstra算法

19.已知有6个顶点（顶点编号为0～5）的有向带权图G，其邻接矩阵A为上三角矩阵，按行为主序（行优先）保存在如下的一维数组中。

4

6

∞

∞

∞

5

∞

∞

∞

4

3

∞

∞

3

3

要求：

（1）写出图G的邻接矩阵A。

（2）画出有向带权图G。

（3）求图G的关键路径，并计算该关键路径的长度。

解析：（注意对角就是自己到自己，所以对角全0，就很好求了）
1）在上三角矩阵A[6][6]中，第1行至第5行主对角线上方的元素个数分别为5、4、3、2、1，由此可以画出压缩存储数组中的元素所属行的情况，如下图所示。

用“平移”的思想，将前5个、后4个、后3个、后2个、后1个元素，分别移动到矩阵对角线（“0”）右边的行上。图G的邻接矩阵A如下所示。

2）根据上面的邻接矩阵，画出有向带权图G，如下图所示。

 3）按照算法，先计算各个事件的最早发生时间，各个事件的最迟发生时间

    事件最早发生时间 （左到右取最大值）通过前驱加边

    事件最迟发生时间 （右到左取最小值）通过后驱减边

i	0	1	2	3	4	5
ve(i)	0	4	9	13	12	16
vl(i)	0	4	9	13	13	16

 接下来计算所有活动的最早和最迟发生时间

   活动的最早：取前驱事件最早

   活动的最迟：取后驱事件最晚减边

	a0→1	a0→2	a1→2	a2→3	a2→4	a3→5	a4→5
e()	0	0	4	9	9	13	12
l()	0	3	4	9	10	13	13
l-e	0	3	0	0	1	0	1

满足l()-e()=0的路径就是关键路径，所以关键路径为a0→1、a1→2、a2→3、a3→5，如下图所示（粗线表示），长度为4+5+4+3=16。

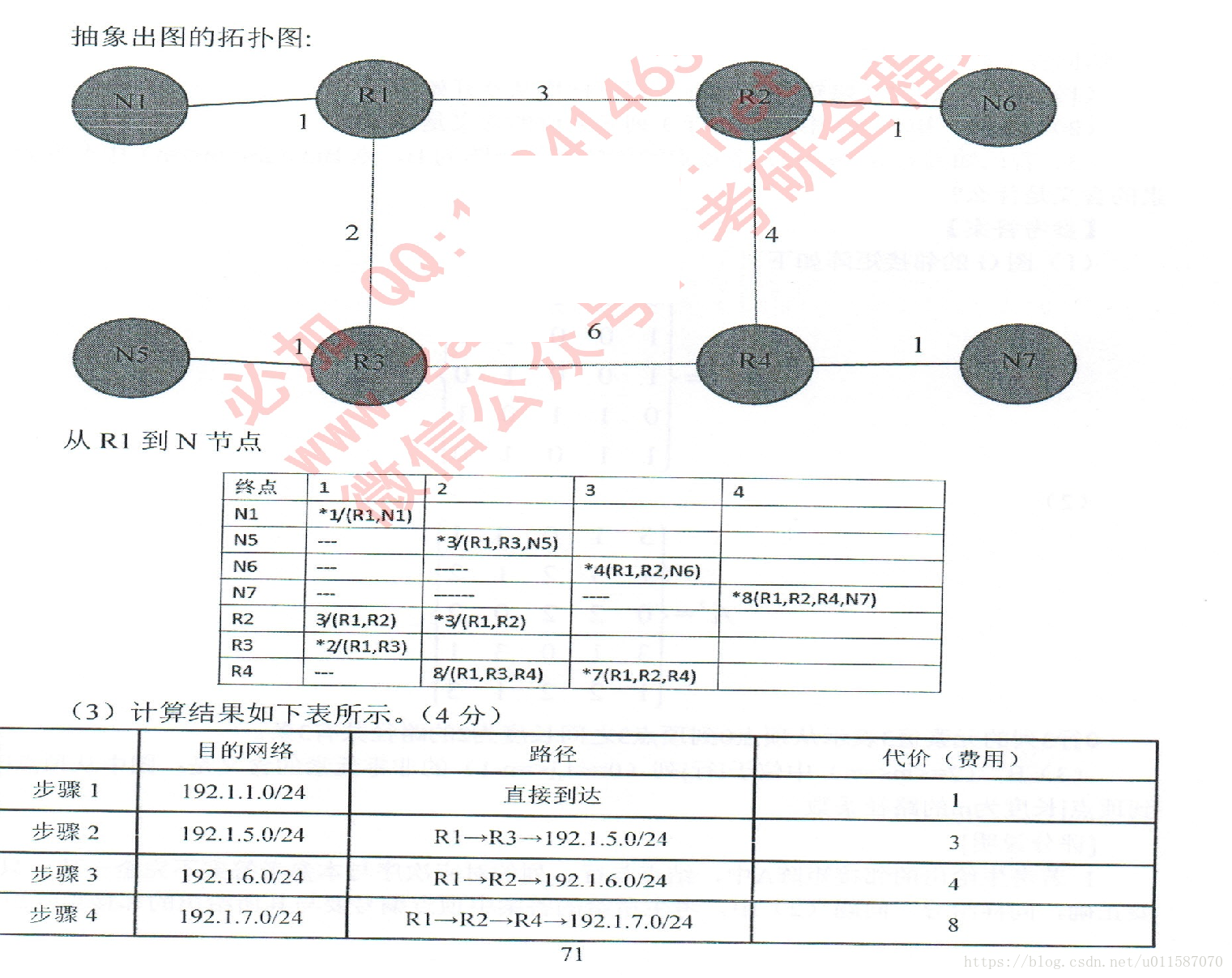
20.：某网络中的路由器运行OSPF路由协议，题42表是路由器R1维护的主要链路状态信息（LSI），题42图是根据题42表及R1的接口名构造出来的网络拓扑。

题42表R1所维护的LSI

		R1的LSI	R2的LSI	R3的LSI	R4的LSI	备注
Router ID		10.1.1.1	10.1.1.2	10.1.1.5	10.1.1.6	标识路由器的IP地址
Link1	ID	10.1.1.2	10.1.1.1	10.1.1.6	10.1.1.5	所连路由器的RounterID
	IP	10.1.1.1	10.1.1.2	10.1.1.5	10.1.1.6	Link1的基本IP地址
	Metric	3	3	6	6	Link1的费用
Link2	ID	10.1.1.5	10.1.1.6	10.1.1.1	10.1.1.12	所连路由器的RounterID
	IP	10.1.1.9	10.1.1.13	10.1.1.10	10.1.1.14	Link2基本IP地址
	Metic	2	4	2	4	Link2费用
Net1	Prefix	192.1.1.0/24	192.1.6.0/24	192.1.7.0/24	192.1.7.0/24	直接网络Net1的网络前缀
	Metric	1	1	1	1	到达直连网络Net1的费用

题42图  R1构造的网络拓扑

请回答下列问题。

（1） 本题中的网络可抽象为数据结构中的哪种逻辑结构？

（2） 针对题42表中的内容，设计合理的链式存储结构，以保存题42表中的链路状态信息（LSI）。要求给出链式存储结构的数据类型定义，并画出对应题42表的链式存储结构示意图（示意图中可仅以ID标识节点）。

（3） 按照迪杰斯特拉（Dijikstra）算法的策略，依次给出R1到达题42图中子网192.1.x.x的最短路径及费用。

 解析：

（1） 本题中的网络可抽象为图结构。 
（2） 链式存储结构的数据类型定义如下： 

typedef struct LinkNode
{
    unsigned int ID; //所连路由器的 Router ID
    unsigned int IP; //本地 IP 地址
}LinkNode; //Link 的结构
typedef struct NetNode
{
    unsighed int Prefix; //IP 前段
    unsighed int Mask; //掩码
}NetNode; //Net 的结构
typedef struct ArcNode
{
    int Flag; //当 Flag=1 时， 表示 Link； 当 Flag=2 时，表示 Net
    union
    {
        LinkNode Lnode;
        NetNode Nnode;
    }LinkORNet; //用 union 定义 Link 结点和 Net 结点
    unsighed int Metric; //费用
    struct ArcNode * Next; //用于指向下一个弧结点的指针
}ArcNode; //弧结点的结构
typedef struct HNode
{
    unsighed int RouterID; //路由器的 Router ID
    ArcNode * LN_link; //用于指向弧结点的指针
    struct HNode * Next; //用于指向下一个表头结点的指针
}HNode; //表头结点的结构

对应题42 表的链式存储结构示意图如下。

21.已知含有5个顶点的图G如下图所示。

请回答下列问题：

1）写出图G的邻接矩阵A（行、列下标从0开始）。

2）求A2，矩阵A2中位于0行3列元素值的含义是什么？

3）若已知具有n（n≥2）个顶点的图的邻接矩阵为B，则Bm（2≤m≤n）中非零元素的含义是什么？

解析：

1）图G的邻接矩阵A如下：

2）A2如下：

0行3列的元素值3表示从顶点0到顶点3之间长度为2（2次方所以长度为2）的路径共有3（0行3列处为3.这条不确定，找不到这个定理出处）条。

3）Bm（2≤m≤n）中位于i行j列（0≤i，j≤n-1）的非零元素的含义是：图中从顶点i到顶点j长度为m的路径条数。（这条好像也是定理把，在书上找不到这条？）

22.如果一棵非空k（k≥2）叉树T中每个非叶结点都有k个孩子，则称T为正则k叉树。请回答下列问题并给出推导过程。

（1）若T有m个非叶结点，则T中的叶结点有多少个？

（2）若T的高度为h（单结点的树h=1），则T的结点数最多为多少个？最少为多少个？

解答：

（1）根据定义，正则k叉树中仅含有两类结点；叶结点（个数记为n0）和度为k的分支结点（个数记为n1）。树T中的结点总数n=n0+nk=n0+m。树中所含的边数e=n-1，这些边均为m个度为k的结点发出的，即e=m×k。整理得：n0+m=m×k+1，故n0=（k-1）×m+1。（3分）

（2）高度为h的正则k叉树T中，含最多结点的树形为：除第h层外，第1到第h-1层的结点都是度为k的分支结点；而第h层均为叶结点，即树是“满”树。此时第j（1≤j≤h）层结点数为，结点总数M1为：

（3分）

含最少结点的正则k叉树的树形为：第1层只有根结点，第2到第h-1层仅含1个分支结点和k-1个叶结点，第h层有k个叶结点。即除根外第2到第h层中每层的结点数均为k，故T中所含结点总数M2为：

M2=1+(h-1)×k （2分）

【评分说明】

①参考答案仅给出一种推导过程，若考生采用其他推导方法且正确，同样给分。②若考生仅给出结果，但没有推导过程，则（1）、（2）的最高得分分别是2分和3分。若推导过程或答案不完全正确，酌情给分。