比较好想的一道题，直接用队列滑窗，因为扫一遍往队列里加东西时，改变的只有一个值，开桶储存好就行了！
#include<bits/stdc++.h> using namespace std; int n, k, r; inline int min(int a, int b) { return a > b ? b : a; } inline int max(int a, int b) { return a > b ? a : b; } int sum[200005], q[200005], cnt[200005], vis[200005], ned[200005]; int a[200005]; int main() { freopen("drop.in", "r", stdin); freopen("drop.out", "w", stdout); int T; scanf("%d", &T); while(T --) { memset(sum, 0, sizeof(sum)); memset(q, 0, sizeof(q)); memset(cnt, 0, sizeof(cnt)); memset(vis, 0, sizeof(vis)); memset(ned, 0, sizeof(ned)); scanf("%d%d%d", &n, &k, &r); int tot = 0, fl = 0; for(int i = 1; i <= n; i ++) { scanf("%d", &a[i]); sum[a[i]] ++; } for(int i = 1; i <= r; i ++) { int b, p; scanf("%d%d", &b, &p); if(!vis[b]) vis[b] = 1, tot ++; if(sum[b] < p) { fl = 1; break; } ned[b] = max(ned[b], p); } if(fl) { printf("DESTROY ALL\n"); continue; } int ans = 0x3f3f3f3f; int h = 0, t = 0, now = 0; for(int i = 1; i <= n; i ++) { if(vis[a[i]]) { q[++t] = i; cnt[a[i]] ++; if(cnt[a[i]] == ned[a[i]]) now ++; } while(now == tot && h < t) { ans = min(ans, q[t] - q[h+1] + 1); cnt[a[q[h+1]]] --; if(cnt[a[q[h+1]]] < ned[a[q[h+1]]]) now --; h ++; } } printf("%d\n", ans); } return 0; }
考场上想到$2-sat$但是忘得差不多了，打死都理不清楚关系。
这道题算是$2-sat$板子题了，主要是如何判断的思想。
首先题目条件疯狂暗示，但是和$2-sat$的一般理解方式不同。题目上给的约束条件我们按$2-sat$让他们避免相连，实际上就是题目中的防守文明，我们要摧毁文明，实际上是要让防守文明失效。即至少有一个点和它的负点相互相通。因为$n$很小就可以用两次$dfs$实现，然后就是分类讨论来判断该加几条边。
1、假如初始连边中就有某一个点对正负点相互连接，答案就是0.
2、假如一个点对中正点连向负点：
1）
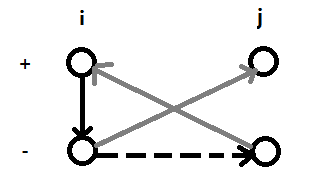如果负点可以连向另一点对的正点，根据$2-sat$的对称行，另一点对的负点一定可以连向当前点对的正点，所以我们只用加条件$(i,j)$，就是在$-i$和$-j$之间连了一条边，使i点对相互连通。
2）如果负点没有连向任意点对的正点，那么一定无解，输出$No Way$。
3、假如一个点对中负点连向正点：
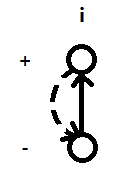那么只用加一个条件$(i,i)$，相当于在$i$和$-i$间连边即可。
4、假如点对之间没有连边：
1）
将2、3结合，但是必须满足2的条件，这样加两条边即可。
2）没有2的条件，就无法加边，输出$No Way$。
#include<bits/stdc++.h> using namespace std; struct Node { int u, v, nex; Node(int u = 0, int v = 0, int nex = 0) : u(u), v(v), nex(nex) { } } Edge[4005]; int h[4004], stot; void add(int u, int v) { Edge[++stot] = Node(u, v, h[u]); h[u] = stot; } int vis[4005]; void dfs(int u) { vis[u] = 1; for(int i = h[u]; i; i = Edge[i].nex) { int v = Edge[i].v; if(vis[v]) continue; dfs(v); } } int n, m; int main() { freopen("god.in", "r", stdin); freopen("god.out", "w", stdout); int T; scanf("%d", &T); while(T --) { memset(h, 0, sizeof(h)); stot = 0; scanf("%d%d", &n, &m); for(int i = 1; i <= m ; i++) { int x, y; scanf("%d%d", &x, &y); if(x > 0 || y < 0) swap(x, y); if(x > 0 && y > 0) { add(x, y + n); add(y, x + n); } if(x < 0 && y < 0) { add(-x + n, -y); add(-y + n, -x); } if(x < 0 && y > 0) { add(-x + n, y + n); add(y, -x); } } int tag1 = 0, tag2 = 0, tag0 = 0; for(int i = 1; i <= n; i ++) { memset(vis, 0, sizeof(vis)); dfs(i); int fl = 0; if(vis[i + n]) { memset(vis, 0, sizeof(vis)); dfs(i + n); fl = 1; if(vis[i]) { tag0 = 1; break; } for(int j = 1; j <= n; j ++) { if(j != i && vis[j]) { tag1 = 1; break; } } } memset(vis, 0, sizeof(vis)); dfs(i + n); if(vis[i]) { tag1 = 1; } else if(!fl) { for(int j = 1; j <= n; j ++) { if(j != i && vis[j]) { tag2 = 1; break; } } } } if(tag0) printf("0\n"); else if(tag1) printf("1\n"); else if(tag2) printf("2\n"); else printf("No Way\n"); } return 0; }
一道好题。（但是现在不想写题解了aaaa）
所以复制题解~
60分：
考虑这样一个贪心：
先从左往右扫，如果某一时刻不满足要求，则需要删除前面中某一个支持对方的人。我们贪心地选择删除当前时刻访问的人（肯定是支持对方），然后继续往后扫。
然后再从右往左扫，作相同的操作。
直观地理解是这样的：我们尽量删除靠右的人，使得从右往左扫时少删除一些人。
可以采用交换论证法证明这贪心是对的。
80-100：
首先我们可以发现从左往右扫完，从右往左扫的这个过程可以不用实现出来。只需要求出右端点开始的最小后缀和的相反数即可。
然后我们发现，如果两个询问区间拥有相同的左端点，则只需要作一次从左往右扫的工作。这使我们想到要离线化解决问题。
我们将询问按左端点排序，按照左端点从大到小的顺序求解询问。
如果已知从 i 开始向右扫需要删除那些结点，则从 i-1 开始向右扫需要删除那些结点可以快速求出。具体来说，如果i-1是支持者，则左数第一个被删除的结点与它抵消；如果i-1是反对者，则加入被删除的结点里。
该过程可以用栈维护。
通过在栈里面二分，我们可以知道区间[l, r]在从左往右扫时需要删除的结点数量。
现在问题就是求解以 r 为端点的最小后缀和。
这个东西可以用块状数组O(sqrt(N))维护（这就是80%算法的由来），更好的方法应该是用线段树O(log(N))维护
于是该题就在O((N+Q)logN)的时间复杂度内解决了。
#include<bits/stdc++.h> using namespace std; struct Tree { int mi, sum; } TR[500005*4]; int n, m; char s[500005]; void update(int nd) { TR[nd].mi = min(TR[nd << 1 | 1].mi, TR[nd << 1].mi + TR[nd << 1 | 1].sum); TR[nd].sum = TR[nd << 1].sum + TR[nd << 1 | 1].sum; } void build(int nd, int l, int r) { if(l == r) { TR[nd].mi = TR[nd].sum = 0; return ; } int mid = (l + r) >> 1; build(nd << 1, l, mid); build(nd << 1, mid + 1, r); update(nd); } void modify(int nd, int l, int r, int pos, int d) { if(l == r) { TR[nd].sum = d; TR[nd].mi = d; return ; } int mid = (l + r) >> 1; if(pos <= mid) modify(nd << 1, l, mid, pos, d); else modify(nd << 1 | 1, mid + 1, r, pos, d); update(nd); } Tree query(int nd, int l, int r, int pos) { if(l == r) return TR[nd]; int mid = (l + r) >> 1; if(pos <= mid) return query(nd << 1, l, mid, pos); else { Tree res = query(nd << 1 | 1, mid + 1, r, pos); res.mi = min(res.mi, res.sum + TR[nd << 1].mi); res.sum = res.sum + TR[nd << 1].sum; return res; } } vector < pair < int , int > > qus[500005]; int tp = 0, stk[500005], ans[500005]; int find(int pos) { int l = 1, r = tp, an = tp + 1; while(l <= r) { int mid = (l + r) >> 1; if(stk[mid] > pos) l = mid + 1; else an = mid, r = mid - 1; } return an; } int main() { freopen("sworder.in", "r", stdin); freopen("sworder.out", "w", stdout); scanf("%d", &n); scanf("%s", s + 1); scanf("%d", &m); for(int i = 1; i <= m; i ++) { int l, r; scanf("%d%d", &l, &r); qus[l].push_back(make_pair(r, i)); } build(1, 1, n); for(int i = n; i >= 1; i --) { if(s[i] == 'C') stk[++tp] = i; else { if(tp) { modify(1, 1, n, stk[tp], -1); stk[tp--] = 0; } modify(1, 1, n, i, 1); } for(int j = 0; j < qus[i].size(); j ++) { int pos = qus[i][j].first; int tmp = find(pos); ans[qus[i][j].second] = (tp - tmp + 1) - min(0, query(1, 1, n, pos).mi); } } for(int i = 1; i <= m; i ++) printf("%d\n", ans[i]); return 0; }