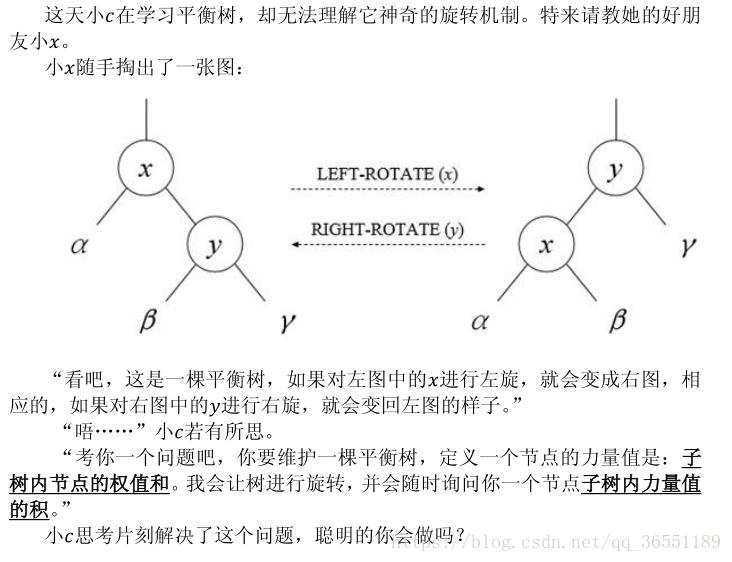
Problem
Input
Output
Hint
Solution
这道题刚看我以为打棵只会旋转、不会进行splay操作的splay,按它说的模拟就行了。
但是切了T1,滚来思考这道题时,我发现它每次旋转操作都会修改到点x和点y的力量值。设力量值为p,答案为t,则
和
旋转后(设y变成x的父亲),不仅仅是
和
会变动,y的所有祖先的t值都会变动。
于是,我又傻傻地想,每次旋转时,我们就把x和y旋到根,这样就只用变两个了。但是这样的话,把它们旋到根,有这么多旋转,都会变啊!而且树的形态还会改变啊!!
所以我苦思冥想,终于想到我其实可以用一棵splay维护树的形态,用另一个什么东西维护答案。我已开始以为可以链剖,但是发现树的形态会改变;所以又想到LCT,但是感觉不大可以。
这时,我想到以前做过的那些维护子树信息的题都是先将所有点按照dfs序(中序遍历)重标号,这样一来,以某个点为根的子树的那些编号就成了一个区间。
譬如假设有棵树:
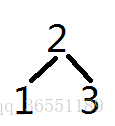
它按dfs序重标号了,所以2的子树是[1..3],1的子树是[1..1],3的子树是[3..3]之类。
那么,我们这题,它的树要旋转,那子树所含的编号区间会改变啊!
但是,我们知道,它这种旋转方式类似于splay,它会保持原树的中序遍历(splay的正确性就在于此),所以旋转之后每棵子树所含的编号依然是一个个区间。
譬如我们按照题目的方法右旋点2,则上图变成:
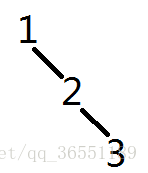
那么1的子树是[1..3],2的子树是[2..3],3的子树是[3..3]——依然是一段段连续的区间。
于是,我们可以用一棵只会旋转、不会进行splay操作的splay维护树的形态、每个节点的p值以及以每个节点为根的子树所含的编号区间(因为它每次操作只会改变x和y的信息);然后用一棵线段树维护区间p的乘积,拿来查询答案。而每次旋转只会修改两个p值,所以每次旋转只修改线段树中的两个点。
时间复杂度:
。
Code
#include <cstdio>
#include <cctype>
#include <cstring>
using namespace std;
#define dx dfn[x]
#define dl dfn[l[x]]
#define dr dfn[r[x]]
#define A v<<1
#define B A|1
#define ll long long
#define fo(i,a,b) for(i=a;i<=b;i++)
const int N=2e5+1;
const ll MO=1e9+7;
int i,n,Q,w[N],l[N],r[N],fa[N][2],top,X[N],x,dfn[N],time,son[N][2],fat[N],edge[N][2],opt;
ll v[N],p[N],f[N<<2],val;
void read(int &x)
{
char c=getchar(); x=0;
for(;!isdigit(c);c=getchar());
for(;isdigit(c);x=(x<<3)+(x<<1)+c-'0',c=getchar());
}
void scan()
{
read(n);read(Q);
fo(i,1,n)
{
read(w[i]);read(l[i]);read(r[i]);
fa[l[i]][0]=i,fa[l[i]][1]=0;
fa[r[i]][0]=i,fa[r[i]][1]=1;
}
}
inline bool so(int x){return son[fat[x]][1]==x;}
inline void link(int f,int x,bool d)
{
if(x)
son[fat[x]=f][d]=x;
else son[f][d]=0;
}
inline void update(int x)
{
p[x]=v[x];edge[x][0]=edge[x][1]=x;
int l=son[x][0],r=son[x][1];
if(l){p[x]=(p[x]+p[l])%MO;edge[x][0]=edge[l][0];}
if(r){p[x]=(p[x]+p[r])%MO;edge[x][1]=edge[r][1];}
}
//splay
void init()
{
X[top=1]=1;
while(top)
{
x=X[top];
if(l[x]&&!dl){X[++top]=l[x];continue;}
if(!dx)v[dx=++time]=w[x];
if(r[x]&&!dr){X[++top]=r[x];continue;}
link(dx,dl,0);
link(dx,dr,1);
update(dx);
top--;
}
}
struct node
{
int x,y;
};
ll ksm(ll x,int y)
{
ll ans=1;
for(;y;y>>=1)
{
if(y&1)ans=ans*x%MO;
x=x*x%MO;
}
return ans;
}
void maketree(int v,int l,int r)
{
if(l==r){f[v]=p[l];return;}
int mid=l+r>>1;
maketree(A,l,mid);
maketree(B,mid+1,r);
f[v]=f[A]*f[B]%MO;
}
void modify(int v,int l,int r,int x)
{
if(l==r)
{
val=val*ksm(f[v],MO-2)%MO;
f[v]=f[v]*val%MO;
return;
}
int mid=l+r>>1;
if(x<=mid)
modify(A,l,mid,x);
else modify(B,mid+1,r,x);
f[v]=f[v]*val%MO;
}
ll query(int v,int l,int r,int x,int y)
{
if(x<=l&&r<=y)return f[v];
int mid=l+r>>1;ll ans=1;
if(x<=mid)ans=query(A,l,mid,x,y);
if(y>mid)ans=ans*query(B,mid+1,r,x,y)%MO;
return ans;
}//segment tree
void rotate()
{
int a=son[x][!opt],y=son[x][opt],b=son[y][!opt],Y=son[y][opt],z=fat[x];
if(!y)return;
link(x,b,opt);
if(z)
link(z,y,so(x));
else fat[y]=0;
link(y,x,!opt);
update(x);val=p[x],modify(1,1,n,x);
update(y);val=p[y],modify(1,1,n,y);
}
void work()
{
fo(i,1,Q)
{
read(opt);read(x);x=dfn[x];
switch(opt)
{
case 0:rotate();break;
case 1:rotate();break;
case 2:printf("%lld\n",query(1,1,n,edge[x][0],edge[x][1]));break;
}
}
}
int main()
{
freopen("splay.in","r",stdin);
freopen("splay.out","w",stdout);
scan();
init();
maketree(1,1,n);
work();
}