CRNN原理

CRNN是《An End-to-End Trainable Neural Network for Image-based Sequence Recognition and Its Application to Scene Text Recognition》中提出的模型，解决图像中文字识别问题。

论文地址：https://arxiv.org/abs/1507.05717

github地址：https://github.com/bgshih/crnn

1：结构图

主要包括：卷积层（CNN），循环层（RNN），转录层（CTC）

2：整个网络模型的特点

可以直接从序列标签学习，不用给每个字符打标签，只需要给一个图片打一个序列标签，例如：图片中是“abc123”，标签即是“abc123”，不用给每个字符单独打标签。
利用CNN提取的图片特征
利用RNN训练的输入的特征序列，输出的是一个序列标签
对要训练的图片没有长度限制，但是要将图片的高度归一化。
参数少
虽然结合了CNN和RNN，但最后用一个loss函数（CTC LOSS），实现了端到端的训练。

3：CRNN中的重点，也就是CTC(connectionist temporal classification)原文出自《Connectionist Temporal Classification: Labelling Unsegmented Sequence Data with Recurrent Neural Networks》

首先，CRNN第一步是将训练的图片送入到CNNji进行卷积提取特征，得到feature map

然后，将feature map的每一列（这里先简化处理，认为一列就是一个LSTM时间序列，CRNN网络结构后面分析）或者每几列作为一个时间序列输入特征，送入RNN（双向LSTM）

先看一下流程图：

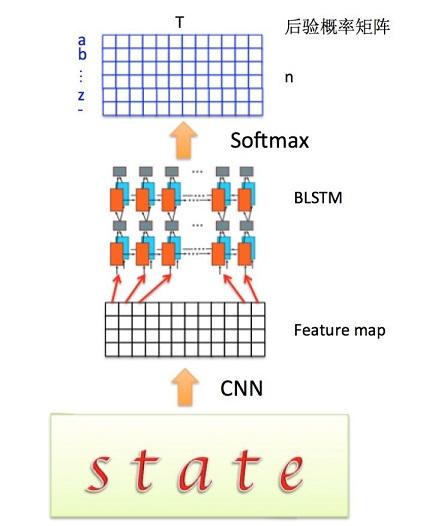
preview

CNN feature map

假设CNN得到的feature map 大小为 $m*T$ ，下文得到的时间序列 $t$ 都从 $t = 1$ 开始，即 $1\leq t\leq T$ 。

则输入到RNN中的时间序列定义为： $x = (x^{1},x^{2},x^{3},......,x^{T})$ ，

其中每一列为：

$x^{t} = ({x_{1}}^{t},{x_{2}}^{t},{x_{3}}^{t},......,{x_{m}}^{t})$

RNN（双向LSTM）

LSTM的每个时间片后接一个softmax，输出的是一个后验概率矩阵，大小为n*T，T代表时间序列总共T列，n代表有词典中有n个标签，定义为： $y = (y^{1},y^{2},y^{3},......,y^{T})$

其中每一列为：

$y^{t} = ({y_{1}}^{t},{y_{2}}^{t},{y_{3}}^{t},......,{y_{n}}^{t})$

由于是得到的是概率，所以每列的所有字符标签的概率之和为1，即 $\sum_{i = 1}^{n} {y_{i}}^{t} = 1$ ，那取每列的最大值，就能得到每一列输出字符的类别，即对每列进行 $argmax()$ 操作。

将该LSTM网络看成一个映射 $y = N_{w}(x)$ ，其中w为LSTM的参数。m*T 的CNN得到的feature map，输入经LSTM后输出为 n*T，所以 $N_{w}$ 是做了如下变换： $N_w: (R^{m})^T\rightarrow (R^n)^T$

假设原始的字符标签为L = {a,b,c,......,x,y,z}的26和字母，由于要加一个默认的空格字符blank（作用类似于目标检测中的默认的背景标签），此时的新的字符标签为L‘。

定义B变换：

$B:L'^T \rightarrow L$ ，表示简单的压缩

说明：假设T = 12，也就是说有12列，路径为 $\pi$ ，路径的长度就是T。

$B(\pi_1)=B(--s\ t\ t\ a-t---e)=state\\$ $B(\pi_2)=B(s\ s\ t-a\ a\ a-t\ e\ e-)=state\\$ $B(\pi_3)=B(--s\ t\ t\ a\ a-t\ e\ e-)=state\\$ $B(\pi_4)=B(s\ s\ t-a\ a-t---e)=state\\$

$B(\pi_5)=B(-\ s\ t\ a-a\ t\ t\ e-\ e-)=staatee\\$

如上所示5条路径，看出规律有：若两个字符之间有空格blank 时，则不合并，若没有空格时，相同字符合并为一个。

当获得LSTM经过softmax（注意是softmax不是softmax loss，因为这里用的是CTC loss）得到字符概率得分矩阵后，经argmax()操作后得到的输出y，经过B变换后，即可获得输出结果，显然B变换不是一一映射的关系。现在我们能通过feature map用每列当做x输入到RNN中，得到概率矩阵，并argmax()操作得到输出，然后用这一步的输出经过B变换规则得到最终的字符预测输出。但是这样的输出和当时的输入的列数不一样（明显不一样，也就是发生了不对齐的现象。），训练需要反向传播来更新参数，所以，怎样利用得到的预测输出来计算loss呢。

如果输出是用的softmax得到的概率矩阵，每列对应的是输出 $y'$ 都对应标签中的一个字符。那么训练时候每张样本图片都需要标记出每个字符在图片中的位置，再通过CNN感受野对齐到Feature map的每一列，如图3，才能进行训练。

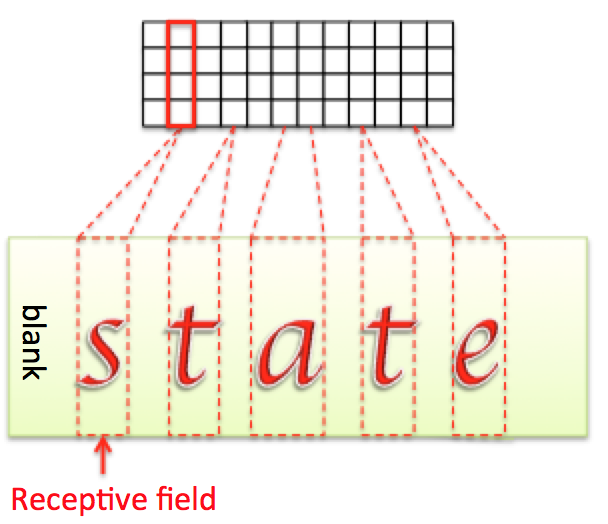
preview

在实际应用中，标记这样的对齐样本非常困难，工作量非常大，所以CTC提出了一种不需要对齐的Loss计算方法，用于训练网络。

先来计算一下，路径的数目：假设T = 30，最后的输出为“state”，五个字符，共有 ${C_{29}}^{5}\approx 120000$ 条路径可以被压缩成【state】。路径数目的计算公式为 ${C_{T-1}}^{count(y)}$ 。

CTC的做法:

对于LSTM给定输入 $x$ 的情况下，输出为 $l$ 的概率为：

$p(l|x)=\sum_{\pi \in B^{-1}(l)}{}p(\pi|x)\\$

上边的式子说明：输入 $x$ 的情况下，输出为 $l$ 的概率为：条件为输入为 $x$ ，进过B变换后输出为 $l$ 的所有路径的概率之和。

那么每一条路径的概率怎么算呢： $p(\pi|x)=\prod_{t=1}^{T}y_{\pi_t}^t\ ,\ \forall \pi \in L'^T\\$

上边的式子说明：每一条路径的概率为该条路径的每一个时刻的输出的连乘。

我们的目标函数就相当于是 $max\ p(l|x) = max \sum_{\pi \in B^{-1}(l)}^{ }p(\pi |x)$

但是路径数目庞大，是无法直接计算的，所以CTC方法中借用了HMM中向前向后算法（forward-backward algorithm）来计算。

preview

CTC的训练过程，本质上是通过梯度 $\frac{\partial p(l|x)}{\partial w}$ 调整LSTM的参数 $w$ ，使得对于输入样本为 $\pi \in B^{-1}(l)$ 时有 $p(l|x)$ 取得最大。

定义所有经 $B$ 变换后结果是 $l$ 且在 $t$ 时刻结果为 $l_k$ （记为 $\pi_t=l_k$ ）的路径集合为 $\{\pi|\pi\in B^{-1}(l),\pi_t=l_k\}$ 。

求导：

$\frac{\partial p(l|x)}{\partial y_k^t}=\frac{\partial \sum_{\pi \in B^{-1}(l)}{}p(\pi|x)}{\partial y_k^t}$

$=\frac{\partial \sum_{\pi \in B^{-1}(l),\pi_t=l_k}{}p(\pi|x)}{\partial y_k^t}+\frac{\partial \sum_{\pi \in B^{-1}(l),\pi_t\ne l_k}{}p(\pi|x)}{\partial y_k^t}$

注意上式中第二项与 $y_k^t$ 无关，所以：

$\frac{\partial p(l|x)}{\partial y_k^t}=\frac{\partial \sum_{\pi \in B^{-1}(l),\pi_t=l_k}{}p(\pi|x)}{\partial y_k^t}$

首先来理解一下上边的式子： $y_k^t$ 是 $t$ 时刻输出字符为 $k$ 的概率。上边的求导公式中的 $\partial \sum\ _{\pi\in B^{-1}(l),\pi _{t} = l_{k}}\ p(\pi |x)$ 理解为：由于总归的路线数目巨大，我这里求导只需要计算经过 $t$ 时刻输出字符为 $k$ 的所有路径。示意图如下：

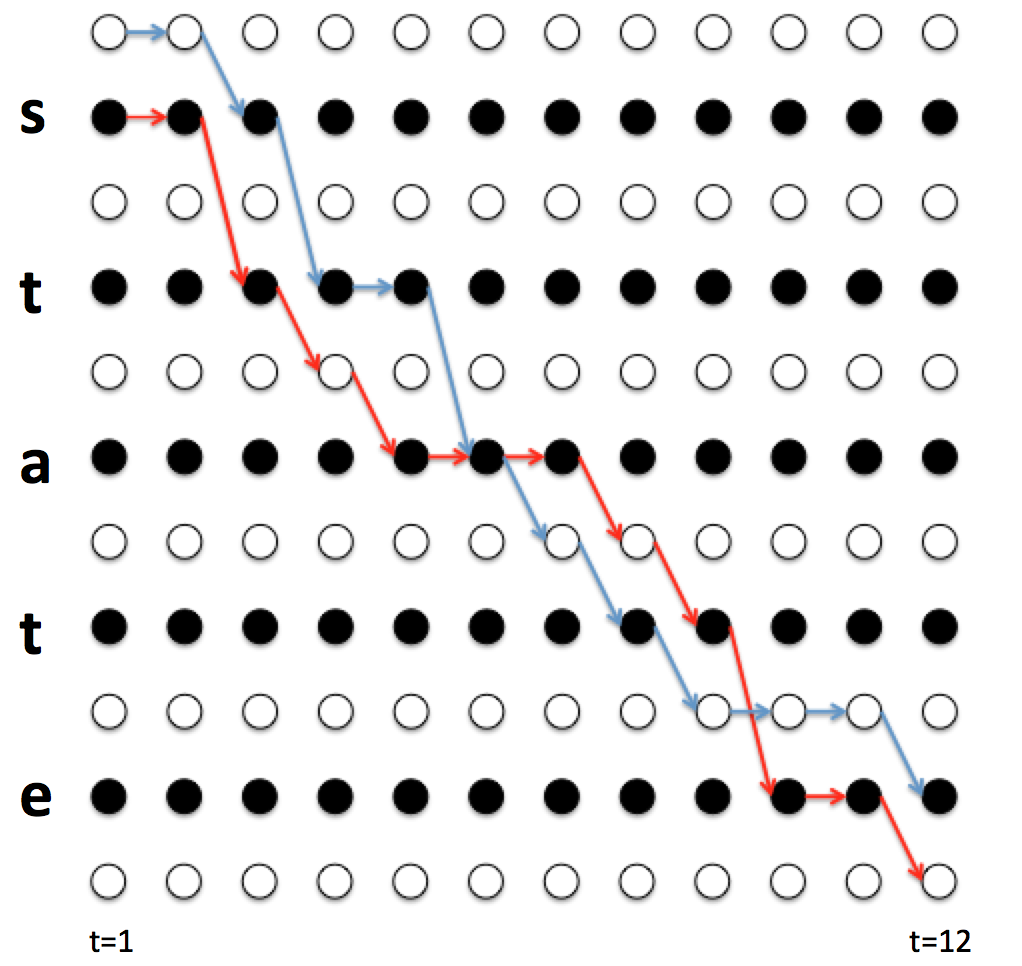
preview

假设 $y_k^t$ 是t=6时刻，k = a字符。那么依据上图经过这个点的路径有两条（没画出来的还有好几条），假设总共有四条路径经过该点，分别为 $\pi_1 ,\pi_2,\pi_3,\pi_4$ ，所有类似于 $\pi_1 ,\pi_2,\pi_3,\pi_4$ 经过 $B$ 变换后结果是 $l=state$ 且在 $\pi_6=a$ 的路径集合表示为 $\{\pi|\pi\in B^{-1}(l),\pi_6=a\}$ 。

观察 $\pi_1 ,\pi_2,\pi_3,\pi_4$ 。记 $\pi_1$ 蓝色为 $b$ ， $\pi_2$ 红色路径为 $r$ 。那么 $\pi_3,\pi_4$ 可以表示：

$\pi _{1} = b = b_{1:5} + a_{6} + b_{7:12}$

$\pi _{2} = r = r_{1:5} + a_{6} + r_{7:12}$

$\pi_3,\pi_4$ 可以是 $\pi_1,\pi_2$ 经过交叉点后互换下半段路径：

$\pi_3=b_{1:5}+a_6+r_{7:12}\\$ $\pi_4=r_{1:5}+a_6+b_{7:12}\\$

计算：

$\frac{\partial p(l|x)}{\partial y_a^6}=\frac{\partial \sum_{\pi \in B^{-1}(l),\pi_6=a}{}p(\pi|x)}{\partial y_a^6}=\frac{\partial p(\pi_1|x)+\partial p(\pi_2|x)+\partial p(\pi_3|x)+\partial p(\pi_4|x)...}{\partial y_a^6}\\$

为了观察规律，单独计算 $p(\pi_1|x)+p(\pi_2|x)+p(\pi_3|x)+p(\pi_4|x)$ 。

$p(\pi_1|x)+p(\pi_2|x)+p(\pi_3|x)+p(\pi_4|x)$

$=y_-^1\cdot y_-^2\cdot y_s^3\cdot y_t^4\cdot y_t^5\cdot y_a^6\cdot y_-^7\cdot y_t^8\cdot y_-^9\cdot y_-^{10}\cdot y_-^{11}\cdot y_e^{12}$

$\ \ +y_s^1\cdot y_s^2\cdot y_t^3\cdot y_-^4\cdot y_a^5\cdot y_a^6\cdot y_a^7\cdot y_-^8\cdot y_t^9\cdot y_e^{10}\cdot y_e^{11}\cdot y_-^{12}$

$\ \ +y_-^1\cdot y_-^2\cdot y_s^3\cdot y_t^4\cdot y_t^5\cdot y_a^6\cdot y_a^7\cdot y_-^8\cdot y_t^9\cdot y_e^{10}\cdot y_e^{11}\cdot y_-^{12}$

$\ \ +y_s^1\cdot y_s^2\cdot y_t^3\cdot y_-^4\cdot y_a^5\cdot y_a^6\cdot y_-^7\cdot y_t^8\cdot y_-^9\cdot y_-^{10}\cdot y_-^{11}\cdot y_e^{12}$

令：

$forward=p(b_{1:5}+r_{1:5}|x)=y_-^1\cdot y_-^2\cdot y_s^3\cdot y_t^4\cdot y_t^5+y_s^1\cdot y_s^2\cdot y_t^3\cdot y_-^4\cdot y_a^5$

$backward=p(b_{7:12}+r_{7:12}|x)=y_-^7\cdot y_t^8\cdot y_-^9\cdot y_-^{10}\cdot y_-^{11}\cdot y_e^{12}+y_a^7\cdot y_-^8\cdot y_t^9\cdot y_e^{10}\cdot y_e^{11}\cdot y_-^{12}$

那么 $p(\pi_1|x)+p(\pi_2|x)+p(\pi_3|x)+p(\pi_4|x)$ 可以表示为：

$p(\pi_1|x)+p(\pi_2|x)+p(\pi_3|x)+p(\pi_4|x)={forward} \cdot y_a^t \cdot {backward}\\$

推广一下，所有经过 $B$ 变换为 $l$ 且 $\pi_6=a$ 的路径（即 $\{\pi|\pi \in B^{-1}(l),\pi_6=a\}$ ）可以写成如下形式：

$\sum_{\pi \in B^{-1}(l),\pi_6=a}p(\pi|x)={forward} \cdot y_a^t \cdot {backward}\\$

进一步推广，所有经过 $B$ 变换为 $l$ 且 $\pi_t=l_k$ 的路径（即 $\{\pi|\pi \in B^{-1}(l),\pi_t=l_k\}$ ）也都可以写作：

$\sum_{\pi \in B^{-1}(l),\pi_t=l_k}p(\pi|x)={forward} \cdot y_{l_k}^t \cdot {backward}\\$

所以，定义forward $\alpha_t(s)$ ：

对于一个长度为 $T$ 的路径 $\pi$ ，其中 $\pi_{1:t}$ 代表该路径前 $t$ 个字符， $\pi_{t:T}$ 代表后 $T-t$ 个字符。

$\alpha_t(s)=\sum_{\pi \in B(\pi_{1:t})=l_{1:s}}{\prod_{t'=1}^{t}y_{\pi_{t'}}^{t'}}\\$

其中 $\pi \in B(\pi_{1:t})=l_{1:s}$ 表示前 $t$ 个字符 $\pi_{1:t}$ 经过 $B$ 变换为的 $l_{1:s}$ 的前半段子路径。

观察图7会发现对于 $\alpha_6(a)$ 有如下递推关系：

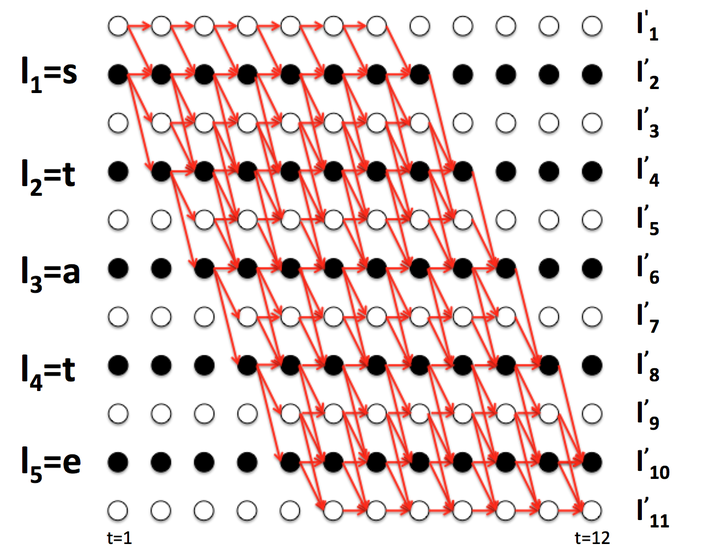
图6

$\alpha_6(a)=(\alpha_5(a)+\alpha_5(t)+\alpha_5(-))\cdot y_a^6\\$

那么更一般的：

$\alpha_t(l'_k)=(\alpha_{t-1}(l'_k)+\alpha_{t-1}(l'_{k-1})+\alpha_{t-1}(-))\cdot y_{l'_k}^t\\$

上边的怎么理解呢：

蓝色矩形标记的时刻字符点，它的forward受到它前一个时刻的三个方向（黄色箭头）的预测。所以有：

$\alpha_t(l'_k)=(\alpha_{t-1}(l'_k)+\alpha_{t-1}(l'_{k-1})+\alpha_{t-1}(-))\cdot y_{l'_k}^t\\$

同样，定义backword $\beta_t(s)$ ：

$\beta_t(s)=\sum_{\pi \in B(\pi_{t:T})=l_{s:|l|}}{\prod_{t'=t}^{T}y_{\pi_{t'}}^{t'}}\\$

根据

同理对于 $\beta_t(s)$ 有如下递推关系：

$\beta_t(l'_k)=(\beta_{t+1}(l'_k)+\beta_{t+1}(l'_{k+1})+\beta_{t+1}(-))\cdot y_{l'_k}^t\\$

那么forward和backward相乘有：

$\alpha_t(l'_k)\beta_t(l'_k))=\sum_{\pi\in B^{-1}(l),\pi_t=l'_k}y_{l'_k}^t\prod_{t=1}^{T}y_{\pi_t}^{t}\\$

或：

$\alpha_t(l_k)\beta_t(l_k))=\sum_{\pi\in B^{-1}(l),\pi_t=l_k}y_{l_k}^t\prod_{t=1}^{T}y_{\pi_t}^{t}\\$

注意， $y_{l_k}^t与y_{l’_k}^t$ 可以通过图6的关系对应，如 $y_{l_1}^t=y_{l’_2}^t$ ， $y_{l_2}^t=y_{l’_4}^t$ 。

对比 $p(l|x)$ :

$p(l|x)=\sum_{\pi \in B^{-1}(l)}{}p(\pi|x)=\sum_{\pi \in B^{-1}(l)}\prod_{t=1}^{T}y_{\pi_t}^t\\$

可以得到：

$p(l|x) = \sum_{\pi \in B^{-1}(l),\pi_t=l_k}{}\frac{\alpha_t(l_k)\beta_t(l_k)}{y_{l_k}^t}\\$

或：

$\alpha_t(l_k)\beta_t(l_k))=\sum_{\pi\in B^{-1}(l),\pi_t=l_k}y_{l_k}^t\prod_{t=1}^{T}y_{\pi_t}^{t}\\$

训练CTC

对于LSTM，有训练集合 $S=\{(x_1,z_1),(x_1,z_1),...,(x_N,z_N)\}$ ，其中 $x$ 是图片经过CNN计算获得的Feature map， $z$ 是图片对应的ocr字符label（label里面没有blank字符）。

现在我们要做的事情就是：通过梯度 $\frac{\partial p(l|x)}{\partial w}$ 调整LSTM的参数 $w$ ，使得对于输入样本为 $\pi \in B^{-1}(z)$ 时有 $p(l|x)$ 取得最大。所以如何计算梯度才是核心。

单独来看LSTM输出 $y$ 矩阵中的某一个值 $y_k^t$ （注意 $y_k^t$ 与 $y_{l_k}^t$ 含义相同，都是在 $t$ 时 $\pi_t=l_k$ 的概率）：

$\frac{\partial p(l|x)}{\partial y_k^t}=\frac{\partial \sum_{\pi \in B^{-1}(l),\pi_t=l_k}{}\frac{\alpha_t(l_k)\beta_t(l_k)}{y_{l_k}^t}}{\partial y_{l_k}^t}=\frac{\sum_{\pi \in B^{-1}(l),\pi_t=l_k}\alpha_t(l_k)\beta_t(l_k)}{(y_{l_k}^t)^2}\\$

获得梯度 $\frac{\partial p(l|x)}{\partial y_k^t}$ 后就好办了，其中的 $\alpha_t(l_k)\beta_t(l_k)$ 可以通过递推快速计算，那么梯度下降算法你懂的。

CTC总结

CTC是一种Loss计算方法，用CTC代替Softmax Loss，训练样本无需对齐。

CTC特点：

同时引入blank字符，解决有些位置没有字符的问题
通过递推，快速计算梯度

猜你喜欢