最大流
Ford-Fulkerson算法：
（1）只利用满足f(e)<c(c)的e或者满足f(e)>0的e对应的反向边rev(e)，寻找一条s到t的路径。
（2）如果不存在满足条件的路径，则结束。否则，沿着该路径尽可能地增加流，返回第（1）步
1 #include <cstdio> 2 #include <vector> 3 #include <cstring> 4 5 using namespace std; 6 7 struct edge 8 { 9 int to; 10 int cap; 11 int rev; 12 }; 13 const int INF=0x3f3f3f3f; 14 const int MAX_V=1000; 15 vector<edge> G[MAX_V]; 16 bool used[MAX_V]; 17 18 void add_edge(int from, int to, int cap) 19 { 20 edge e; 21 e.to=to; e.cap=cap; e.rev=G[to].size(); 22 G[from].push_back(e); 23 e.to=from; e.cap=0; e.rev=G[from].size()-1; 24 G[to].push_back(e); 25 } 26 27 int dfs(int v, int t, int f) 28 { 29 if (v==t) return f; 30 used[v]=true; 31 for (int i=0; i<G[v].size(); i++) 32 { 33 edge &e=G[v][i]; 34 if (!used[e.to] && e.cap>0) 35 { 36 int d=dfs(e.to, t, min(f, e.cap)); 37 if (d>0) 38 { 39 e.cap-=d; 40 G[e.to][e.rev].cap+=d; 41 return d; 42 } 43 } 44 } 45 return 0; 46 } 47 48 int max_flow(int s, int t) 49 { 50 int flow=0; 51 for (;;) 52 { 53 memset(used, 0, sizeof(used)); 54 int f=dfs(s, t, INF); 55 if (f==0) return flow; 56 flow+=f; 57 } 58 }
记最大流的流量为F，Ford-Fulkerson算法最多进行F次深度优先搜索，所以其复杂度为O(F|E|)。但这是一个很松的上界，达到这种最坏复杂度的情况几乎不存在。
最小割
最大流最小割定理：最大流等于最小割
定理证明：
①首先考虑任意的s-t流f和任意的s-t割(S,V\S)。因为有(f的流量)=(s的出边的总流量)，而对v∈S\{s}又有(v的出边的总流量)=(v的入边的总流量)，所以有(f的流量)=(S的出边的总流量)-(S的入边的总流量)，由此可知(f的流量)≤(割的容量)。
②接下来，考虑通过Ford-Fulkerson算法所求的的f'，记流量f'对应的残余网络中从s可达的顶点v组成的集合S，因为f'对应的残余网络中不存在s-t路径，因此(S,V\S)就是一个s-t割，此外，根据S的定义，对包含在割中的边e应该有f'(e)=c(e)，而对从V\S到S的边e应该有f'(e)=0。因此，(f的流量)=(S的出边的总流量)-(S的入边的总流量)=(割的容量)，再由之前的不等式可以知道，f'即为最大流。
最大流的各种变体
- 多个源点和汇点的情况
如果有多个源点和汇点，并且它们都有对应的最大流出容量和流入容量限制时，只要增加一个超级源点s和一个超级汇点t，从s向每个源点连一条容量为对应最大流出容量的边，，从每个汇点向t连一条容量为对应最大流入容量的边。
（如果源和汇之间存在对应关系，即从不同源点流出的流要流入指定的汇点，是无法求解的，这种情况被称为多物网络流问题，尚无已知的高效算法） - 无向图的情况
把无向图中容量为c的一条边当作有向图中两个方向各有一条容量为c的两条边。 - 顶点上也有容量限制的情况
图中不光边上有流量限制，途中经过的顶点也有总流入量和总流出量的限制的情况，此时，把每个顶点拆成两个，拆点之后得到入顶点和出顶点，将指向原先顶点的边改成指向入顶点，将从原先顶点指出的边改成从顶点指出，并且再从入顶点向出顶点连容量为原先定点容量限制的边，就可以把顶点上的容量限制转为边上的容量限制了。 - 有最小流量限制的情况
不光有最大流量限制c(e)，还有最小流量限制b(e)的情况(b(e)≤f(e)≤c(e))。令f'(e)=f(e)-c(e)，就可以转为只有最大流量限制0≤f'(e)≤c(e)-b(e)的情况。而此时顶点对应的总流入量和总流出量变为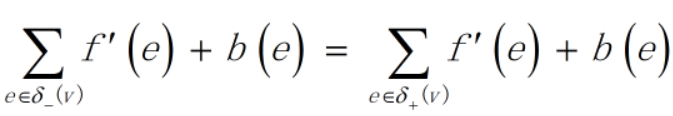
这可以看成是有一个最大流出量为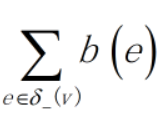
的源点和一个最大流入量为
的汇点与之相连 。于是，可以增加新的源点S和汇点T，对于每条边e=(u,v)，令c'(e)=c(e)-b(e)，并从S向v连一条容量为b(e)的边，从u向T连一条容量为b(e)的边，并从S向s连一条容量为∞的边，从t向T连一条容量为∞的边，这样就转为了没有最小流量限制的情况，如果新图中从S到T的最大流流量为F'，那么原图中的最大流流量为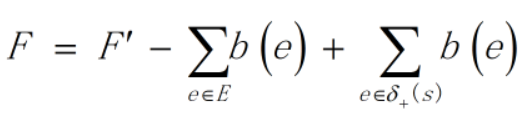
。不过，原图的下限限制未必能够满足时，应该在S与s，T与t之间连边之前，检查从S到T的最大流流量是否为
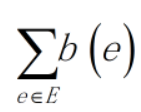，如果不是满流，则原上下界网络流问题没有可行解。 -
图发生部分变化的情况
在某些问题中，求完某个图的最大流之后，需要对原图中的一部分做一些变化，再对新图求最大流，这这种情况下，有时不需要重新计算最大流，而可以重复利用前一步的结果，高效地求出新的最大流。
①边e=(u,v)容量增加的情况，只要在原图的最大流f的基础上，不断寻找增广路增广，就可以求得新图的最大流。多条边的容量同时增加的情况也一样。
②边e=(u,v)容量减小1的情况，如果原图的最大流中，有f(e)≤c(e)-1的话，那么它也是新图的最大流，否则，如果f(e)=c(e)，为了让新图满足流量限制，需要将多出部分的流退回去。假如f的残余网络中存在从u到v的路径，那么就可以沿这条路径增广1并把f(e)减小1，而保持最大流流量不变。否则，需要找t→v和u→s的路径，沿它们增广1并把f(e)减小1之后，最大流流量也减小1。当有多条边的容量同时减小或减小量不止1时，也可以类似处理。在求字典序最小的最大流之类的问题中会用到这种技巧。 - 容量为负数的情况
一般情况下，不能利用最大流算法来求解，也没有已知的有效算法，但有些情况下，可以采取适当的变形而避免出现负容量边。
更高效的最大流算法Dinic
Dinic算法总是寻找最短的增广路，并沿着它增广。因为最短增广路的长度在增广过程中始终不会变短，所以无需每次都通过宽度优先搜索来寻找最短增广路。我们可以先进行一次宽度优先搜索，然后考虑由近距离顶点指向远距离顶点的边所组成的分层图，在上面进行深度优先搜索寻找最短增广路。如果在分层图上找不到新的增广路了（此时我们得到了分层图所对应的阻塞流），则说明最短增广路的长度确实变长了，或不存在增广路了，于是重新通过宽度优先搜索构造新的分层图。每一步构造分层图的复杂度为O(|E|)，而每一步完成之后最短增广路的长度都会至少增加1，由于增广路的长度不会超过|V|-1，因此最多重复O(|V|)步就可以了。另外，在每次对分层图进行深度优先搜索寻找增广路时，如果避免对一条没有用的边进行多次检查（这个优化称作当前弧优化），就可以保证复杂度为O(|E||V|)，这样总的复杂度就是O(|E||V|2)。实际应用中速度非常快，很多时候即便图的规模比较大也没有问题。
1 #include <cstdio> 2 #include <vector> 3 #include <queue> 4 #include <cstring> 5 6 using namespace std; 7 8 const int INF=0x3f3f3f3f; 9 const int MAX_V=10000; 10 struct edge 11 { 12 int to; 13 int cap; 14 int rev; 15 }; 16 vector<edge> G[MAX_V]; 17 int level[MAX_V]; 18 int iter[MAX_V]; 19 20 void add_edge(int from, int to, int cap) 21 { 22 edge e; 23 e.to=to;e.cap=cap;e.rev=G[to].size(); 24 G[from].push_back(e); 25 e.to=from;e.cap=0;e.rev=G[from].size()-1; 26 G[to].push_back(e); 27 } 28 29 void bfs(int s) 30 { 31 memset(level, -1, sizeof(level)); 32 queue<int> que; 33 level[s]=0; 34 que.push(s); 35 while (!que.empty()) 36 { 37 int v=que.front();que.pop(); 38 for (int i=0; i<G[v].size(); i++) 39 { 40 edge &e=G[v][i]; 41 if (e.cap>0 && level[e.to]<0) 42 { 43 level[e.to]=level[v]+1; 44 que.push(e.to); 45 } 46 } 47 } 48 } 49 50 int dfs(int v, int t, int f) 51 { 52 if (v==t) return f; 53 for (int &i=iter[v]; i<G[v].size(); i++) 54 { 55 edge &e=G[v][i]; 56 if (e.cap>0 && level[v]<level[e.to]) 57 { 58 int d=dfs(e.to, t, min(f, e.cap)); 59 if (d>0) 60 { 61 e.cap-=d; 62 G[e.to][e.rev].cap+=d; 63 } 64 } 65 } 66 return 0; 67 } 68 69 int max_flow(int s, int t) 70 { 71 int flow=0; 72 for (;;) 73 { 74 bfs(s); 75 if (level[t]<0) return flow; 76 memset(iter, 0, sizeof(iter)); 77 int f; 78 while ((f=dfs(s, t, INF))>0) 79 { 80 flow+=f; 81 } 82 } 83 }
二分图匹配
无向二分图G=(U∪V,E)：∀(u,v)∈E,u∈U，v∈V
求：G中满足两两不含公共端点的边集合M⊆E的基数|M|的最大值。
两两不含公共端点的边集合M称为匹配，而元素最多的M则称为最大匹配。当最大匹配的匹配数满足2|M|=|V|时，又称为完美匹配（即所有顶点都是匹配点）。特别地，二分图中的匹配又称为二分图匹配。二分图匹配常常在指派问题的模型中出现。
实际上，可以将二分图最大匹配问题看成是最大流问题的一种特殊情况，不妨对原图作如下变形：将原图中的所有无向边e改成有向边，方向从U到V，容量为1。增加源点s和汇点t，从s向所有的顶点u∈U连一条容量为1的边，从所有的顶点v∈V向t连一条容量为1的边。
这样变形得到的新图G'中最大s-t流的流量就是原二分图G中最大匹配的匹配数，而U-V之间流量为正的边集合就是最大匹配，该算法的复杂度为O(|V||E|)。
1 int N,K; 2 bool can[MAX_N][MAX_K]; 3 4 void solve() 5 { 6 //0~N-1:U集合 7 //N~N+K-1:V集合 8 int s=N+K, t=s+1; 9 for (int i=0; i<N; i++) 10 { 11 add_edge(s, i, 1); 12 } 13 for (int i=0; i<K; i++) 14 { 15 add_edge(N+i, t, 1); 16 } 17 for (int i=0; i<N; i++) 18 { 19 for (int j=0; j<K; j++) 20 { 21 if (can[i][j]) 22 { 23 add_edge(i, N+j, 1); 24 } 25 } 26 } 27 printf("%d\n", maxflow(s,t)); 28 }
利用所有边的容量都是1以及二分图的性质，我们还可以像下面这样将二分图最大匹配算法（匈牙利算法）更简单地实现。
（附上：二分图匹配——匈牙利算法）
1 int V; 2 vector<int> G[MAX_V]; 3 int match[MAX_V]; 4 bool used[MAX_V]; 5 6 void add_edge(int u, int v) 7 { 8 G[u].push_back(v); 9 G[u].push_back(u); 10 } 11 12 bool dfs(int v) 13 { 14 used[v]=true; 15 for (int i=0; i<G[v].size(); i++) 16 { 17 int u=G[v][i], w=match[u]; 18 if (w<0 || !used[w] && dfs(w)) 19 { 20 match[v]=u; 21 match[u]=v; 22 return true; 23 } 24 } 25 return false; 26 } 27 28 int bipartite_matching() 29 { 30 int res=0; 31 memset(match, -1, sizeof(match)); 32 for (int v=0; v<V; v++) 33 { 34 if (match[v]<0) 35 { 36 memset(used, 0, sizeof(used)); 37 if (dfs(v)) 38 { 39 res++; 40 } 41 } 42 } 43 return res; 44 }
一般图匹配
不能像二分图一样转为最大流问题处理。
求解一般图匹配问题可以使用Edmonds算法等高效算法，但实现较为复杂（附上：一般图最大匹配——带花树算法）
Tutte矩阵做法：
对无向图G=<V, E>的每一条边随意赋予方向得到有向图G'=<V, E'>，并对每条边e∈E'都关联一个变量xe。
Tutte矩阵是一个如下定义的V*V的矩阵T=(tu,v)：
tu,v=① x(u,v) ((u,v)∈E')
② -x(u,v) ((v,u)∈E')
③0 (其它)
可以证明，此时：G没有完美匹配↔行列式det(T)恒等于0
证明方法：行列式的值可展开为所有排列对应的项的和，将排列看成一个有向图，如果该图包含奇圈的话，那么这个排列所对应的项就会和将奇圈反向后的排列所对应的项相互抵消，因此只要考虑由偶圈组成的排列就好了。如果其中有非零项的话，只要对应的偶圈上间隔取边就得到了一个完美匹配。并且，该项不会被其它任何项相互抵消。反之，如果存在完美匹配的话，那么通过交换相互匹配的点对而得到的排列所对应的项非零，且该项不会被其它任何项相互抵消。
由此还可以证明，T的秩等于最大匹配的顶点数。
于是，可以利用随机算法，将随机数带入xe，从而求得一般图的匹配数。
匹配、边覆盖、独立集和顶点覆盖
记图G=(V, E)
匹配：在G中两两没有公共端点的边集合M⊆E
边覆盖：G中的任意顶点都至少是F中某条边的端点的边集合F⊆E
独立集：在G中两两互不相连的顶点集合S⊆V
顶点覆盖：G中的任意边都有至少一个端点属于S的顶点集合S⊆V
关系：
(a) 对于不存在孤立点的图，|最大匹配|+|最小边覆盖|=|V|
证明：通过向最大匹配中加边而得到最小边覆盖
(b) |最大独立集|+|最小顶点覆盖|=|V|
证明：X⊆V是G的独立集↔V\X是G的顶点覆盖
(c)对于二分图，|最大匹配|=|最小顶点覆盖|
证明：对于二分图G=(U∪V，E)，在通过最大流求解最大匹配所得到的残留网络中，令S=(从s不可达的属于U的顶点)∪(从s可达的属于V的顶点)，则S就是G的一个最小顶点覆盖。
最小费用流
算法：在残余网络上总是沿着最短路增广，残余网络中的反向边的费用应该是原边费用的相反数，有负权边，用Bellman-Ford.
如何判断某个流的费用是最小的？
某个流量的流f，假设有同样流量而费用更小的流f'，流f'-f中所有顶点的流入量=流出量，即它是由若干圈组成的。因为流f'-f的费用是负的，所以，在这些圈中，至少存在一个负圈：
f是最小费用流↔残余网络中没有负圈
设流量为i的流fi是具有相同流量的流中费用最小的。首先，对于流量为0的流f0，其参与网络就是原图，只要原图不含负圈，那么f0就是流量为0的最小费用流。假设流量为i的流fi是最小费用流，并且下一步我们求得了流量为i+1的流fi+1。此时fi+1-fi就是fi对应的残余网络中s到t的最短路。如果fi+1不是最小费用流，那么就存在费用更小的流fi+1'，fi+1’-fi中除了s和t以外的顶点的流入量=流出量，因而是由一条从s到t的路径和若干圈组成的。又有fi+1-fi是一条从s到t的最短路，而fi+1’的费用比fi+1还要小，所以fi+1’-fi中至少含有一个负圈，这与fi是最小费用流矛盾，所以，fi+1也是最小费用流，根据归纳法，对任意的i都有fi是最小费用流。
另外，由最大流算法的正确性，如果原图存在流量不小于F的流的话，那么这个算法也能够得到流量为F的流。
优化：导入势的概念，给每个顶点赋予一个标号h(v)，在势的基础上，将边e=(u,v)的长度变为d'(e)=d(e)+h(u)-h(v)。于是从d'中的s-t路径的长度中减去常数h(s)-h(t)，就得到了d中对应路径的长度，因此d'中的最短路也就是d中的最短路，合理取势，使得所有e都有d'(e)≥0，就可以用Dijkstra求最短路，从而得到d的最短路。对于任意不含负圈的图，我们可以通过取h(v)=(s到v的最短距离)做到这一点。这是因为：（s到v的最短距离）≤（s到u的最短距离）+ d(e)，于是d'(e)=d(e)+h(u)-h(v)≥0。
依次更新流量为i的最小费用流fi及其对应的势hi，来求出最小费用流。定义：
fi(e)：流量为i 的最小费用流中边e的流量
hi(v)：fi的残余网络中s到v的最短距离
di(e)：考虑势hi后边的长度
如果图中不含负圈，可以将f0(e)初始化为0。如果图中也没有负权边的话，还可以直接利用Dijkstra算法计算h0。求得了fi和hi之后，通过沿着fi的残余网络中s到t的最短路增广，就得到了fi+1。只要在求得hi后，寻找一条只经过那些di(e)=0的边的s到t的路径，就可以轻松办到。为了求hi+1，我们需要求fi+1的残余网络上的最短路。利用势hi，这可以通过Dijkstra算法办到：
考虑fi+1的残余网络中的边e=(u,v)。如果e也是fi的残余网络中的边的话，那么根据h的定义有di(e)≥0。如果e不是fi的残余网络中的边的话，那么rev(e)一定是fi的残余网络中s到t的最短路中的边，所以有di(e)=-di(rev(e))=0。综上，fi+1的残余网络中的所有边e满足di(e)≥0，因而可以用Dijkstra算法求最短路。
如上所述，只要依次更新fi和hi，我们就能够在O(F|E|log|V|)或是O(F|V|2)的时间内求出最小费用流。
1 #include <cstdio> 2 #include <utility> 3 #include <vector> 4 #include <algorithm> 5 #include <queue> 6 #define number s-'0' 7 8 using namespace std; 9 10 typedef pair<int, int> P; 11 struct edge 12 { 13 int to; 14 int cap; 15 int cost; 16 int rev; 17 }; 18 19 const int INF=0x3f3f3f3f; 20 const int MAX_V=10000; 21 int V; 22 vector<edge> G[MAX_V]; 23 int h[MAX_V]; 24 int dist[MAX_V]; 25 int prevv[MAX_V], preve[MAX_V]; 26 27 int min(int x, int y) 28 { 29 if (x<y) return x; 30 return y; 31 } 32 33 void add_edge(int from, int to, int cap, int cost) 34 { 35 edge e; 36 e.to=to;e.cap=cap;e.cost=cost;e.rev=G[to].size(); 37 G[from].push_back(e); 38 e.to=from;e.cap=0;e.cost=-cost;e.rev=G[from].size()-1; 39 G[to].push_back(e); 40 } 41 42 int min_cost_flow(int s, int t, int f) 43 { 44 int res=0; 45 fill(h, h+V, 0); 46 while (f>0) 47 { 48 priority_queue<P, vector<P>, greater<P> > que; 49 fill(dist, dist+V, INF); 50 dist[s]=0; 51 que.push(P(0,s)); 52 while (!que.empty()) 53 { 54 P p=que.top();que.pop(); 55 int v=p.second; 56 if (dist[v]<p.first) continue; 57 for (int i=0; i<G[v].size(); i++) 58 { 59 edge &e=G[v][i]; 60 if (e.cap>0 && dist[e.to]>dist[v]+e.cost+h[v]-h[e.to]) 61 { 62 dist[e.to]=dist[v]+e.cost+h[v]-h[e.to]; 63 prevv[e.to]=v; 64 preve[e.to]=i; 65 que.push(P(dist[e.to], e.to)); 66 } 67 } 68 } 69 if (dist[t]==INF) 70 { 71 return -1; 72 } 73 for (int v=0; v<V; v++) h[v]+=dist[v]; 74 int d=f; 75 for (int v=t; v!=s; v=prevv[v]) 76 { 77 d=min(d, G[prevv[v]][preve[v]].cap); 78 } 79 f-=d; 80 res+=d*h[t]; 81 for (int v=t; v!=s; v=prevv[v]) 82 { 83 edge &e=G[prevv[v]][preve[v]]; 84 e.cap-=d; 85 G[v][e.rev].cap+=d; 86 } 87 } 88 }
关于顶点势h[i]的更新：
对于一条s→i的路，dist[i]=∑(e.cost)+h[s]-h[i]，而h[s]=0，所以dist[i]=∑(e.cost)-h[i]，而h[i]记录的是s到i的费用最短路，就是式子里的∑(e.cost)，所以h'[i]=dist[i]+h[i]，所以h[i]+=dist[i]。