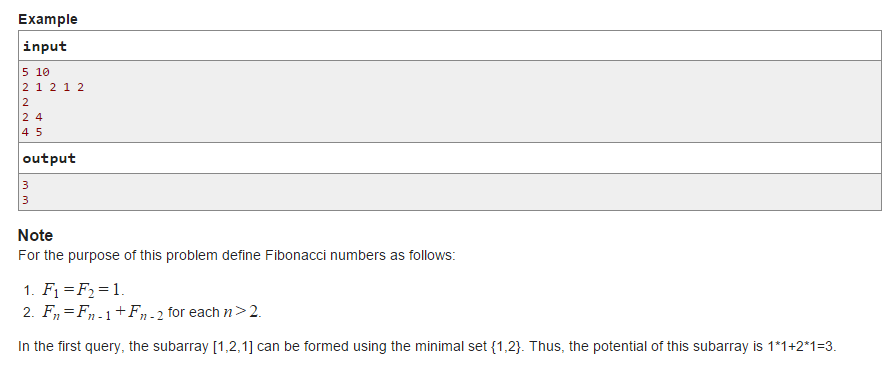
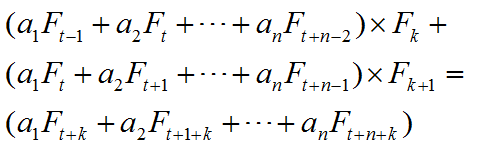题意: 给定一个长度最大为3万的序列,和最多3万个询问,每个询问问某区间[L,R]里的数,去掉重复然后排序之后,依次乘上斐波那契数列然后求和,结果对m取余的值。
区间优化用Mo's Algorithm(莫队算法),莫队算法的Add和Remove中使用线段树,所以整体复杂度是O(n*sqrt(n)*log2(n)).
这题一路TLE,从TLE26到TLE27到TLE29到TLE35都快绝望了,每次想尽办法优化都还是TLE,最后卡在TLE35,然后去翻了出题人的示例代码。
那个线段树居然是从0开始的,而且结构也很诡异,勉强看懂了,然后发现了我的两个线段树的访问可以合并成一个,于是优化了一下就过了,终于AC。
首先是莫队算法,简单来说就是,首先取p = sqrt(n),然后对于每个区间,先根据L/p再根据R排序。
然后定义变量L,R代表区间[L,R], 一步一步移动边界,使得[L,R]依次等于每个区间,每次移动边界都维护区间的答案,然后与每个询问的边界相等时记录答案。
最后一次输出答案即可。
由于区间的答案与区间内的数的顺序无关,也与数量无关,可以看做一个集合。
每次移动边界,就相当于从这个集合中加入或删除一个数,同时使用数据结构维护这个集合对应的值就行了。
莫队算法保证边界的移动次数为O((n sqrt(n)),每次移动边界需要用到线段树来维护答案O(log2(n)),所以总复杂度O(n*sqrt(n)*log2(n)).
所以,问题在于,如何实现莫队算法的Add和Remove函数。
首先要离散化,然后对每个数进行计数,只有数量从0到1或者从1到0时才真正进行集合的加入删除操作,所以下面的讨论中忽略重复值。
假设往集合中加入一个数v,那么整体的价值增加v * F[k],其中k是小于等于v的数的个数,然后所以比v大的数,所乘的斐波那契数的下标要+1.
把下标改变的过程叫做Shift。由上面的分析可以看出,加入v的时候,首先要知道v在集合中的排名,然后将v自己加入进去,然后比v大的所有值都Shift(1).
这也就是我最开始的思路,一个Add内访问3次线段树:
1.非递归线段树--------------维护v的排名
2.递归线段树-点修改-------加入v
3.递归线段树-区间修改----比v大的数全都Shift(1)
要这么做,就必须解决一个最大的问题:如何维护懒惰标记。
也就是说,在知道a[1]*F[1]+a[2]*F[2]+...+a[n]*F[n]的情况下,如何快速进行Shift(k),即得到a[1]*F[1+k]+a[2]*F[2+k]+...+a[n]*F[n+k]。
这就要用到一个神奇的公式: F[i-1]*F[k]+F[i]*F[k+1]=F[i+k]
有了这个,可以推出这个公式:
也就是说,只要维护相邻的两个F的版本,就可以O(1)进行Shift(k)操作,这也就保证了线段树的区间修改复杂度为O(log2(n))。
在代码中,VL代表第一行的括号,V代表第二行的括号,Shift(k)之后的V就是第三行括号,要将V Shift(k),就直接用上面的公式就行了。
再回到原来的方案,一个Add内访问3次线段树:
1.非递归线段树--------------维护v的排名
2.递归线段树-点修改-------加入v
3.递归线段树-区间修改----比v大的数全都Shift(1)
第一个发现可以优化的地方就是第一步可以省略,因为线段树维护了一个值S,表示每个节点的Shift值,比v小的有多少个数,v上的shift值就刚好是多少。
所以v对应的值是v*F[shift+1],所以点修改的时候记得下推Shift标记,到达叶节点时可以根据shift值来判断v的排名,可以省去第一步的非递归线段树。
除此之外就是各种小优化了,一路优化到了TLE35,然后去看题解给的代码,发现它是树状数组维护名次+线段树点修改就没了……
看到这里我就纳闷了,说好的区间修改呢……怎么就没了。正要把我习惯的线段树结构改成它那种结构的时候,突然想通了它的做法。
点修改的时候,在到达叶子之前,每次要选择向左走还是向右走,如果向左,就给右子树加上Shift(1)标记,如果向右走就跟原来一样。
这样,在点修改的同时解决了区间修改的打标记。
至此,一个Add内只需要访问一次线段树,Remove函数同上。
再有,由于有加入有删除,所以Shift的方向有正有负,对应到公式中,k值有正有负,所以对于负的斐波那契数列也需要求出来。
于是我加了个偏移量,下标正负3万的斐波那契数值全部都算了出来,反正k值为负公式照样成立,
标程里是直接求了负的斐波那契数列,然后需要正的的时候就求个绝对值。
---------------------------------------------------------------------------- 补充 --------------------------------------------------------------------------------
看了这篇文章: http://www.cnblogs.com/qscqesze/p/5224619.html ,发现这题居然可以暴力直接做。
思路极其简单粗暴,先将数组排序,然后从小到大依次考虑每个元素,对于每个元素,依次考虑这个元素是否在每个询问内,在就更新答案。
这样做的好处是,从询问的角度来看,就是将属于询问区间的所有元素从小到大给找了出来,省去了上面复杂的Shift操作,连负的斐波那契数列都用不到。
另一个好处就是代码超级短。虽然复杂度是O(n*q),但是由于常数特别小,也过了。
莫队(3541ms 2592KB)
暴力(4461ms 900KB)
最后附上代码:
/*
莫队算法 3541 ms 2592 KB
*/
#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
#define out(i) <<#i<<"="<<(i)<<" "
#define OUT1(a1) cout out(a1) <<endl
#define OUT2(a1,a2) cout out(a1) out(a2) <<endl
#define OUT3(a1,a2,a3) cout out(a1) out(a2) out(a3)<<endl
#define maxn 30001
using namespace std;
//题目数据
int n,m,q;
int A[maxn],RankA[maxn];
//MO's Algorithm
int ANS[maxn],p;
struct LR{
int L,R,id;
bool operator<(const LR &B)const{
return L/p < B.L/p || L/p == B.L/p && R < B.R;
}
}I[maxn];
int Count[maxn];
//斐波那契数列
int Fibs[maxn<<1];
//离散化
int Rank[maxn],Rn;
//线段树--区间修改 S:shift值,V:当前值, VL:Shift(-1)的值
int S[maxn<<2],VL[maxn<<2],V[maxn<<2];
//离散化
void SetRank(){
sort(Rank+1,Rank+Rn+1);
int I=1;
for(int i=2;i<=Rn;++i)
if(Rank[i]!=Rank[i-1])
Rank[++I]=Rank[i];
Rn=I;
}
int GetRank(int x){
int L=1,R=Rn,M;//[L,R] first >= x
while(L^R){
M = (L+R)>>1;
if(Rank[M] < x) L=M+1;
else R = M;
}
return L;
}
//斐波那契数列
void GetFibs(){
Fibs[Rn]=0;
Fibs[Rn+1]=1;
for(int i=2;i<=Rn;++i) Fibs[Rn+i]=(Fibs[Rn+i-1]+Fibs[Rn+i-2])%m;
for(int i=1;i<=Rn;++i) Fibs[Rn-i]=(Fibs[Rn-i+2]-Fibs[Rn-i+1]+m)%m;
}
//线段树--(带标记的点修改)
void Clear(){//初始化线段树--全零
memset(S,0,sizeof(S));
memset(VL,0,sizeof(VL));
memset(V,0,sizeof(V));
}
void PushUp(int rt){//更新信息
V[rt]=(V[rt<<1]+V[rt<<1|1])%m;
VL[rt]=(VL[rt<<1]+VL[rt<<1|1])%m;
}
void Shift(int rt,int shift){//节点值右移shift位
int NV,NVL;
NV =(VL[rt]*Fibs[Rn+shift]+V[rt]*Fibs[Rn+shift+1])%m;
NVL =(VL[rt]*Fibs[Rn+shift-1]+V[rt]*Fibs[Rn+shift])%m;
V[rt]=NV;VL[rt]=NVL;
}
void PushDown(int rt){//下推标记
if(S[rt]){
S[rt<<1]+=S[rt];
S[rt<<1|1]+=S[rt];
Shift(rt<<1,S[rt]);
Shift(rt<<1|1,S[rt]);
S[rt]=0;
}
}
void Add(int X,int l,int r,int rt){//增加点
if(l==r){
VL[rt]=Rank[l]%m*Fibs[Rn+S[rt]]%m;
V[rt]=Rank[l]%m*Fibs[Rn+S[rt]+1]%m;
return;
}
int m=(l+r)>>1;
PushDown(rt);
if(X <= m) {
Add(X,l,m,rt<<1);
S[rt<<1|1]++;
Shift(rt<<1|1,1);
}
else Add(X,m+1,r,rt<<1|1);
PushUp(rt);
}
void Remove(int X,int l,int r,int rt){//减少点
if(l==r){
V[rt]=VL[rt]=0;
return;
}
int m=(l+r)>>1;
PushDown(rt);
if(X <= m) {
Remove(X,l,m,rt<<1);
S[rt<<1|1]--;
Shift(rt<<1|1,-1);
}
else Remove(X,m+1,r,rt<<1|1);
PushUp(rt);
}
//Mo's Algorithm
void Mo_Init(){
memset(Count,0,sizeof(Count));
Clear();
//预处理每个值的离散之后的下标
for(int i=1;i<=n;++i) RankA[i]=GetRank(A[i]);
}
void Mo_Add(int k){
if(!Count[k]++) Add(k,1,Rn,1);
}
void Mo_Remove(int k){
if(!--Count[k]) Remove(k,1,Rn,1);
}
int main(void)
{
while(~scanf("%d%d",&n,&m)){
Rn=0;
for(int i=1;i<=n;++i) {
scanf("%d",&A[i]);
Rank[++Rn]=A[i];
}
SetRank();//离散化
scanf("%d",&q);
for(int i=1;i<=q;++i) scanf("%d%d",&I[I[i].id=i].L,&I[i].R);
p = sqrt(n);
sort(I+1,I+q+1);//区间排序
GetFibs();//初始化Fibs数组
Mo_Init();//各种初始化
//开始莫队算法
int L=1,R=0;
for(int i=1;i<=q;++i){
//移动边界
while(R > I[i].R) Mo_Remove(RankA[R--]);
while(R < I[i].R) Mo_Add(RankA[++R]);
while(L < I[i].L) Mo_Remove(RankA[L++]);
while(L > I[i].L) Mo_Add(RankA[--L]);
//记录答案
ANS[I[i].id]=V[1];
}
//输出答案
for(int i=1;i<=q;++i){
printf("%d\n",ANS[i]);
}
}
return 0;
}
/* 暴力(4461ms 900KB)*/
#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
#define out(i) <<#i<<"="<<(i)<<" "
#define OUT1(a1) cout out(a1) <<endl
#define OUT2(a1,a2) cout out(a1) out(a2) <<endl
#define OUT3(a1,a2,a3) cout out(a1) out(a2) out(a3)<<endl
#define maxn 30001
using namespace std;
//题目数据
int n,m,q;
struct T{
int A,id;
bool operator <(const T &B)const{return A < B.A;}
}I[maxn];
int Fibs[maxn];
int ANS[maxn];
int Step[maxn];
int Last[maxn];
int L[maxn],R[maxn];
int main(void)
{
while(~scanf("%d%d",&n,&m)){
for(int i=1;i<=n;++i)
scanf("%d",&I[I[i].id=i].A);
sort(I+1,I+n+1);
scanf("%d",&q);
for(int i=1;i<=q;++i)
scanf("%d%d",&L[i],&R[i]),ANS[i]=Step[i]=Last[i]=0;;
Fibs[0]=0;Fibs[1]=1;
for(int i=2;i<=n;++i) Fibs[i]=(Fibs[i-1]+Fibs[i-2])%m;
for(int i=1;i<=n;++i){
for(int j=1;j<=q;++j){
if(I[i].id < L[j] || I[i].id > R[j] || I[i].A == Last[j]) continue;
ANS[j]=(ANS[j]+(Last[j]=I[i].A)%m*Fibs[++Step[j]])%m;
}
}
for(int i=1;i<=q;++i) printf("%d\n",ANS[i]);
}
return 0;
}