题目链接:https://www.jisuanke.com/contest/1409?view=challenges
A题
题意:给你n个硬币,m次操作,每次抛上去k个硬币,问你m次操作后硬币向上的次数的期望。
思路:当有至少 k 枚硬币面朝下时,则选 k 枚面朝下的硬币去抛掷(任意k 枚都可以);如果不足 k 枚面朝下,则在选择所有面朝下的硬币的基础上再额外选择若干面朝上的银币。
dp[i][j] 是第i次j个向上的概率。代码有注释,详情看代码。
#include<bits/stdc++.h>
#define ll long long
using namespace std;
double dp[105][105];
double C[105][105];
double fac[105];
void init()//预处理组合数
{
C[0][0]=1;
for(int i=1;i<105;i++)
for(int j=0;j<=i;j++)
C[i][j]=(j == 0) ? 1:(C[i-1][j]+C[i-1][j-1]);
fac[0] = 1;
for(int i = 1;i <= 100;i++) //预处理次数
fac[i] = fac[i-1]*0.5;
}
int main()
{
init();
int t,n,m,i,j,k,x;
scanf("%d",&t);
while(t--)
{
scanf("%d%d%d",&n,&m,&x);
memset(dp,0,sizeof(dp));
dp[0][0] = 1.0;
for(i = 0;i < m;i++)//m次
{
for(j = 0;j <= n;j++)//j个朝上的
{
for(k = 0;k <= x;k++)//抛上去的k个中有多少个下来是正面的
{
if(n - j >= x) //都从朝下的里面选k个朝上
dp[i+1][j+k] += dp[i][j]*C[x][k]*fac[x];
else //需要从在上的里面选
dp[i+1][k+n-x] += dp[i][j]*C[x][k]*fac[x];
}//dp[i][j] 抛掷i次j个朝上的概率
}
}
double ans = 0;
for(i = 0;i <= n;i++)//期望
ans = ans + dp[m][i]*i;
printf("%.3f\n",ans);
}
return 0;
}B题
题意:给你4个数求一个max(a*b-c*d)
思路:sort一下就行。
D题
题意:给你个圆和k个点,问你最多分割多少块。
思路:结论题,蓝书123页。
G 题
题意:给你n个点,构成一个山峰的形状,保证第一个点事原点,保证最后一个点一定落在X轴。
思路:套一下求多边形面积公式即可。自己也可以百度下。
I题
题意:给你一棵树,然后给你问你树上两点(通过唯一的路可达)之间是否可以异或成他给的那个值,两点之间的边权随意设定。给你c个条件,问你前多少个条件一定可以满足。
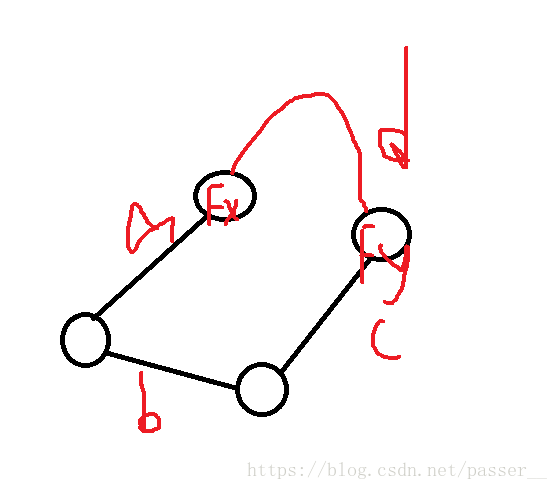
思想:用带权并查集解决这一类问题,对于一些莫名的路径,先用并查集将连续的区间连接起来,如果查询的区间属于一个大的联通块的话,只需要查询下他们到共同的一个节点的sum1^sum2是否等于他们需要的valu,因为共同的异或之后就是0了,所以的到的就是之间的值,对于是2个联通块的话,需要将2个连接成一个,将他们2个公共点相连,而且知道他们之间的值,便可以知道另外一条边的值,如下图。
对于已知a,b,c的话,那么d来说就等于,a^b^c。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int fa[100005];
ll valu[100005];
int find(int x)
{
if(x==fa[x])
return x;
int fx=fa[x];
fa[x]=find(fa[x]);
valu[x]^=valu[fx]; //从底到上的反过来
return fa[x];
}
int check(int x,int y,ll val)
{
int fx=find(x);
int fy=find(y);
if(fx==fy)
return 0;
valu[fx]^=valu[x]^valu[y]^val; //如果异或的部分
fa[fx]=fy;
return 1;
}
int main()
{
int t;
scanf("%d",&t);
while(t--)
{
int n,c,u,v;
ll Valu;
scanf("%d%d",&n,&c);
for(int i=0;i<n-1;i++)
scanf("%d%d",&u,&v);
for(int i=1;i<=n;i++)
{
fa[i]=i;
valu[i]=0;
}
int ans=c;
for(int i=0;i<c;i++)
{
scanf("%d%d%lld",&u,&v,&Valu);
if(flag && check(u,v,Valu)==0 && (valu[u]^valu[v])!=Valu)//同一个区间而且不等
ans=i;
}
printf("%d\n",ans);
}
return 0;
} K题
题意:给你个T表的规则,就是对于1 ≤ r and 1 ≤ c ≤ r. 如果gcd(r,c)== 1, Tr,c = c, 否则等于0。S表就是对于某一行来说求当前点到最后的一个对于T表的后缀和。然后给你个K求出来K行的一个S表的和。
官方题解:

因为对于每个点他只能贡献他的位置的次数,比如5 他会给1 2 3 4 5 这五个位置贡献,所以就是5*5 就是5^2
然后考虑删去那些等于0的位置产生的贡献,这些位置肯定是K的素因子和它这些因子的倍数。对于1e8来说,最多不会超过9个素因子,因此枚举这些因子产生的子集即可,枚举子集时间复杂度最大是2^9。剩下就是容斥原理的东西了,对于1^2+2^2+-----k^2,有一个公式可以计算(1/6)n(n+1)(2n+1) 推导过程:https://zhidao.baidu.com/question/87353666.html
对于某个素因子的倍数来说,提取这个素因子*素因子,例如10 2的话就是2^2+4^2+6^2+8^2 提取2^2(1^2+2^2+3^2+4^2)同样可以用那个公式。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 1e5+10;
const ll mod = 998244353;
int yin[maxn];
ll inv(ll b){return b==1?1:(mod-mod/b)*inv(mod%b)%mod;}
ll Cal(ll x,ll n)
{
ll k=(n-x)/x+1;//计算除去当前有多少 提取x^2 之后是(1^2+2^2----)
return k*(k+1)%mod*(2*k%mod+1)%mod*inv(6)%mod*x%mod*x%mod;
}
int main()
{
ll t,k;
scanf("%d",&t);
while(t--)
{
scanf("%d",&k);
ll n=k;
int top=0;
for(int i=2;i*i<=k;i++)//求因子
{
if(k%i==0)
{
yin[top++]=i;
while(k%i==0)
k=k/i;
}
}
if(k>1)
yin[top++]=k;
ll ans=0;
for(int i=1;i<(1<<top);i++)
{
int Sum=0;
int Ans=1;
for(int j=0;j<top;j++)//枚举素因子
{
if((1<<j)&i)//枚举子集
{
Sum++;//控制加还是减
Ans=Ans*yin[j];//计算从哪个数开始
}
}
ll temp=Cal(Ans,n);
if(Sum&1)//奇数
ans=(ans+temp)%mod;
else
ans=(ans-temp+mod)%mod;
}
ans=(Cal(1,n)-ans+mod)%mod;//1^2+2^2+3^2------(n-1)^2
printf("%lld\n",ans);
}
return 0;
}