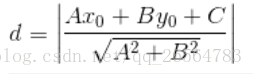统计学习笔记之感知机

一、感知机模型

感知机顾名思义，感知输入作出判断的一个模型，实际是一个二分类线性分类器，即判别模型。感知机实际实现方式就是对于任何输入空间（特征空间）中将实例划分成正负两类的超平面。所谓超平面，就是在N维空间中的一个平面，这个N很多时候远大于我们可见的三维及以下的具象空间。

感知机模型

输入空间 $\mathbb{X} \in R^{n}$ ,输出空间 $\mathbb{Y}=\left \{ -1,+1 \right \}$ .由输入到输出的映射函数如下：

$f\left ( x \right )=sign(w\cdot x+b)$

这样形势的模型被称之为感知机。其中 $w\in R^{n}$ 即权值， $b\in R^{n}$ 即偏置值。其中，

$sign(x)=\left\{\begin{matrix} +1, x\geqslant 0 & \\ -1, x< 0 \end{matrix}\right.$

显然， $w\cdot x+b=0$ 是一个线性方程，当对应到N维空间中，当是一个超平面的表达式。其中， $w$ 是法向量， $b$ 是超平面截距。而这个超平面将该多维空间划分成两部分，位于这两部分的点（特征向量）即可对应我们的正负二分类。具象到二维空间，我们可以得到如图一所示，高维空间可类推之。

图一

那么对应到工程上，我们通常遇到的问题是对于已知数据集 $T=\left \{ (x_{1},y_{1}),(x_{2},y_{2})\cdots (x_{n},y_{n}) \right \}$ ，其中 $x_{i}\in \mathbb{X}=R^{n},y_{i}\in \mathbb{Y}=\left \{ -1,+1 \right \}, i=1,2\cdots N$ ,如果我们能找到相应的参数确定存在这个超平面，使得对于所有 $y_{i}=+1$ 都满足 $w\cdot x+b>0$ ，同理在 $y_{i}=-1$ 时，都有 $w\cdot x+b<0$ ，因此这种情况也称为线性可分。当然这样的超平面可能不存在，那么我们称该数据集为线性不可分。

二、学习策略

接下来为了找到这个超平面，我们需要确定一个学习策略，即定义损失函数并将损失函数极小化。考虑到连续可导(便于梯度下降），我们考虑选用的损失函数是误分类点到超平面的总距离，即

$\frac{1}{\left \| w \right \|}\left | w\cdot x_{0}+b \right |$

其中， $\left \| w \right \|$ 为 $w$ 的 $L_{2}$ 范数。显然这就是点到直线的距离公式，不同的这是高维的表达形式，没明白可仔细对照之：

不难得出对于误分类的点有：

$-y_{i}\left ( w\cdot x_{i}+b \right )>0$

因此误分类点到超平面的距离有：

$-\frac{1}{\left \| w \right \|}y_{i}\left ( w\cdot x_{i}+b \right )$

假设被超平面S误分类的点集合是M, 那么所有误分类点到超平面S的总距离为：

$-\frac{1}{\left \| w \right \|}\sum_{x_{i}\in M}^{ } y_{i}\left ( w\cdot x_{i}+b \right )$

忽略 $\frac{1}{\left \| w \right \|}$ ，即损失函数

$L\left ( w,b \right ) = -\sum_{x_{i}\in M}^{ } y_{i}\left ( w\cdot x_{i}+b \right )$

这也被称为样本点的函数间隔。显然，损失函数值域非负，当误分类点数为0，损失函数值也为0，当误分类点越少或误分类点离超平面越近，损失函数的值都越小。在误分类时，该损失函数是参数 $w,b$ 的线性函数，而正确分类时恒为0，因此该函数是 $w,b$ 线性可导函数。

因此，问题便转化为求损失函数在相应给定的数据集上的损失最小的参数w,b。

$min_{w,b}L\left ( w,b \right )=-\sum_{x_{i}\in M}^{ } y_{i}\left ( w\cdot x_{i}+b \right )$

具体采用随机梯度下降算法。首先，任意选取一个超平面，对应参数 $w_{0},b_{0}$ ，然后不断用梯度下降不断使得目标函数极小化。所谓的随机梯度下降是指：极小化过程并不是一次就使全部误分类点的梯度下降，而是随机选取一个误分类点使其梯度下降。

易得，损失函数梯度：

$\triangledown _{w}L\left ( w,b \right ) = -\sum_{x_{i}\in M}^{ }y_{i}x_{i}$ , $\triangledown _{b}L\left ( w,b \right ) = -\sum_{x_{i}\in M}^{ }y_{i}$

随机选取一个误分类点更新参数：

$w\leftarrow w+\eta y_{i}x_{i}$ , $b\leftarrow b+\eta y_{i}$ ( $\eta$ 步长，即学习率)

通过迭代，使得损失函数不断减小，直至为0。这里可以参考一道例题帮助理解。值得一提的是这个过程得到的解不一定是唯一的，随机梯度下降过程选择的点不同，最后解得的超平面可以是不同的。

三、算法收敛性

可以证明算法是收敛的，即通过有限步计算可求得最终得损失降到最小，从而确定相应得参数。相关证明可见相关资料，不再赘述。需要注意该证明过程隐含了数据线性可分得条件，当数据线性不可分时，感知机学习算法不收敛，迭代结果震荡。