T1:潜伏者
考察知识:map,模拟
算法难度:XX 实现难度:XX
分析:我们开一个map<char,char>mp
用mp[a]=b表示明文b为密文a的映射
我们只需要输入后一个一个的映射,然后判断是否合理就可以了
但是判断是否合理要考虑严谨,这里比较容易丢分
细节见代码:
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<map>
using namespace std;
char str[3][105];
bool err,used[128];
int cnt=0;
map<char,char>mp;
int main(){
scanf("%s%s%s",str[0],str[1],str[2]);
for(int i=0;str[1][i]!='\0';i++)
if(!mp.count(str[0][i])&&!used[(int)str[1][i]])
used[(int)str[1][i]]=true,mp[str[0][i]]=str[1][i],cnt++;
else if(mp[str[0][i]]!=str[1][i])//如果同一密文的映射不一致
err=true;
if(err||cnt<26) printf("Failed");//注意:明文26个字母必须全部被映射
else{
for(int i=0;str[2][i]!='\0';i++) putchar(mp[str[2][i]]);
}
return 0;
}T2:Hankson 的趣味题
考察知识:数论,枚举
算法难度:XXX+ 实现难度:XX+
分析:显然,从1暴力枚举x肯定会超时
部分原题:
2. x 和 b0 的最小公倍数是 b1。
明白了吗,这里就是突破口,这句话说明x一定能整除b1(最小公倍数的基本知识)
所以我们枚举可以整除b1的数就可以了,枚举量为,这样就可以AC了
代码:
#include<cstdio>
int n,a,a1,b,b1;
int gcd(int a,int b){return b?gcd(b,a%b):a;}
int lcm(int a,int b){
long long T=(long long)a*b/gcd(a,b);
return (int)T;
}
void solve(){
int cnt=0,x_;
for(int x=1;x*x<=b1;x++) if(b1%x==0){
if(gcd(x,a)==a1&&lcm(x,b)==b1) cnt++;
if(x*x!=b1) {
x_=b1/x;
if(gcd(x_,a)==a1&&lcm(x_,b)==b1) cnt++;
}
}
printf("%d\n",cnt);
}
int main(){
scanf("%d",&n);
while(n--){
scanf("%d%d%d%d",&a,&a1,&b,&b1);
solve();
}
return 0;
}T3:最优贸易
考察知识:图论
算法难度:XXX ~ XXXX 实现难度:XXX ~ XXXX
分析:这道题方法比较多:
1.强连通分量缩点+DAG的动态规划(实现难度:XXXX)
我们可以先进行缩点,然后进行动态规划
我某次考试的时候做这道题用的这种方法,忘记记忆化了,TLE,60分
而且这种方法代码实现比较困难,涉及两个图论知识,就不解释了
2.spfa变形(实现难度:XXX)
a.我们先求出从起点(1点)到所有可以经过的点的每一个点的最小权值mx[i]
例:如图,6点的最小权值为1,因为有路径1->4->5->1,经过的5点权值最小,为1
b.然后我们再求出从终点(n点)到所有可以反向经过的点的每一个点的最大权值mn[i](注意:这里要反向建图)
例:还是上面的图,3点的最大权值为5,因为从5可以反向到3
c.枚举1到n的所有点,答案为每个点的最大权值减最小权值(mx[i]-mn[i])的最大值
对于a.b.的实现我们可以用类似于spfa的方法,这里就不详细讲解了
最后关于该方法正确性的证明:
我们考虑一条要经过点k的路线,则从1到k经过最小权值的点为mn[i],
然后从k到n,经过的最大权值点为mx[i],
所以要经过点k的最大收益为mx[i]-mn[i]
我们枚举经过k就可以得到经过所有点最大收益的最大收益
证毕
代码:
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<queue>
using namespace std;
const int maxn=100005;
struct edge{
int to,next;
}e[maxn*10],re[maxn*10];
int head[maxn],np,head_[maxn],np_;
void add(int u,int v){
e[++np]=(edge){v,head[u]};
head[u]=np;
re[++np_]=(edge){u,head_[v]};//反向建图
head_[v]=np_;
}
int n,m,p[maxn],mx[maxn],mn[maxn];
bool vis[maxn],inq[maxn];
void spfa_min(int s){
queue<int>q;
int i;
memset(inq,0,sizeof(inq));
mn[s]=p[s],vis[s]=inq[s]=true;
q.push(s);
while(!q.empty()){
i=q.front(),q.pop(),inq[i]=false;
for(int p_=head[i];p_;p_=e[p_].next){
int j=e[p_].to;
if(!vis[j]){
mn[j]=min(p[j],mn[i]);
q.push(j),inq[j]=vis[j]=true;
}else if(mn[i]<mn[j]){//类似于spfa
mn[j]=mn[i];
if(!inq[j]) inq[j]=true,q.push(j);
}
}
}
}
void spfa_max(int s){
queue<int>q;
int i;
memset(inq,0,sizeof(inq));
mx[s]=p[s],vis[s]=inq[s]=true;
q.push(s);
while(!q.empty()){
i=q.front(),q.pop(),inq[i]=false;
for(int p_=head_[i];p_;p_=re[p_].next){
int j=re[p_].to;
if(!vis[j]){
mx[j]=max(p[j],mx[i]);
q.push(j),inq[j]=vis[j]=true;
}else if(mx[i]>mx[j]){
mx[j]=mx[i];
if(!inq[j]) inq[j]=true,q.push(j);
}
}
}
}
void build(){
int x,y,z;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) scanf("%d",p+i);
for(int i=1;i<=m;i++){
scanf("%d%d%d",&x,&y,&z);
add(x,y);
if(z==2) add(y,x);
}
}
void solve(){
int ans=0;
memset(mn,0x7f,sizeof(mn));
spfa_min(1);
memset(vis,0,sizeof(vis));
spfa_max(n);
// for(int i=1;i<=n;i++) printf("mx[%d]=%d mn[%d]=%d\n",i,mx[i],i,mn[i]);
for(int i=1;i<=n;i++) ans=max(ans,mx[i]-mn[i]);
printf("%d\n",ans);
}
int main(){
build();
solve();
return 0;
}T4:靶形数独
考察知识:搜索+剪枝,搜索的优化,数独,舞蹈链
算法难度:XXXX 实现难度:XXX
分析:
这道题最优算法肯定是舞蹈链,但是我并不了解,就不介绍这种方法了
下面介绍搜索算法:
我们用sdk[9][9]表示这个数独(下标0~8),row[i][k]=true表示第i行(横着的)k数字已经使用,col[j][k]=true表示第j列(竖着的)的数字k已经使用,sq[i][j][k]=true表示坐标为(i,j)小九宫格中k已经使用(如图)
我们先读入数独,例如:我们读入了坐标为(i,j)的数k
那么:
sdk[i][j]=k,row[i][k]=col[j][k]=sq[i/3][j/3]=true;
现在明白下标0-8的好处了吗?
然后我们开始从坐标(0,0)向坐标(8,8)搜索,遇到没有填的空就枚举一个合适的值(要充分运用row,col,sq数组的限制作用),然后继续向下搜索
好,算法描述完毕,按上面的方法就可以的80分,还是不错吧
下面介绍优化方法:
我们不从(0,0)向(8,8)搜索,而该为一行一行的搜索,优先搜索某行i满足i行的填了的数字比其他行多,这样就可以AC了
为了让大家更加了解数独,我再加一个方法(人脑解数独基本方法,会玩数独的可以跳过):宫内行列排除法
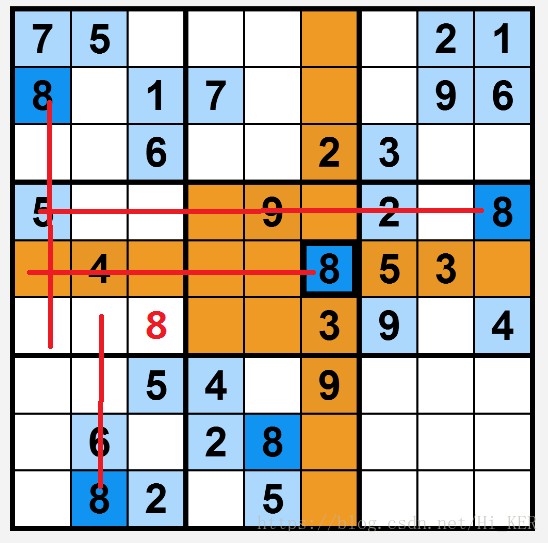
如图有红线的地方不能填8,而一个九宫格内必须要有一个8,所以我们在(5,2)处填8(红色)
明白了吗,这种方法就是根据其他九宫格的数,利用行列不能再填该数,加上目标九宫格的占位(已经有的数占位)来推一个数的
再举一例:
但是面对这道题,这种方法的优化不是很有用,提升速度有限,但是这确实是人脑解数独最基本最常用的方法
代码:
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
#define F(var,L,R) for(int var=L;var<=R;var++)
#define Max(var,var_) var=var>(var_)?var:(var_)
int P[9][9]={
{6,6,6,6,6,6,6,6,6},
{6,7,7,7,7,7,7,7,6},
{6,7,8,8,8,8,8,7,6},
{6,7,8,9,9,9,8,7,6},
{6,7,8,9,10,9,8,7,6},
{6,7,8,9,9,9,8,7,6},
{6,7,8,8,8,8,8,7,6},
{6,7,7,7,7,7,7,7,6},
{6,6,6,6,6,6,6,6,6}},sdk[9][9],ans=-1;
bool row[9][10],col[9][10],sq[3][3][10];
struct Q{int id,num;}q[9];
bool cmp(Q A,Q B){return A.num>B.num;}
int fill_blanks(int I,int J){
int cnt,flag=0,i_,j_;
F(i,0,2) F(j,0,2) F(k,1,9) if(!sq[i][j][k]){
cnt=0;
F(ii,i*3,i*3+2) F(jj,j*3,j*3+2)
if(!sdk[ii][jj]&&!(row[ii][k]||col[jj][k])) i_=ii,j_=jj,cnt++;
if(cnt==1) flag=1,row[i_][k]=col[j_][k]=sq[i][j][k]=true,sdk[i_][j_]=k;
}
return flag;
}
void dfs(int i__,int j,int sum){
if(i__>8){Max(ans,sum);return;}
int i=q[i__].id;
int i_=(j==8)?i__+1:i__,j_=(j==8)?0:j+1;
if(sdk[i][j]) dfs(i_,j_,sum+sdk[i][j]*P[i][j]);
else{
F(k,1,9) if(!(row[i][k]||col[j][k]||sq[i/3][j/3][k])){
row[i][k]=col[j][k]=sq[i/3][j/3][k]=true,sdk[i][j]=k;
dfs(i_,j_,sum+k*P[i][j]);
row[i][k]=col[j][k]=sq[i/3][j/3][k]=false,sdk[i][j]=0;
}
}
}
int main(){
int k;
F(i,0,8) F(j,0,8){
scanf("%d",&k);
row[i][k]=col[j][k]=sq[i/3][j/3][k]=true,sdk[i][j]=k;
}
while(fill_blanks(0,0));//宫内行列排除法
F(i,0,8){
int cnt=0;
F(j,0,8) if(sdk[i][j]) cnt++;
q[i].id=i,q[i].num=cnt;
}
sort(q,q+9,cmp);
dfs(0,0,0);
printf("%d\n",ans);
return 0;
}