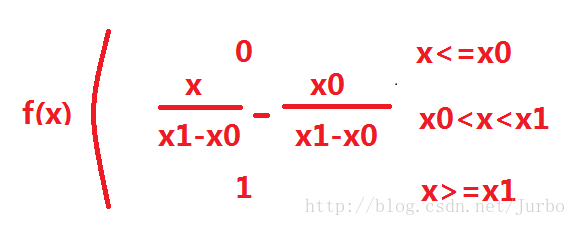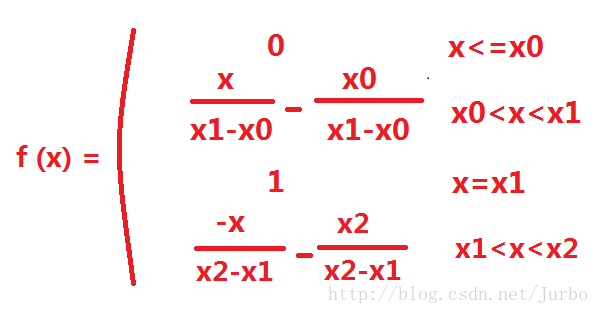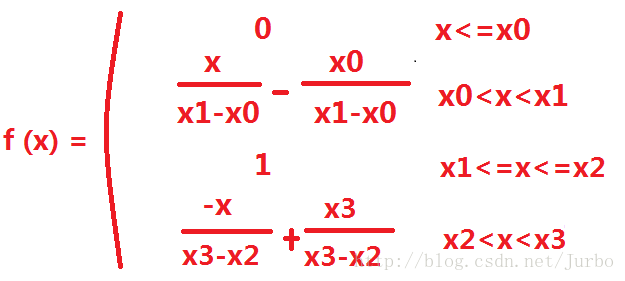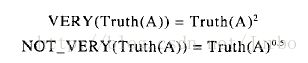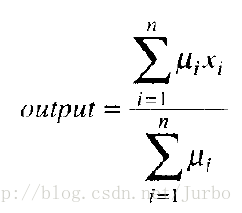游戏开发中的人工智能（十）：模糊逻辑

版权声明：本文为Jurbo原创文章，转载请加上链接和作者名，标明出处。 https://blog.csdn.net/Jurbo/article/details/75949360

接上文 游戏开发中的人工智能（九）：有限状态机

本文内容：开发人员经常把模糊逻辑和有限状态机结合起来使用，甚至取代有限状态机。本章将会学到模糊逻辑为什么优于传统的逻辑技术。

---

模糊逻辑

在生活中，我们经常会用“有一点”“差不多”“几乎没有”“接近于”这样的描述词，会模糊边界。

在传统逻辑中，非黑即白，就是0或者1，不是0，就是1，不存在其他的情况。而模糊逻辑，可以存在0到1之间的其他情况即灰色地带。比如高矮胖瘦，到底多高才叫高，多矮才叫矮，没有一个明显的界限，可以说有点高，很高，非常高，所以边界（或者说临界条件）是模糊的。0到1之间数值的大小，代表该事件属于0或者1的程度的大小即隶属度。我们可以编写隶属函数来判断隶属度，或者说概率来表示这个状态。隶属度表示程度，它的值越大，表明这个状态的概率越高，反之则表明这个状态的概率越低 。

1965 年，加州柏克莱大学教授 Lotfi Zadeh 写了第一篇论述模糊集合理论的论文。

模糊逻辑的两项基本原则是：

1. 模糊逻辑的含义：让计算机以一种接近人类行为的方式解决问题
2. 模糊逻辑的本质：一切都和程度有关

在游戏中使用模糊逻辑

在游戏中可以以各种方式使用模糊逻辑。这里只介绍三个方面，控制、威胁评估、分类。

你可以用模糊逻辑控制队友或其他非玩家角色，也可以用模糊逻辑评估玩家展示的威胁，也可以用模糊罗去区分玩家和非玩家角色。

控制

模糊逻辑可以控制游戏中的单位的运动，使其平滑地通过拐点并绕开障碍物。（利用隶属函数控制物体的转向力）

威胁评估

模糊逻辑在游戏中的另一个可能的应用牵涉到决策，不再是直接的运动控制。

在战争仿真游戏中，计算机军队时常得配置防卫军队，以抵抗潜在威胁的敌军。假设计算机军队知道敌军军队的距离和敌军的规模。距离可以用附近、逼近、远和很远来表示，而规模可以用零星、少量、中等、大型或巨型来表示。

扫描二维码关注公众号，回复： 2952126 查看本文章

有了这些信息，我们就可以用模糊逻辑来让计算机评估敌军带来的威胁。威胁的成都可以视为无、低等、中等或高等，确认威胁成都之后，计算机就能依次决定并用适当的兵力部署防卫。

分类

假设你想将游戏中的玩家角色和非玩家角色，依照他们的战斗能力予以区分等级。你可以在等级的基础上，还参考玩家角色的体力、被击中的次数、武器熟练度、盔甲等级。最后，你会结合这些因素，做出等级分类，诸如弱不禁风、不费力、平庸、顽强、可怕等。

例如，如果玩家被击中的次数高、盔甲等级普通、体力好、武器熟练度低，等级也许就是平庸。模糊逻辑可以让你决定这种等级。

模糊逻辑基础

概论

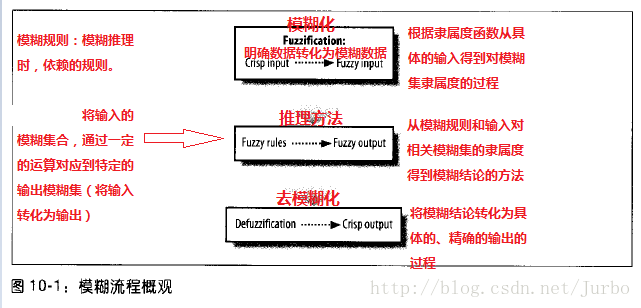
模糊流程由三个基本步骤组成，如图10-1：

模糊流程由三个基本步骤组成，分别是：

1. 模糊化：根据隶属度函数从具体的输入得到对模糊集隶属度的过程
2. 推理方法：从模糊规则和输入对相关模糊集的隶属度得到模糊结论的方法
3. 去模糊化：将模糊结论转化为具体的、精确的输出的过程

计算流程大致如下：

输入（采集明确数据） ——> 模糊化（根据隶属度函数，如分段函数、分布函数，再从具体的输入，得到 隶属度模糊集合（特征数据）） ——> 模糊规则库 + 推理方法 ——> 模糊结论——> 去模糊化

模糊化

模糊系统的输入是明确的数字。在模糊化的过程中，我们要将这些明确的值，根据隶属函数，对应到模糊集中的隶属度。

隶属函数

隶属函数（或译为归属函数），就是把输入变量对应到模糊集合中某个介于0和1之间的值，求出隶属度。如果在给定集合中的隶属度是1，我们就说该输入数据对集合而言是绝对真。如果隶属度是0，则我们说对该集合而言为绝对假。如果隶属度介于0和1之间，则为某种范围的真，即某种程度为真。（例：有点高，即某种程度的高）

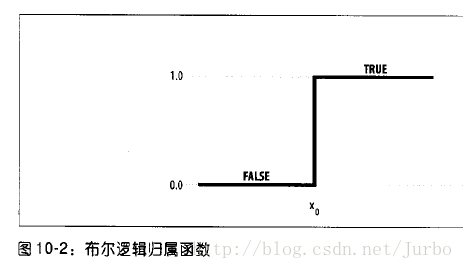
探讨模糊逻辑的隶属函数之前，我们先谈传统逻辑比如说布尔逻辑的隶属函数。图10-2 所示的就是布尔逻辑的隶属函数（归属函数）。

观察 图10-2 可知，当输入数据小于 x0 时，则结果取假（false），而当输入数据大于 x0 时，结果取真（true）。没有中间值，即传统逻辑中的非黑即白，非零即1，非假即真。举个例子，假如 x0=170 斤，则任何人超过 170 斤 就是超重，低于 170 斤 的就是不超重，即使某人 169 斤，仍然被视为不超重。这对现实生活中的判断而言很不合理，但是如果模糊隶属函数，则可以让我们实现从 false 到 true 或者说从不超重到超重之间的逐渐转移。

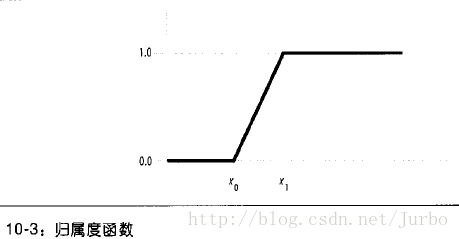
图10-3 是模糊逻辑的隶属函数图。如下所示。

从图10-3 中可以看出，0到1之间的逐渐变化。小于 x0 时，则结果取假（false）即隶属度为0，而大于 x1 的值，结果取真（true）即隶属度为1。介于 x0 到 x1 之间的值，隶属度则呈线性变化。

使用直线的点斜式方程，可以写出表示此隶属度函数的方程式，如下所示。

回到体重例子。让该函数代表超重隶属。令 x0 等于175，而 x1 等于 195。如果某人重175斤，根据该隶属函数，他的隶属程度为0，也就是不超重。如果他重185 斤，则根据计算，他的隶属度为 0.5，也就是有点超重。

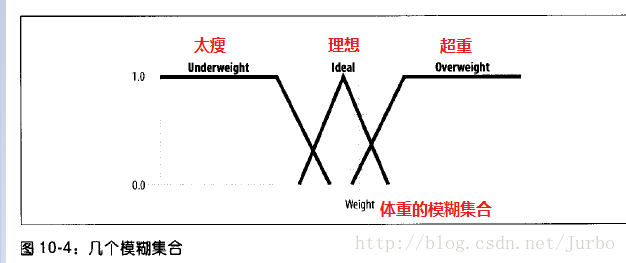
一般而言，我们关注的是输入变量根据隶属函数，对应到模糊集合中的程度。例如，我们想知道某人的体重是超重、太瘦、或者理想。就此而言，我们要设立模糊集合，这样我们才能根据隶属函数，观察它的隶属度是落在哪个区间的，即代表的是什么程度。模糊集合如图10-4 所示。

有了这样的集合，我们就能在这三个集合里，计算每个输入值的隶属度。如果一个人太瘦的隶属度为0，理想的隶属度为0.75，超重的隶属度为0.15。那我们可以推论，此人的体重是理想的，即75%（0.75）的隶属度。

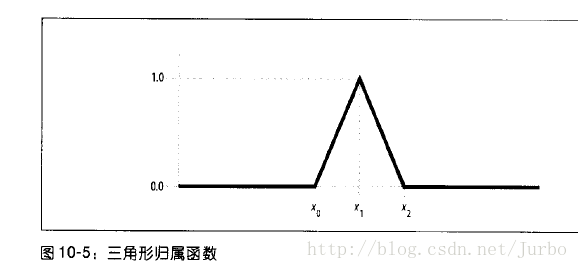
三角形归属函数也是除之前的直线型隶属函数（图10-3）之外，常用的隶属函数之一，如图 10-5 所示。

参考图10-5，此三角形隶属函数的方程式如下所示：

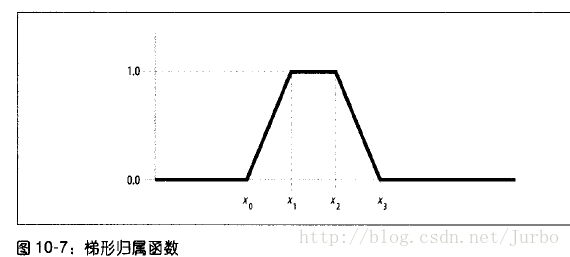
另一种常用的隶属函数是梯形隶属函数，如图10-7 所示。

梯形隶属函数的方程式如下所示：

到目前而言，我们讨论了3种最常用的线性隶属函数：直线型隶属函数（图10-3），三角形隶属函数（图10-5），梯形隶属函数（图10-7）。在要求较高精度或者有非线性需求时，有时候也会用到高斯曲线或者 S 形曲线。

例10-1 是我们讨论过的各个隶属函数的程序表示。

//例10-1：模糊逻辑中的隶属函数

//图10-3对应的直线型隶属函数
double FuzzyGrade(double value,double x0,double x1)
{
    double result=0;
    double x=value;

    if(x<=x0)
        result=0;
    else if(x>=x1)
        result=1;
    else
        result=(x/(x1-x0)) - (x0/(x1-x0));

    return result;
}

//图10-5对应的三角形隶属函数
double FuzzyTriangle(double value,double x0,double x1,double x2)
{
    double result=0;
    double x=value;

    if(x<=x0)
        result=0;
    else if(x==x1)
        result=1;
    else if( (x>x0) && (x<x1) )
        result=(x/(x1-x0)) - (x0/(x1-x0));
    else
        result=(-x/(x2-x1)) + (x2/(x2-x1));

    return result;
}

//图10-7对应的梯形隶属函数

double FuzzyTrapezoid(double value,double x0,double x1,double x2,double x3)
{
    double result=0;
    double x=value;

    if(x<=x0)
        result=0;
    else if( (x>=x1) && (x<=x2) )
        result=1;
    else if( (x>x0) && (x<x1) )
        result=(x/(x1-x0)) - (x0/(x1-x0));
    else
        result=(-x/(x3-x2)) + (x3/(x3-x2));

    return result;
}

想求出给定的输入值在特定集合内的隶属度，只需要调用例 10-1 的函数之一，并传递和该函数形状定义相关的数值和参数即可。

藩篱函数

藩篱函数有时候可以用于修改隶属函数所返回的隶属度。隶属函数主要提供其他的语汇素材，让你能在其他的逻辑运算中结合使用。两个常用的藩篱函数是 VERY( ) 和 NOT_VARY( )，其定义如下：

这里的 Truth(A) 就是 A 在某个模糊集合中的隶属度。隶属函数可以有效地改变隶属函数的形状。例如，把隶属函数用到线性隶属函数上时，会使隶属函数的线性部分变成非线性。

藩篱函数在模糊系统中不是必要的。我们可以构建隶属函数满足需要，不需要额外地再使用藩篱函数。在此提及，只是因为藩篱函数时常在模糊逻辑的领域里出现。

模糊规则

将明确的输入都模糊化后，接着要做的是构建一组规则，以某种逻辑方式结合输入数据，生成某些输出结果。

模糊公理

我们要能够处理交集（AND）、联集（OR），以及补集（NOT）。对于模糊变量来说，这些逻辑运算符的定义如下所示：

这里的 Truth（A）就是 A 在某模糊集合里的隶属度，其值介于0和1之间。Truth（B）则是 B 在某模糊集合里的隶属度。由此可见，OR 逻辑运算符被定义为操作数中的最大值，AND 逻辑运算符被定义成操作数中的最小值，NOT 运算符则是 1 减去 操作数的隶属度。

举个例子，假定某个对超重的隶属度是 0.7，对高的隶属度是0.3，则前述定义的逻辑运算符的结果会如下所示：

超重 AND 高 = MIN（0.7,0.3）=0.3
超重 OR  高 = MAX（0.7,0.3）=0.7
NOT 超重 = 1-0.7=0.3
NOT 高 = 1-0.3=0.7
NOT（超重 AND 高）= 1-MIN（0.7，0.3）=1-0.3=0.7

模糊逻辑运算符写成程序的话，则如例10-2 所示。

//例10-2：模糊逻辑运算符函数

double FuzzyAND(double A,double B)
{
    return MIN(A,B);    
}
double FuzzyOR(double A,double B)
{
    return MAX(A,B);
}
double FuzzyNOT(double A,double B)
{
    return 1.0-A;
}

模糊规则的评估运算

在传统逻辑的布尔系统中，每条规则会逐一运算，直到有条规则为真为止，然后就开始运行此结论。

在模糊逻辑的系统中，所有的规则都会同时进行运算，每条规则都会运行（因为每条规则都是部分真），然而，运行的强度或程度则各不相同。每条规则的前提的逻辑运算结果，会产生该规则结论的强度。换句话说，每条规则的强度代表的是输出的模糊集合中的隶属程度。

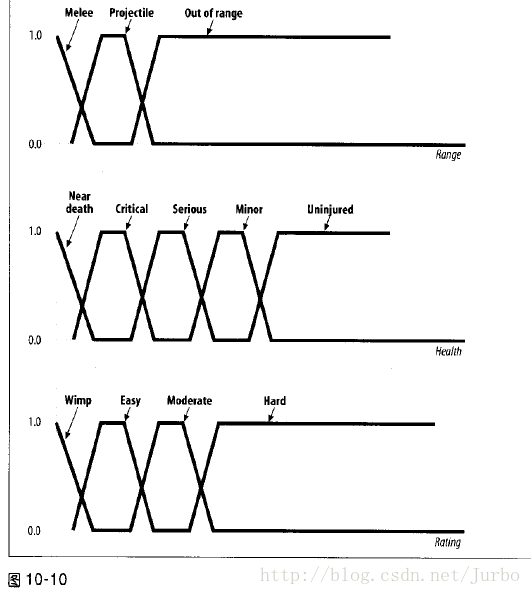
举个例子。我们使用模糊逻辑系统运算某生物是否应该攻击玩家。输入变量是距离，生物的健康状况，以及玩家的等级。每个变量的隶属函数如图10-10 所示。

此例中的输出行动可以是逃跑、攻击或什么也不做。我们可以写出类似下列语句的规则。

if(位于肉搏战距离内 AND 健康）AND NOT 坚强 then 攻击
if(NOT 位于肉搏战距离内）AND 健康 then 什么也不做
if(NOT 位于距离外 AND NOT 健康）AND （NOT 懦弱） then 逃跑

你也可以设定其他规则来处理其他的可能性。在你的游戏中，所有的规则都会运算，并获得每个输出结果的隶属度。每个输入变量都有隶属度后，你可能会得到如下所示的输出结果：

攻击的隶属度为0.2
什么也不做的隶属度为0.4
逃跑的隶属度为0.7

模糊规则如例10-3 所示，可以发现和传统的 if-then 形式的规则，有显著的差异。

degreeAttack=MIN( MIN (degreeMelee,degreeUninjured),1.0-degreeHard );

degreeDoNothing=MIN( (1.0-degreeMelee),degreeUninjured);

degreeFlee=MIN(MIN ((1.0-degreeOutOfRange),(1.0-degreeUninjured)),(1.0-degreeWimp) );

输出的程度代表的是每条规则的强度。解读输出结果的做法是以最高程度的行动为行动依据。就此例而言，最终行动是逃跑（因为逃跑的隶属度为0.7）。

反模糊化

当你想用精确数值作为模糊系统的输出数据时，就需要反模糊化的过程。

在前面我们说过，每条规则都会得到某个输出模糊集合中的隶属程度。就前例来说，假设此时不止要求出某种限定的行动的概率（什么也不做、逃跑或攻击），你还想输出结果，求出该生物采取行动时速率应该多大。例如，如果输出的行动是逃离，该生物是走着逃离，还是跑着逃离，而离开的速度有多快？要取得精确数值时，我们必须把输出强度聚集起来，也就是说需要定义输出隶属函数。

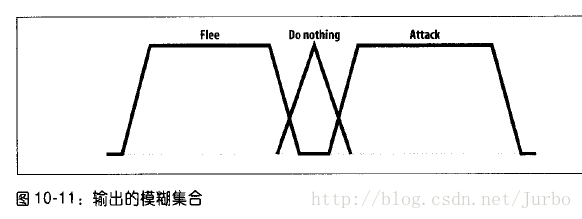
什么也不做、逃跑、攻击的输出隶属函数如图 10-11 所示。

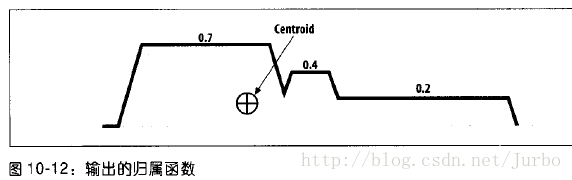
利用前面讨论过的数值输出（攻击的隶属度为0.2，什么也不做的隶属度为0.4，逃跑的隶属度为0.7），最后我们得到合成的隶属函数，如图10-12 所示。

为了得到合成的隶属函数，每个输出集合都按其规则强度，即所得到的输出隶属程度裁剪出来。然后，所有的输出集合再利用联集结合起来。

此时，我们只有输出的隶属函数，还没有精确数字。我们可以利用很多方法，从这样的输出模糊集合中得到精确数字。最常用的方法之一是，寻找输出模糊集合所占面积的几何中心，并以该中心的水平轴坐标值，作为精确输出值。这样就可以获得所有规则之间的妥协值，即单一输出数字，其实是所有输出隶属度的加权平均值。

要找出这种输出函数的中心，你得利用数值积分手段算出曲线围成的面积，或者可以想象成多边形，再用计算机以几何方法找到中心，也可以使用其他手段。

无论如何，找面积的中心是很耗费运算能力的，尤其是在游戏中运算次数会更多。所幸，有较为简单的方法可以利用，即单值输出隶属函数。

单值输出隶属函数，本质上是事先就反模糊化好的输出函数。例如，我们可以给每个输出行为指派速率，不如逃离是-10，什么也不做是1，攻击是10。就我们的例子而言，逃离行为最后所得的速率是 -10 乘以 0.7（逃跑的隶属度为0.7），即-7 为逃离速率。此时，计算所有输出值聚合起来的结果，只需要简单的加权平均值就行了，而不用再求中心了。

一般而言，假设 μ 是某输出几何为真的程度，x 为和此输出几何相关的精确单值，最最后聚合而反模糊化的输出结果是：

就我们的例子而言（攻击的隶属度为0.2，什么也不做的隶属度为0.4，逃跑的隶属度为0.7。逃离是-10，什么也不做是1，攻击是10），最后所得结果如下：

输出值= [ 0.7*(-10) + (0.4)*1+(0.2)*(10) ] / (0.7+0.4+0.2)