3.傅里叶变换推导 [学习笔记]

在前几篇笔记中，我们推导了傅里叶级数相关公式，这次的笔记将进行傅里叶变换的推导
傅里叶变换的核心思想是：将任意非周期函数看作周期无限长的周期函数，因此可以调用傅里叶级数的相关公式

我们不妨设$f(t)$为周期$T$的信号函数，先导出：

$$\begin{align*} f(t) &= \sum_{k=-\infty}^\infty C_k e^{2\pi ik(\frac{t}{T})} \\ &= \sum_{k=-\infty}^\infty C_k e^{2\pi i(\frac{k}{T})t} \tag1 \end{align*}$$

运用和傅里叶级数的系数推导过程相同的方法（详见傅里叶级数推导过程中的$C_k$推导），我们有：

$$\begin{align*} \int_{-\frac{T}{2}}^{\frac{T}{2}} C_mdt &= \int_{-\frac{T}{2}}^{\frac{T}{2}}f(t)e^{-2\pi im(\frac{t}{T})}dt -\sum_{k \neq m}C_k \int_{-\frac{T}{2}}^{\frac{T}{2}}e^{2\pi i(k-m)(\frac{t}{T})}dt\\ &=\int_{-\frac{T}{2}}^{\frac{T}{2}} e^{-2\pi im(\frac{t}{T})} f(t)dt - 0\\ &=\int_{-\frac{T}{2}}^{\frac{T}{2}} e^{-2\pi i(\frac{m}{T})t} f(t)dt \end{align*}$$

等式左边为$TC_m$，因此对于任意k，我们移项后可以得到：

$$C_k = \frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}} e^{-2\pi i(\frac{k}{T})t} f(t)dt \tag2$$

---

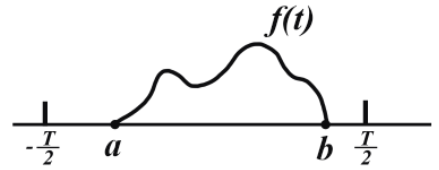
我们假设函数在区间$[a,b]$内大于等于零，其余均为零，则我们令周期大于等于$a-b$的长度，并将其包围，如下图

接下来，我们正式开始推导傅里叶变换
注意，当$T\to \infty$时，如果我们直接用$(2)$式进行推导：

$$\begin{align*} C_k &= \frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}} e^{-2\pi i(\frac{k}{T})t} f(t)dt\\ &= \frac{1}{T}\int_a^b e^{-2\pi i(\frac{k}{T})t} f(t)dt \end{align*}$$

当我们对$C_k$取模时（由高等数学知识，我们知道积分的绝对值小于等于绝对值的积分），

$$\left \lvert C_k \right \rvert \leq \frac{1}{T}\int_a^b \left \lvert e^{-2\pi i(\frac{k}{T})t} \right \rvert \left \lvert f(t) \right \rvert dt$$

由欧拉公式，我们可以知道$e^{ix}$的模长总为$1$（复数的模长等于其实部与虚部的平方的平方根），因此我们有：

$$\left \lvert C_k \right \rvert \leq \frac{1}{T}\int_a^b \left \lvert f(t) \right \rvert dt$$

等式的右边的积分$\int_a^b \left \lvert f(t) \right \rvert dt$为定积分，因此当$T\to \infty$时，$C_k \to 0$

显然这个结果对实际应用而言毫无意义，直接带入并求极限并不能得到我们需要的结果。因此我们换用以下方式：

首先，我们定义

$${\scr F}f(\frac{k}{T}) = \int_{-\frac{T}{2}}^{\frac{T}{2}} e^{-2\pi i(\frac{k}{T})t} f(t)dt$$

那么$(2)$、$(1)$式就可以分别改写为：

$$C_k = \frac{1}{T} {\scr F}f(\frac{k}{T})$$

$$f(t) = \sum_{k=-\infty}^\infty \frac{1}{T} {\scr F}f(\frac{k}{T}) e^{2\pi i(\frac{k}{T})t}$$

我们发现，当$T\to \infty$时，$\frac{1}{T}$就成为了一个连续变量的$\Delta s$，而$\frac{k}{T}$就可以写为自变量$s$（这里我们将其设为$s$），不难发现，这就是我们对于积分的定义。因此,当$T\to \infty$时，我们有:

$$f(t) = \int_{-\infty}^\infty e^{2\pi ist} {\scr F}f(s)ds\tag3$$

$${\scr F}f(s) = \int_{-\infty}^\infty e^{-2\pi ist} f(t)dt\tag4$$

放到信号系统中，$t$表示时间，$s$代表频率，因此，就有了时域和频域的区别；
但是要注意的是傅里叶变换并不一定是时间和频率的关系，其他变量也可以作为傅里叶变换的对象，如空间坐标$x$等等

由$(4)$、$(3)$两式，我们可以得到傅里叶变换及傅里叶逆变换：

$${\scr F}f(s) = \int_{-\infty}^\infty e^{-2\pi ist} f(t)dt$$

$${\scr F}^{-1}g(t) = \int_{-\infty}^\infty e^{2\pi ist} g(s)ds$$