在讲题之前我把有关欧拉回路的知识点先整理出来,如下:
知识锦囊
欧拉路径: 在图 G 中包含每条边各一次的路径
欧拉回路:在图 G 中从起点出发包含每条边各一次且最终回到起点的路径(就是如果一个欧拉路径的起始点相同,那就是一个欧拉回路)
欧拉图: 含有欧拉回路的图
半欧拉图: 含有欧拉路径,没有欧拉回路的图
简单路径: 除起点和终点可以相同以外,所有简单路径上的点都只被经过一次(只出现一次)
简单回路: 起点和终点相同的简单路径
总的来说就是简单路径是每个点只访问一次,欧拉路径是每条边只访问一次
现在我们来看看如何判断一个图是否为欧拉图:
分为无向图和有向图来考虑
若为无向图,则需满足条件:
- 这个图必须连通(这显而易见)
- 每个顶点的度数为偶数(因为每个点“进”“出”的次数相同,所以必为偶数)
(若将 条件2 改为只有两个点的度数为奇数,那就是判断一个半欧拉图了)
若为有向图,则需满足条件:
- 这个图的基图是连通的(所谓基图,就是有向图不考虑边的方向,当做无向图来看)
- 每个顶点的出度和入度相等
(若将 条件2 改为只有两个点的出度和入度不一样,且起点 -->出度=入度+1,终点 -- > 出度=入度 - 1,那就是判半欧拉图)
那么判断倒是很容易,如果要输出欧拉回路的路径呢,这个怎么搞?
据说有两种方法可以达到目的,但我们只讲更优秀的那一个就够了,另外一个的话,嘿嘿,可以去这里看一下,讲的很好,下面的我也是摘自这个博客,真的写的好棒
基本(套圈)法
首先从一个节点(v0)出发,随便往下走(走过的边需要标记一下,下次就别走了),当走到不能再走的时候,所停止的点必然也是起点(因为所有的点的度数都是偶数,能进去肯定还会出来,再者中间有可能再次经过起点,但是如果起点还能继续走,那么就要继续往下搜索,直到再次回来时不能往下搜索为止),然后停止时,走过的路径形成了一个圈,但因为是随便走的,所以可能有些边还没走就回来了,那些剩下的边肯定也会形成一个或者多个环,然后可以从刚才终止的节点往前回溯,找到第一个可以向其他方向搜索的节点(vi),然后再以这个点继续往下搜索,同理还会继续回到该点(vi),于是这个环加上上次那个环就构成了一个更大的环,即可以想象成形成了一条从 v0 到 vi的路径,再由 vi 走了一个环回到 vi,然后到达v0 的一条更长的路径,如果当前的路径还不是最长的,那么继续按照上面的方法扩展。只需要在回溯时记录下每次回溯的边,最后形成的边的序列就是一条欧拉回路。如果要记录点的顺序的话,那么每访问一个点,就把这个点压入栈中,当某个点不能继续搜索时,即在标记不能走的边是,这个点成为了某种意义上的孤点,然后把这个点输出最后得到的就是一条欧拉回路路径的点的轨迹。
总之,求欧拉回路的方法是,使用深度优先搜索,如果某条边被搜索到,则标记这条边为已选择,并且即使回溯也不能将当前边的状态改回未选择,每次回溯时,记录回溯路径。深度优先搜索结束后,记录的路径就是欧拉回路。
下面用图描述一遍:
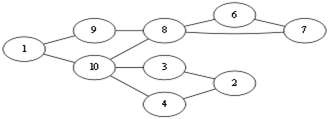
假设我们选择从v1开始走,由于随便走,所以可能出现以下走法
第一步:v1 -- v9
第二步:v9 -- v8
第三步:v8 -- v10
第四步:v10 -- v1
此时由于走过的边不能再走,那么从 v1 就无法继续向下探索,所以往前回溯,记录边集Eu{<v1, v10>},此时回溯到 v10 ,发现可以继续走,那么
第五步: v10 -- v3
第六步: v3 -- v2
第七步: v2 -- v4
第八步: v4 – v10
发现已经无路可走,那么继续回溯,记录回溯路径得到Eu{<v1,v10>, <v10, v4>, <v4, v2>, <v2, v3>, <v3, v10>, <v10, v8>},此时回溯到了 v8.发现可以向其他方向搜索, 那么
第九步:v8 -- v6
第十步:v6 --v7
第十一步:v7-- v8
又无路可走,继续回溯Eu{<v1,v10>, <v10, v4>, <v4, v2>, <v2, v3>, <v3, v10>, <v10, v8>, <v8, v7>, <v7, v6>,<v6,v8>,<v8,v9>,<v9,v1>},到这里整个DFS就结束了,我们得到的边集Eu就是一条欧拉回路。
摘毕。。。。。。。。。。。。。。。。。。。。。。。。。。。。。
这里小bi一句:其实很多算法只要你愿意花时间去模拟一遍,就能理解了
下面开始讲题:
这次我们先看一下代码,毕竟就只是一个裸的欧拉回路模板题,没什么好分析的,代码中会解释一些骚操作
代码:
#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<iostream>
#include<cstdlib>
#include<vector>
#define M 400009
#define N 100009
#define inr read()
using namespace std;
int type,n,m;
int nxt[M],head[N],to[M],cnt=1;
int in[N],out[N];
bool vis[M];
vector<int> ans;
void add(int x,int y){ nxt[++cnt]=head[x];head[x]=cnt;to[cnt]=y; }
inline int read(){
char ch;int f=1,res=0;
while((ch=getchar())<'0'||ch>'9')
if(ch=='-') f=-1;
while(ch>='0'&&ch<='9'){
res=(res<<1)+(res<<3)+ch-'0';
ch=getchar();
}
return f==1?res:-res;
}
void dfs(int u){
for(int &e=head[u];e;e=nxt[e]){//当前弧优化(学过网络流的就明白,没学过的。。自己查吧)
int v=to[e],c=(type==1?(e/2):(e-1));//后面单独讲一下
int sign=e&1;
if(vis[c]) continue;
vis[c]=1;
dfs(v);
if(type==1) ans.push_back(sign==1?-c:c);
else ans.push_back(c);
}
}
int main(){
type=inr;n=inr;m=inr;
int i,j,k;
for(i=1;i<=m;++i){
int u,v;
u=inr;v=inr;
add(u,v);
out[u]++;in[v]++;//记录出度和入度
if(type==1) add(v,u);
}
if(type==1){
for(i=1;i<=n;++i)
if((in[i]+out[i])&1){ // x&1,是判断 x 的奇偶,x&1==1,则说明x为奇数
printf("NO");
return 0;
}
}
else{
for(i=1;i<=n;++i)
if(in[i]!=out[i]){//有向图:出度不等于入度
printf("NO");
return 0;
}
}
for(i=1;i<=n;++i)
if(head[i])//要排除孤立点,找到第一个不是孤立点的点
{
dfs(i);
break;
}
if(ans.size()!=m) {printf("NO");return 0;}//如果刚刚找到的欧拉回路并没有包含所有的边,
//那么说明刚刚找到的只是图中的一个子图,说明整个图除了孤立点以外仍旧不连通那么肯定不是欧拉图
printf("YES\n");
for(i=m-1;i>=0;--i)//倒着输出,如果明白了之前模拟的算法过程就知道为什么了
printf("%d ",ans[i]);
return 0;
}来单独讲一下这一步:c=(type==1?(e/2):(e-1));
之所以可以这样处理是因为我们是从2开始存的边
那么如果是从1开始存边就应该这样写:c=(type==1?(e%2==0?e/2:(e+1)/2):e)
是不是好写的多?
这个 c 表示的就是这条边本来的编号,你想咯,无向边存了两遍,但实际上还是指的同一条边,可以举几个例子自己看看