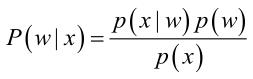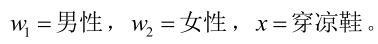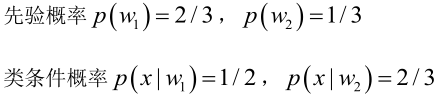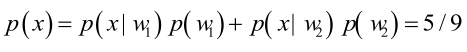【数学基础】参数估计之极大似然估计

背景

先来看看几个小例子：

猎人师傅和徒弟一同去打猎，遇到一只兔子，师傅和徒弟同时放枪，兔子被击中一枪，那么是师傅打中的，还是徒弟打中的？
一个袋子中总共有黑白两种颜色100个球，其中一种颜色90个，随机取出一个球，发现是黑球。那么是黑色球90个？还是白色球90个？

看着两个小故事，不知道有没有发现什么规律...由于师傅的枪法一般都高于徒弟，因此我们猜测兔子是被师傅打中的。随机抽取一个球，是黑色的，说明黑色抽中的概率最大，因此猜测90个的是黑色球。

他们有一个共同点，就是我们的猜测（估计），都是基于一个理论：概率最大的事件，最可能发生。

其实我们生活中无时无刻不在使用这种方法，只是不知道它在数学中是如何确定或者推导的。而在数理统计中，它有一个专业的名词：极大似然估计（maximum likelihood estimation, MLE），通俗的说就是 —— 最像估计法（最可能估计法）

贝叶斯决策

首先来看贝叶斯分类，我们都知道经典的贝叶斯公式：

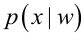
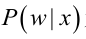
其中：p(w)：为先验概率，表示每种类别分布的概率；：类条件概率，表示在某种类别前提下，某事发生的概率；而为后验概率，表示某事发生了，并且它属于某一类别的概率，有了这个后验概率，我们就可以对样本进行分类。后验概率越大，说明某事物属于这个类别的可能性越大，我们越有理由把它归到这个类别下。

我们来看一个直观的例子：已知：在夏季，某公园男性穿凉鞋的概率为1/2，女性穿凉鞋的概率为2/3，并且该公园中男女比例通常为2:1，问题：若你在公园中随机遇到一个穿凉鞋的人，请问他的性别为男性或女性的概率分别为多少？

从问题看，就是上面讲的，某事发生了，它属于某一类别的概率是多少？即后验概率。

设：

由已知可得：

扫描二维码关注公众号，回复： 2776117 查看本文章

男性和女性穿凉鞋相互独立，所以

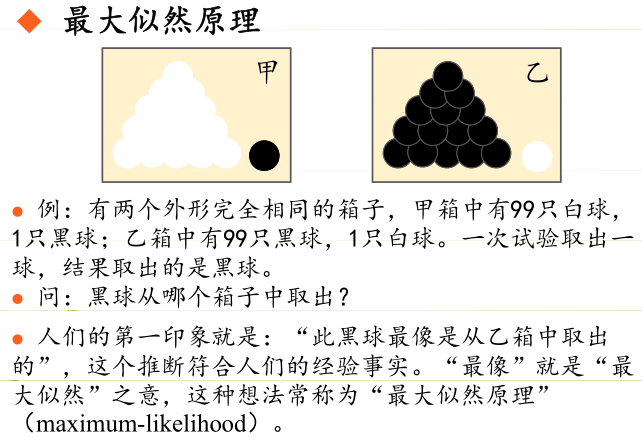
由贝叶斯公式算出：

贝叶斯公式就是在描述，你有多大把握能相信一件证据？（how much you can trust the evidence）

在这个问题中贝叶斯公式描述的就是你有多大的把握相信穿了凉鞋的这个人是男生或者女生。

同时从另一个角度解释贝叶斯公式，做判断的时候，要考虑所有的因素。

讲的就是不能因为女生穿凉鞋的概率高你就认为穿拖鞋的都是女性，你还要考虑到其它因素，比如题目中给的男女比例，如果比例在夸张一点，100个人里面才有1个女的，即使女性穿拖鞋的概率是100%，穿拖鞋的人是个女生的概率也是很小。

从这个角度思考贝叶斯公式：一个本来就难以发生的事情，就算出现某个证据和他强烈相关，也要谨慎。证据很可能来自别的虽然不是很相关，但发生概率较高的事情。

性别于穿不穿凉鞋的相关性很强，但就如上面取那个极端男女比例的例子一样，男女比例的高低于穿不穿凉鞋没有半毛钱关系，（你就想穿凉鞋的人多了男女比例能上升或者下降吗？反过来就有关系了，有的时候关系很复杂，一时间看不出来就是这个道理，比如你今天工作效率低被老板教训了，但谁知道老板教训你的真正原因是不是早上老板的老婆大人教训了他一顿呢？）但有的时候真正影响结果的原因就是来自这些不是很相关的东西，因其能影响某些事件的概率。

问题引出

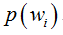
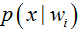
但是在实际问题中并不都是这样幸运的，我们能获得的数据可能只有有限数目的样本数据，而先验概率和类条件概率(各类的总体分布)都是未知的。根据仅有的样本数据进行分类时，一种可行的办法是我们需要先对先验概率和类条件概率进行估计，然后再套用贝叶斯分类器。

先验概率（如这里的男女比例）的估计较简单：

每个样本所属的自然状态都是已知的（有监督学习）；
依靠经验；
用训练样本中各类出现的频率估计。

类条件概率的估计（非常难，如这里的男性穿凉鞋的概率，女性穿凉鞋的概率），原因包括：

概率密度函数包含了一个随机变量的全部信息；
样本数据可能不多；
特征向量x的维度可能很大等等。

总之要直接估计类条件概率的密度函数很难。

解决的办法就是，把估计完全未知的概率密度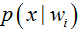转化为估计参数。这里就将概率密度估计问题转化为参数估计问题，极大似然估计就是一种参数估计方法。当然了，概率密度函数的选取很重要，模型正确，在样本区域无穷时，我们会得到较准确的估计值，如果模型都错了，那估计半天的参数，肯定也没啥意义了。

重要前提

上面说到，参数估计问题只是实际问题求解过程中的一种简化方法（由于直接估计类条件概率密度函数很困难）。所以能够使用极大似然估计方法的样本必须需要满足一些前提假设。

重要前提：

训练样本的分布能代表样本的真实分布。
每个样本集中的样本都是所谓独立同分布的随机变量 (iid条件)，
且有充分的训练样本。

极大似然估计（Maximum Likelihood Estimate,MLE）

极大似然估计的原理，用一张图片来说明，如下图所示：

总结起来，最大似然估计的目的就是：利用已知的样本结果，反推最有可能（最大概率）导致这样结果的参数值。

原理：极大似然估计是建立在极大似然原理的基础上的一个统计方法，是概率论在统计学中的应用。极大似然估计提供了一种给定观察数据来评估模型参数的方法，即：“模型已定，参数未知”。通过若干次试验，观察其结果，利用试验结果得到某个参数值能够使样本出现的概率为最大，则称为极大似然估计。

这里先以一个分类问题来说明一般参数估计面对的数据形式。考虑一个 $M$ 类的问题，特征向量服从 $p(x|\omega_i),i=1,2...,M$ 分布。这是现实情况中最常见的一种数据存在形式，数据集合 $X$ 是由 $M$ 个类别的数据子集 $X_m,m=1,2...,M$ 组成的，第 $m$ 类别的数据子集 $X_m$ 对应的概率密度函数是 $p(x|\omega_m)$ 。

前面已经介绍过了，想要确定数据的概率分布，需要知道概率密度函数的形式和参数，这里首先做一个基本假设：概率分布的形式已知，比如假设每个类别的数据都满足高斯分布，那么，似然函数就可以以参数 $\theta_i$ 的形式表示，如果是高斯分布，则参数为 $\mu_i$ 和 $\sigma^2_i$ ，即 $\theta_i=(\mu_i,\sigma_i^2)$ 。

为了强调概率分布 $p(x|\omega_i)$ 和 $\theta_i$ 有关，将对应的概率密度函数记为 $p(x|\omega_i;\theta_i)$ ，

注意，这里 $p(x|\omega_i;\theta_i)$ 不等同于 $p(x|\omega_i,\theta_i)$ ，前者 $\theta$ 默认为是一个固定的值，一个本身就存在的最佳参数矩阵；而后者认为 $\theta$ 是一个变量（统计学中frequentist和Bayesian的差别）。

白话文又来了。

$p(x|\omega_i;\theta_i)$ 其实等同于 $p(x|\omega_i)$ （这是一个条件概率，在 $w_i$ 类时 $x$ 事件发生的概率）， $\theta_i$ 作为一个待估参数其实是已经确定的，即使还不知道。

$p(x|\omega_i,\theta_i)$ 不能够化简，此时是关于变量 $w_i,\theta_i$ 的条件概率，表示在这两个变量确定的情形下，事件 $x$ 发生的概率， $\theta_i$ 是一个变量并不是一个固定的参数。

该记法属于频率概率学派的记法。这里的极大似然估计对应于一个类条件概率密度函数。

在概率论中一直有两大学派，分别是频率学派和贝叶斯学派。简单点说，频率学派认为，概率是频率的极限，比如投硬币，当实验次数足够大时，正面朝上的频率可以认为是这枚硬币正面朝上的概率，这个是频率学派。但是，如果要预测一些未发生过的事情，比如，北极的冰山在2050年完全融化的概率，由于这个事情完全没有发生过，所以无法用频率来代替概率表示，只能研究过去几十年，北极冰山融化的速率，并将其作为先验条件，来预测北极的冰山在2050年完全融化的概率，这就是概率的贝叶斯学派。上面的问题，如果用贝叶斯学派的记法的话，是： $p(x|\omega_i,\theta_i)$ 。这两个学派适用的情况不太一样，但是，在我目前所用到的概率论的知识中，貌似这两个学派并没有什么太大的区别，只是记法略有不同，稍微注意下即可。

从上面的描述中可以知道，利用每一个类 $X_i$ 中已知的特征向量集合，可以估计出其对应的参数 $\theta_i$ 。进一步假设每一类中的数据不影响其他类别数据的参数估计，那么上面的 $M$ 个类别的参数估计就可以用下面这个统一的模型，独立的解决：

设 $x_1,x_2,...,x_N$ 是从概率密度函数 $p(x;\theta)$ 中随机抽取的样本，那么就可以得到联合概率密度函数 $p(X;\theta)$ ，其中 $X=\{x_1,x_2,...,x_N\}$ 是样本集合。假设不同的样本之间具有统计独立性，那么：

$p(X;\theta)\equiv p(x_1,x_2,...,x_N;\theta)=\prod_{k=1}^Np(x_k;\theta)$

注意：这里的 $p(x_k;\theta)$ 本来的写法是 $p(x_k|\omega_i;\theta_i)$ , 是一个类条件概率密度函数，只是因为这里是一个统一的模型，所以可以将 $w_i$ 省略。（统一的意思就是 $p(x_k;\theta)=\sum _{i=1}^M p(x_k|\omega_i;\theta_i)$ ）

需要重申一下，想要得到上面这个公式，是做了几个基本的假设的，第一：假设 $M$ 个类别的数据子集的概率密度函数形式一样，只是参数的取值不同；第二：假设类别 $i$ 中的数据和类别 $j$ 中的数据是相互独立抽样的，即类别 $j$ 的参数仅仅根据类别 $j$ 的数据就可以估计出来，类别 $i$ 的数据并不能影响类别 $j$ 的参数估计，反之亦然；第三：每个类别内的样本之间具有统计独立性，即每个类别内的样本之间是独立同分布 (iid) 的。

此时，就可以使用最大似然估计(Maximum Likelihood Estimate,MLE)来估计参数 $\theta$ 了：

$\hat{\theta}_{ML}=arg\max_{\theta}\prod_{k=1}^Np(x_k;\theta)$

似然函数为：

$L(\theta)=\prod_{k=1}^Np(x_k;\theta)$

为了得到最大值， $\hat{\theta}_{ML}$ 必须满足的必要条件是,似然函数对 $\theta$ 的梯度必须为0，即：

$\frac{\partial L(\theta)}{\partial \theta}=\frac{\partial \prod_{k=1}^Np(x_k;\theta)}{\partial\theta}=0$

一般我们取其对数形式：

$\ell(\theta)=ln L(\theta)\equiv ln\prod_{k=1}^Np(x_k;\theta)=\sum _{k=1}^Nlnp(x_k;\theta)$

$\frac{\partial \ell(\theta)}{\partial \theta}=\sum_{k=1}^N \frac{\partial ln p(x_k;\theta)}{\partial \theta}=\sum_{k=1}^N\frac{1}{p(x_k;\theta)} \frac{\partial p(x_k;\theta)}{\partial \theta}=0$

需要注意：极大似然估计对应于似然函数的峰值

极大似然估计有两个非常重要的性质：渐进无偏 和 渐进一致性，有了这两个性质，使得极大似然估计的成为了非常简单而且实用的参数估计方法。这里假设 $\theta_0$ 是密度函数 $p(x;\theta)$ 中未知参数的准确值。

渐进无偏

极大似然估计是渐进无偏的，即：

$\lim_{N \to \infty}E[\hat{\theta}_{ML}]=\theta_0$

也就是说，这里认为估计值 $\hat{\theta}_{ML}$ 本身是一个随机变量（因为不同的样本集合 $X$ 会得到不同的 $\hat{\theta}_{ML}$ ），那么其均值就是未知参数的真实值，这就是渐进无偏。

渐进一致

极大似然估计是渐进一致的，即：

$\lim_{N \to \infty}prob\{ \lVert \hat{\theta}_{ML}- \theta_0 \rVert \leqslant \epsilon\} = 1$

这个公式还可以表示为：

$\lim_{N \to \infty} E \lVert \hat{\theta}_{ML}- \theta_0 \rVert^2 = 0$

对于一个估计器而言，一致性是非常重要的，因为存在满足无偏性，但是不满足一致性的情况，比如， $\hat{\theta}_{ML}$ 在 $\theta_0$ 周围震荡。如果不满足一致性，那么就会出现很大的方差。

注意：以上两个性质，都是在渐进的前提下（ $N \to \infty$ ）才能讨论的，即只有NN足够大时，上面两个性质才能成立。

一个简单的例子

经典的例子是抛硬币，这里换一个差不多的。

已知总体X是离散型随机变量，其可能的取值是0、1、2。且

对X抽取容量为10的样本，其中2个取0，5个取1，3个取2。

求θ的最大似然估计值。

解法：

其实就是找到使得 2个取0，5个取1，3个取2的可能性最大的θ。

2个取0，5个取1，3个取2的可能性，用下面的似然函数来衡量：

然后，转化为：

令：

可以得到θ的最大似然估计值为9/20。

参考文章：

贝叶斯线性回归（Bayesian Linear Regression）

线性回归概率解释(Linear Regression)

极大似然估计详解