在我上一次发表的第一篇博客上,讲了一些关于线段树的入门和基本应用,所以在继续拓展线段树的应用之前,我们先给大家讲一下线段树在树形结构当中的应用(不会线段树的同学们可以看看我上次的博客:http://blog.csdn.net/amuseir/article/details/79301619)
在算法竞赛当中,树形结构是一种十分常考的数据类型,而在它们当中,有一种非常重要的问题,便是数的统计和查询,那我们在这里列出一些比较基本的树形结构的操作(它们之中很多与线段树十分类似,这就是为什么我在刚刚讲完线段树后补充讲这些内容)
1、单点修改、子树查询。
2、子树修改、单点查询。
3、子树修改,子树查询。
4、单点修改、链查询。
5、链修改,子树查询。
6、链修改、链查询。
第六条其实是前五条的通常情况(实质上,所有点都是只有单点的链,所以是一种特殊情况),所以最后一条的操作会稍微有些繁琐(最后一条的话只会dfs序是没有办法的,最好用树链剖分,这个坑我应该过段时间也会一起填上去),我们今天就讲一讲前五条的操作方法。
我们要明白,要搞定前三条操作的话,需要先搞清楚dfs序这个概念。
dfs序分为三种(n个节点、2*n-1个节点、2*n个节点)
首先我们看看第一种n个节点的,这是最最最最实用、可操作性最强、以及最常见的操作类型(实质上是因为另外两种基本没有任何卵用),介于这个结构比较特殊,我们需要先弄清楚搞出这个dfs序的结构需要一些什么东西才能够明白原因。
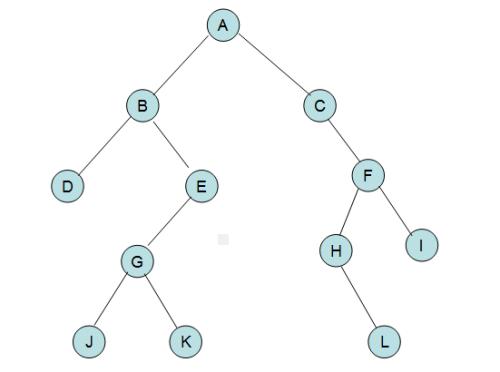
我们现在随机给你一颗树
现在如果我们要从根节点开始进行dfs深度搜索的话,它的n个节点的dfs序可以是(注意,并不是一定,因为在实际的题目的操作中我们是用邻接链表来完成的,所以很多节点的顺序可能不一样,但是在这个dfs序中,顺序对我们要做的事情并没有影响)这样的:ABDEGJKCFHLI(这里看上去很像是先序遍历,但是实际上);
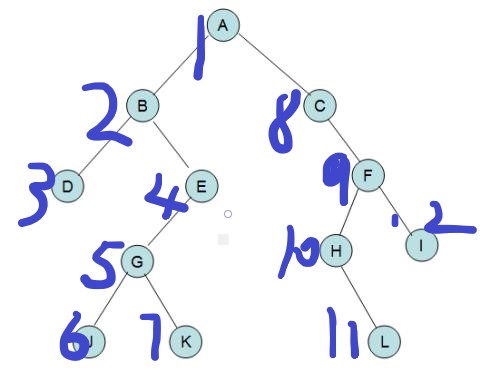
我们在这个dfs序的结构当中需要设置三个特殊数组,第一个叫做seq[],它的作用是储存原来的数对应到dfs序上的结果,(就是把原来数上节点的信息在dfs序的时候搬进去,就像就可以把图中的树搬到那个ABDECF上一样,图中的A就对应seq[1]是A,seq[4]是E,所以在之后的内容里,为了方便大家的理解,我在树中把每个节点对应的seq下标标出来吧)
第二个数组叫做in[],它储存的是每一个节点进入seq时候它对应的下标,比如对于B来说,in[B]是2,对于F来说,in[F]是9(就是这个元素本身在数组中的下标)
第三个数组,也是最重要的一个,out[],在这个数组中的out[]代表了当一个元素在dfs中,它的子树已经在深搜完成遍历过后,返回它的时候,seq[]里最后一个元素所对应的位置(听起来很难理解是不?但是我举两个例子就相当简单了)
在图中,out[A]是12,out[B]是7,out[5]也是7,out[C]是12,以此类推(实际上out[某个节点]就是这个节点的子树里最后一个被遍历节点的dfs序,所以说,每一个节点的seq[in【】]到seq[out【】]就是这个节点到它的所有子树)
那么我们就可以发现一个非常神奇的地方,对于任意的一个节点,由于out【这个节点】是它返回它之前的那个节点的下标,也就意味着肯定是它子树里最后一个被遍历的节点所对应的位置,而in【】是它进入时候的位置,所以我们一开始就使用dfs的方式将整颗树里的信息全部储存到数组seq里,我们就可以利用这个seq【】来建线段树,然后通过对于线段树的操作,完成对某一个节点以及其子树的修改和查询。
那么由此可见,我们想要建立dfs序的结构需要的最重要的条件就是:
需要知道关于这颗树上所有节点的连接关系(如果建不出来邻链表的话这个结构是无法实现的)
代码实现如下
首先是建立邻接链表的方式(其实很简单啦,对图论有点了解的应该都是会的)(我这里用的是结构体,当然也可以用数组模拟)。
#include<bits/stdc++.h>
using namespace std;
const int MAXN=100000+5;
struct Edge
{
int nxt;//下一条要访问的边
int to;//当前的边要通向的节点
int dis;//当前的边所对应的权值,可能是边权或者点权(注意,在一般的题里面,我们会将点权转换成边权来表示)
}edge[MAXN*2];//树是无向图,所以说我们要定义两倍
int head[MAXN*2];
int num=0;//在建立邻链表的时候统计边数的东西。。。。
void add(int from ,int to ,int dis )
{
edge[++num].nxt = head[from];
edge[num].to=to;
edge[num].dis=dis;
head[from]=num;
} 在主函数中,我们需要的就是输入节点和权值,然后用add操作就行啦。
而在访问的时候,我们就这样:
void vis(int u)//访问与u相连接的所有边
{
for(int i=head[u];i;i=edge[i].nxt)
{
//然后在每一次进行各种操作就行啦
}
}实际上,由于树本身就是一种特殊的无向图,所以我们可以使用以上的操作方式,当然,另一个方面,我们也可以直接用建二叉树的方式来建立和访问,但是那个样子代码贼长就不说了,而且相当慢(如果你知道用new申请节点会卡掉多少时间的话。。。。)
接下来,我们来看一下最重要的操作吧(在铺垫这么多之后,终于开始dfs序本身的代码实现啦)
void dfs(int u,int f)//f是u的父亲节点,因为用邻链表存图理所当然会遍历所有相关的边(包括父亲节点),为了防止出问题就在这里把变量带入
{
seq[++idc]=u;//idc的初值是赋的0
in[u]=idc;
for(int i=head[u];i;i=edge[i].nxt)
{
int v=edge[i].to;
if(v==f) continue;
dfs(v,u);
}
out[u]=idc;
}
void build()//建立seq操作如下
{
idc=0;
dfs(root,root)//假设root是根节点
} 那么其在线段树的建树操作与正常情况基本是一致的,部分代码实现如下
const int N=10000+6;
struct Node
{
long long sum;
bool flag;
long long tag;//用int还是long long看题而定
Node *ls;
Node *rs;
void update()
{
sum=ls->sum+rs->sum;
}
void pushdown(int l,int r)
{
if(flag)
{
int mid=(l+r)>>1;
ls->tag+=tag;
rs->tag+=tag;
ls->flag=rs->flag=1;
ls->sum+=(mid-l+1)*tag;
rs->sum+=(r-mid)*tag;
flag=0;
}
}
}pool[2*N],*tail=pool,*root;
Node *build(int l,int r)
{
Node *nd=++tail;
if(l==r)//
{
nd->sum=seq[l];// 这是与裸题建树唯一不同的地方
nd->flag=0;
nd->tag=0;//这里的步骤是赋初值,我们要注意,低版本c++不能再结构体内部赋初值的,所以考试的时候千万要在函数里赋
}
else
{
int mid=(l+r)>>1;//位运算操作符,效果等同于(l+r)/2
nd->ls=build(l,mid)//更新左右儿子
nd->rs=build(mid+1,r);
nd->update();
}
return nd;//把当前位置的值返回上去
}
void tree_build()
{
root=build(1,idc);//注意,idc的长度其实就是n,所以就用build(1,n)也行的
} 用这样建立起来的dfs序结构,就可以解决前三个问题了。
修改和查询操作的函数仍然与一般线段树无异,只不过在题目中,如果要让你查询一个节点及其子树的和/max等等的时候,query内的L和R就是in[u]和out[u]
仍然是用代码来举例子比较合适
long long query(Node *nd,int l,int r,const int L,const int R)//就是一般的查询操作啦,详情可以参见我开头的链接,有我上一次的代码作参考
{
if(L<=l&&R>=r)
{
return nd->sum;//这里只是用sum来做例子,最大值最小值都是可以的啦
}
int mid=(l+r)>>1;
nd->pushdown(l,r);
long long ans=0;
if(L<=mid) ans+=query(nd->ls,l,mid,L,R);
if(mid<R) ans+=query(nd->rs,mid+1,r,L,R);
return ans;
}
void tree_build()
{
root=build(1,idc);//注意,idc的长度其实就是n,所以就用build(1,n)也行的
}
long long son_query(int u)//查询某个节点u以及其子树
{
return query(root,1,idc,in[u],out[u])//由于in[]到out[]就是它的子树,我们就查询这一段就可以轻松解决问题
}而第4条和第5条,则要涉及到最近公共祖先(lca)这一个重要的概念。
首先,我们要明白lca到底是什么意思,其实lca是 the least common ancestor的缩写,我们定义,当在一棵树T内,如果一个节点u在a到根节点的最短路径上,我们就称u是a的祖先,举个例子:
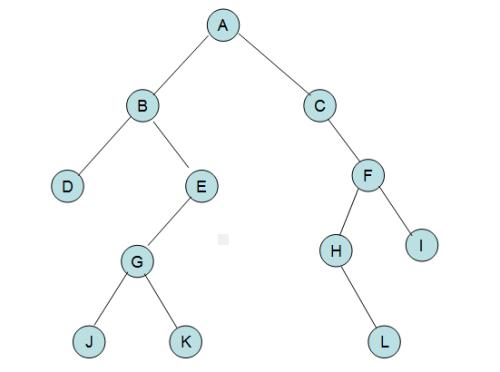
还是这一张图,对于J来说,到根节点的最短路径是J->G->E->B->A,所以说G、E、B、A都是J的祖先,公共祖先则是两个或者多个节点共同拥有的祖先,而由于A是根节点,所以说A是所有节点的祖先(也就是说A点是所有节点的公共祖先)。
而最近的公共祖先的意思相当明确,就是两个点的公共祖先中离这两个点深度最大的(其实就是离它们最近的啦= =),比如说L和I的lca是F,J和K的lca是G,D和L的lca是A。
那么我们可以先告诉大家一个规律,对于任何一条链,我们都可以用根节点的子树配合这条链的起始位置和终点的lca来表示。
仍然是在这张图内,由于我们在dfs序内建立的是一颗树的子树的信息集合,我们仍然是用权值和来举例子,对于J->L这一条链上所有元素的和,我们本来应该把JGEBACFHL的权值全部加起来,但是你的计算机并没有那么牛X的空间想象能力,所以需要我们做一些处理,如果你仔细观察就可以轻松发现,J+G+E+B+A+C+F+H+L,假设我们用dis[N]这个数组来保存根节点到N的距离(很类似spfa之类的求最短路径的算法,在dfs里就可以实现),那么节点A到节点B之间链的长度和就应该为dis[A]+dis[B]-2*dis[A、B的最近公共祖先(lca)],而dis的计算可以就放在dfs序的函数内部,用以上的函数名,两点间的边权(比如说A的点权是W【A】,B的点权是W【B】,那么我们在建立邻链表的时候,就把A->B的边权赋值成B的点权我【B】,B->A的边权则赋成A的点权W【A】),那么代码的实现其实就只需要多一句话
void dfs(int u,int f)
{
//前面的操作一模一样
for(int i=head[u];i;i=edge[i].nxt)
{
int v=edge[i].to;
if(v==f) continue;
dis[v]=dis[u]+edge[i].dis;//多的这句话就在这里啦
dfs(v,u);
}
//后面的操作也一样啦,自己看着前面的照搬吧
} 这样的话,在不涉及修改的情况之下,可以一定程度上的解决第四条和第五条的问题。当然,太复杂的问题仍然是解决不了的,因为一旦涉及修改操作,就意味着你需要重新计算dis,这样的时间花费是正常的考试根本承受不了的。
那么说了这么多,我们来总结一下以上的文章内容到底都讲了一些什么东西吧。
首先是dfs序在点、子树的修改和查询中的作用(这一套的代码实现就在上文当中)
然后是lca的定义以及它在各种情况之下的应用方法。
最后是不涉及修改操作的简单链查询。
以上。
总结一下,第三条其实不是非常的重要,要问为什么的话,你在学了树链剖分以后是不会再使用这种方法的。(这种方法不仅复杂,而且易错),所以重中之重就是一二点的内容,所以我们接下来来对lca的代码实现和具体的操作思路来做一下详细阐述
那么如何寻找lca呢?
我们首先需要知道要找到lca最少需要哪些条件。
首先是最早的dfs内部的所有条件都是根据题目来的(所以在这里我们不用管它,就在最早的seq[]的方式上做调整好了)
然后就是多出来的两个数组,father[]和dep[],father用来计算当前的节点的父亲节点,dep则用来计算它们的深度,那么father个dep的建立仍然是在dfs中就可以完成的
void dfs(int u,int f)
{
seq[++idc]=tree[u];
in[u]=idc;
for(int i=head[u];i;i=edge[i].nxt)
{
int v=edge[i].to;
if(v==f) continue;
dep[v]=dep[u]+1;//(所有树的基本性质)
father[v]=u;//我觉得这个并不需要我来解释
dfs(v,u);
}
out[u]=idc;
}那么在这个基础之上,我们要对这一套结构找lca就是这样的
void lca(int u,int v) //寻找u、v两个节点的最近公共祖先
{
while(u!=v)
{
if(dep[u]<dep[v])//这是最简单的最不用动脑子的方式,就是把更深的节点一步一步往上跳
swap(u,v);
u=fat[u];
}
return u;
}嗯,非常简单,当然,出题人要卡你更简单,这样的话,找个lca都要O(n)的复杂度,更不要提题目里还有其他操作了。
所以我们可以用二进制优化的方式,来把查找lca的复杂度优化到达O(log(n))(注意这是最常见也是最基础的方法,但是需要用到一些二进制的知识,如果说不会的话请先去学习一下位运算的二进制计算方式,当然我以后也会在博客上慢慢地把这些坑都填上。。。。位运算应该也会讲吧,还有,正常情况下,会线段树和树状数组的人应该都是知道位运算怎么用的吧。。)
那么我们需要对于dfs的函数里做一些改动,因为我们在这里除了数组dep[]和数组fat[]之外,还增加了anc[][]这个最重要的数组;
1、anc[u][p] 最最最最最最重要的一个数组,它所代表的含义是u这个节点往上跳2^p层后所对应的节点,注意这里的p是可以为零的(向上跳2^0层,也就是向上跳一层),所以在写代码的时候,请务必记住将anc[u][0]赋上初值。
我们要明白我们这套优化的基本思路跟刚才那套是很类似的,但是我们是采用双点一起跳的方案,而且用2^n的步数来往上跳,这样的话就可以使得寻找节点的时间复杂度变得非常的短(注意,这里使用2^n不会对结果产生影响,由于二进制本身的特性,使得每一个数都是可以用二进制来表示的,比如7可以分解成为2^2+2^1+2^0),所以说用2^n来表示节点是不会跳过或者是跳不到的(这个具体会涉及到很多内容,因为二进制的有些东西是有固有性质的,希望以后我有时间来填坑)。
那么最终版本的dfs代码实现如下
#include<bits/stdc++.h>
using namespace std;
const int P=15+6;
const int MAXN=1e5+5;
int anc[MAXN][P+1];
void dfs(int u,int f)
{
anc[u][0]=f;//由于f是u的父亲节点,所以说u向上跳一层的位置就是f,因此anc[u][0]就是f
for(int p=0;p<=P;p++)//这事一个非常easy的递推式子,只要有一点计算机的基础就可以轻松推出来,但是要详细阐述实在是太花时间了,实在不行的话请读者亲身验证一下。
{//傲!对了,请大家注意一下上面P的定义,我在这里的anc[][]定义到了P+1,所以说循环的时候是p<=P,如果说是定义的P的话,循环的时候只能是p<P哟
anc[u][p]=anc[anc[u][p-1]][p-1];
}
for(int i=head[u];i;i=edge[i].nxt)//标准的dfs序内部结构
{
int v=edge[i].nxt;
if(v==u) continue;
dep[v]=dep[u]+1;
fat[v]=u;
dfs(v,u);
}
}以上是基本操作,也就是说把anc等各个数组的条件全部都赋上去了。这个部分还算比较简单,但是接下来寻找lca的过程也许会让人一脸懵逼。(由于要知道的东西太多,所以我就不再程序里加上注释了,直接在此做解释)
首先我们要知道位运算操作符的>>和&的含义。
A>>n是指把一个数A(二进制状态)所有的位置向右移动n位,用数学的角度上来说就是把这整个数字A除以2^n(但是最终是要取整的,因为本身就定义是整形常量具有的性质),具体过程大概如下。
首先我们要明白二进制转化成十进制的方法,就拿1101来说,从右往左数(注意我们是从0开始数的),第0位是1,第1位是0,第二位是1,第三位是1,所以1101=1*2^0+0*2^1+1*2^2,结果是13.
我们把13表示成二进制,是1101,所以说向右平移一位过后,最后一位消失,然后变成了110,也就是0*2^0+1*2^1+1*2^2,也就是6,正好对应13/2的在整形变量除法的时候对应的结果,所以说13>>1=6(读者们都注意一下,当多个位运算操作符号同时要使用的时候,请记住,绝对要打括号,不管你的顺序是不是正确的,总之打上括号就好了,因为位运算操作符的运算顺序实在是太扯淡了)。
而&是按位与,当设C=A&B(A、B、C均为二进制)时,A和B两个数字的某一位都是1的时候,C的对应位置也是1,否则C的对应位置为0,比如1101&1001=1001。当A的位数大于B的时候,B在前面加前缀0补齐,比如说10010111&110=10010111&00000110=110,所以说我们就可以发现一个惊(pu)人(tong)的规律,任何一个数M&1,当M的末尾是1的时候,结果是1,否则的话,结果为0,因为对于1来说,它前面的所有位数都是用0来补齐的,所以与出来都是0,只有M的末尾位数不为0的时候,才能够返回1,换句话来说,M&1可以看作是取出最后一位的1。
我们讲这些内容到底有什么用呢?用处可大了。(我相信对于二进制有感觉的读者们应该已经明白为什么anc[][])
如果我们用刚才的方法来寻找最近公共祖先的话,时间复杂度就是O(n)(每次都把深度底的那个节点往上跳),可是如果我们用这个方法的话,我们每一次是往右边移动一个位数(不要小瞧二进制可以移动的位数,对数函数的增长缓慢程度简直吓人),就可以把O(n)的时间缩短为O(log(n)),当数字非常大的时候,可以把循环次数减少好几个0。
所以在知道这些以后,我们来看一看O(log(n))的查找方式的代码实现。
void lca(int u,int v)//查找u,v的最近公共祖先lca
{
if(dep[u]<dep[v])
{
swap(u,v);
}
int t=dep[u]-dep//这是两个节点之间的层数差
for(int p=0;t;t>>=1,p++)
{
if(t&1) u=anc[u][p];//我们将较深的节点跳到较浅的位置,这里也就是刚才的应用,p每次增加的是1,意味着每一次移动的点就是2^p,所以说我们的anc要那么定义
}
if(v==u)return u;//这里是为了防止u,v中的某一个就是另一个的lca,所以当两者深度相同的时候就开始作比较,如果两个节点本身就一样的话,就意味着可以返回了
for(int p=P;p>=0;p--)
{
if(anc[u][p]!=anc[v][p])//从上而下对比,找到最后一个两者ca不一样的位置 ,然后这个位置的上方就是两者的lca。
{
u=anc[u][p];
p=anc[u][p];
}
}
return anc[u][0];
}大概的思路在注释里已经解释的很详细了,这套代码稍微有些复杂,所以说我们要搞明白具体细节的话,需要自己拿草稿纸模拟一遍。
这套方法对任意两个点的lca查询复杂度是log(n)的,所以我们就可以为所欲为啦;
当然我们还有另一种ST表(RMQ)的做法,需要nlog(n)的时间作预处理(预处理时间长于上面的那个方法),但是查询可以做到O(1)(远远低于上面那个方法),ST表的比较关键词仍然是深度,具体过程是差不多的,两个方法我推荐上面的那种。因为ST表在有一些特殊的题里会爆栈,实际上在这两种方法中,我们只需要完全掌握其中一种,并且对另一种有所了解就足够啦。
这里还是给大家贴一下ST表做法的代码实现吧(具体过程其实差不多,我也不多赘述)
void dfs(int u, int f) {
for(int t = head[u]; t; t = last[t]) {
int v = dest[t];
if(v == f) continue;
seq[++idc] = v;
pos[v] = idc;
dep[v] = dep[u] + 1;
dfs(v, u);
seq[++idc] = u;
pos[u] = idc;
}
}
void init() {
logb[0] = -1;
for(int i = 1; i < N; i++)
logb[i] = logb[i>>1] + 1;
for(int p = 0; p <= P; p++) {
for(int i = 1; i + (1<<p) - 1 <= idc; i++) {
if(p == 0) {
stu[i][p] = seq[i];
} else {
int l = stu[i][p-1], r = stu[i+(1<<(p-1))][p-1];
stu[i][p] = (dep[l] < dep[r]) ? l : r;
}
}
}
}
int lca(int u, int v) {
u = pos[u], v = pos[v];
if(u > v) swap(u,v);
int len = v - u + 1;
int p = logb[len];
int uu = stu[u][p];
int vv = stu[v - (1<<p) + 1][p];
return dep[uu] < dep[vv] ? uu : vv;
}
int main() {
idc = 0;
seq[++idc] = root;
dep[root] = 1;
dfs(root, root);
init();
}那么在今天的内容全部搞懂以后,就能够处理前5个操作啦,这也就是最基础的树形结构中的一些查询、修改操作,为了搞定第六个操作,我会在这几天再写一篇有关于树链剖分的博客,用树剖可以直接解决以上的6个问题,但是我们也还是需要掌握这些基础(相信我,树链剖分很麻烦的,虽然线段树好像很长的样子,但是等到我们学了树剖以后就会发现,动脑子就可以少动手,动手就可以少动脑子。。。。所以说今天的内容和树剖都必须要掌握而且要能够看情况变通)。
所以说也祝这几天还在csdn上奋斗还顺便看到了我这个新人的拙劣博客的读者们新年快乐啦!^_^