一、概念
树状数组又称为 二叉索引树 也称作 Binary Indexed Tree,又叫做Fenwick树;
它的查询和修改的时间复杂度都是 log(n),空间复杂度则为 O(n)
这是因为树状数组通过将 线性结构转化成 树状结构,从而进行跳跃式扫
通常用下图来表示
但是这个树是怎么构建的呐?
这里就不得不感叹大牛们的脑洞之大了,竟然能想出来用二进制末尾零的个数多少来构建树的高度
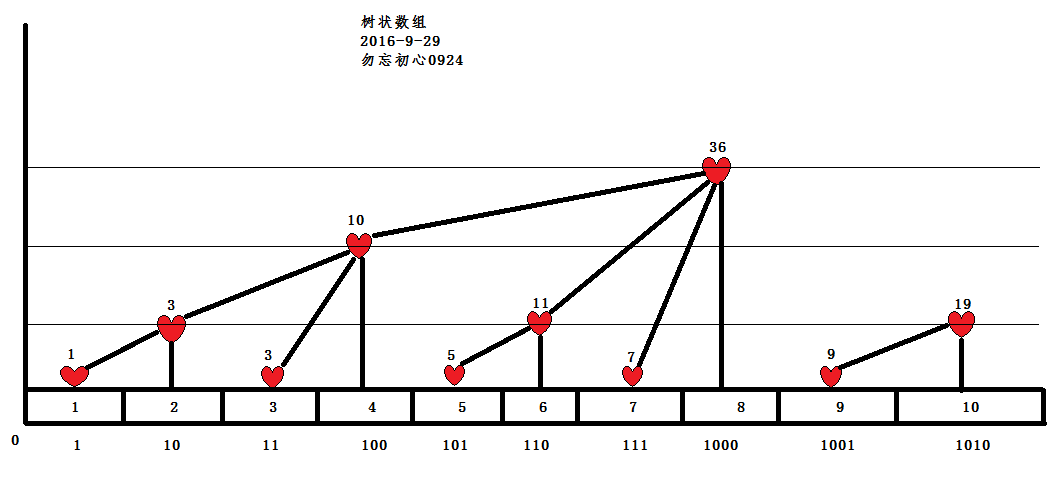

C[i]代表 子树的叶子结点的权值之和
其中 a数组就是原数组,c数组则是树状数组(也就是求和数组),可以发现
C1 = A1
C2 = A1+A2
C3 = A3
C4 = A1+A2+A3+A4
C5 = A5
C6 = A5+A6
C7 = A7
C8 = A1+A2+A3+A4+A5+A6+A7+A8公式:
C[ i ]=a[ i - 2^k+1 ] + a[ i - 2^k +2] + ...... + a[ i ] ( k = lowbit ( i ) )
得出的两点结论:
(1)、x 的父亲节点—— x + ( x & ( - x ))
(2)、x的前一个根节点—— x -( x & ( - x ))(若 x 是2的幂级数,则他的前一个根节点是 0,因为 它的 lowbit 是他本身)
二、原理及做法
首先我们搞明白树状数组是用来干嘛的,现在有一个这样的问题:有一个数组a,下标从0到n-1,现在给你w次修改,q次查询,修改的话是修改数组中某一个元素的值;查询的话是查询数组中任意一个区间的和,w + q < 500000。
朴素做法复杂度太高了,所以就有了树状数组这个算法
一般用来 区间更新 + 查询任意一个区间的和
1、lowbit() 函数
(1)、
lowbit这个函数的功能就是求某一个数的二进制表示中最低的一位1
举个例子,x = 6,它的二进制为110,那么lowbit(x)就返回2,因为最后一位1表示2
(2)、如何求 lowbit()
有两种算法:
int lowbit(x)
{
return x - (x & (x - 1));
}int lowbit(x)
{
return x & -x;
}2、求前缀和
先定义一些东西: a 是原数组,c 是新开的一个数组,这个 c 数组代表后缀和(问题模型中是用的前缀和,这里要用后缀和,具体原因马上就知道了);
二进制的视角:一个数n,假设n = 6,它的二进制为110,我们把它表示成累加的形式110 = 100 + 10,这样是可以的,那么我们要求前6(110)项的和是不是可以这样求:
C[6]=(a1+a2+a3+a4)+(a5+a6)
注意括号中的元素个数,是不是4(100) 个加 2(10) 个,和 110 = 100 + 10 是不是很像,不知你们发现了吗,10就是lowbit(110)的结果,100是lowbit(100) 的结果。求和的时候我们总是把求和区间拆分成这样的几段区间和来计算,而如何去确定这些区间的起点和长度呢?
就是根据n的二进制来的(不懂的可以再看下上面举的例子),二进制怎么拆的,你就怎么拆分,而拆分二进制就要用到上面说的lowbit函数了。
这里也可以顺理成章得给出c数组的表示了,c[i]表示从第i个元素向前 数 lowbit(i) 个元素,这一段的和,这就是上面说的区间和,只不过这个区间是靠右端点的;你可能又会想,不是说区间是靠右端点的吗,是后缀和啊,那中间的这些区间怎么定义?其实递归定义就好了,
比如说求前6项的和
∑=(a1+a2+a3+a4)+(a5+a6)=∑(a1+a2+a3+a4)+c[6],
你把c[6]去掉,不就是前四项和 ∑=(a1+a2+a3+a4)
这个区间不就靠右端点了吗, 前四项和 ∑=c[4]= c[6−lowbit(6)]
三、CODE
1、若求 区间 [ x , y ] 的和,则用 Getsum(y)-Getsum(x-1)
2、
单点更新:
此时如果我们要更改A[1]
则有以下需要进行同步更新
1(001) C[1]+=A[1]
lowbit(1)=001 1+lowbit(1)=2(010) C[2]+=A[1]
lowbit(2)=010 2+lowbit(2)=4(100) C[4]+=A[1]
lowbit(4)=100 4+lowbit(4)=8(1000) C[8]+=A[1]
3、
区间查询,求和:
举个例子 i=5
C[4]=A[1]+A[2]+A[3]+A[4];
C[5]=A[5];
可以推出: sum(i = 5) ==> C[4]+C[5];
序号写为二进制: sum(101)=C[(100)]+C[(101)];
第一次101, 减去最低位的1就是100;
其实也就是单点更新的逆操作
树状数组更新与求和分为两种
区别:
看具体题目,适合哪一种
1、向上更新向下求和
int Getsum(int i) // 向下求前缀和
{
int ans=0;
while(i)
{
ans+=c[i];
i-=lowbit(i);
}
return ans;
}
void update(int i,int v) // 向上单点更新,加上包含它的区间
{
while(i<=n)
{
c[i]+=v;
i+=lowbit(i);
}
}
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
update(i,a[i]);
}2、向下更新向上求和
int getSum(int num) //向上统计每个区间和
{
int sum=0;
while(num<=n)
{
sum+=c[num];
num+=lowbit(num);
}
return sum;
}
void update(int num,int val) //向下更新,num是要更新的子节点,val是要修改的值
{
while(num>0)
{
c[num]+=val;
num-=lowbit(num);
}
}
四、求逆序对
什么是逆序对?
——
设 A 为一个有 n 个数字的有序集 (n>1),其中所有数字各不相同。
如果存在正整数 i, j 使得 1 ≤ i < j ≤ n 而且 A[i] > A[j],则 <A[i], A[j]> 这个有序对称为 A 的一个逆序对,也称作逆序数
对于一个包含N个非负整数的数组A[1..n],如果有i < j,且A[ i ]>A[ j ],则称(A[ i] ,A[ j] )为数组A中的一个逆序对。
例如,数组(3,1,4,5,2)的逆序对有(3,1),(3,2),(4,2),(5,2),共4个
思路:
用树状数组来做
有需要离散化的,先进行离散化
离散化前几篇博客有详解
离散化代码
for(int i=1; i<=n; i++)
{
scanf("%d",&s[i].x);
s[i].order=i;
}
sort(s+1,s+n+1,cmp);
for(int i=1; i<=n; i++)
dis[s[i].order]=i;求逆序对核心CODE
for(int i=1; i<=n; i++)
{
Update(dis[i],1);
ans+=i-Getsum(dis[i]);
}解释代码:
Getsum:求得是dis [ i ] 前边比 dis [ i ] 小的数字的个数
i:代表的是 插入了几个数
i - Getsum() :dis [ i ] 前边比 dis [ i ] 大的数字有几个,满足逆序对的定义
我们假设一个数组A[n],当A[n]=0时表示数字n在序列中没有出现过,A[n]=1表示数字n在序列中出现过。A对应的树状数组为c[n],则c[n]对应维护的是数组A[n]的内容,即树状数组c可用于求A中某个区间的值的和。
介绍 Getsum 函数:
该函数的作用是用于求序列中小于等于数字 i 的元素的个数。
这个是显而易见的,因为树状数组c 维护的是数组A的值,则该求和函数即是用于求下标小于等于 i 的数组A的和,而数组A中元素的值要么是0要么是1,所以最后求出来的就是小于等于i的元素的个数。