一 什么是树状数组?
我们先来看一道题:
例题1(单点修改区间查询):已知N个正整数,接下来我们对这N个数进行M次操作,这M次操作可能是:
①将第X个数加上V ②询问区间[P1,P2]的和。
如果不知道树状数组的话,我们可以选择暴力的选择:
每次进行①时,就将第X个数加上V;
每次进行②时,就for一次求出[P1,P2]的和。
我们来计算出它的时间复杂度为O(M*N)。
为什么这么复杂?因为每次改一个数,就会影响众多的区间。
接着我们选择了前缀和:
求出所有的前缀和,每次加上V后,把第X后面的所有前缀和都加V。
貌似时间复杂度好像还是MN呐……
那怎么办呢?我们需要一个数组,既可以求出前缀和,长度还能尽量小。
定义一个数组c(a是原数组)
c[i]=a[i]+a[i-1]......+a[i – 2^k + 1](其中k是最大的自然数使2^k是i的因数)
c[i]数组大概是这样的:
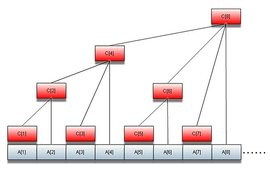
如果我们想求S[6],只需要用c[6]+c[4]即可
如果我们需要S[7],只需要用c[7]+c[6]+c[4]即可。
而且c数组的长度为log2(N),所以时间复杂度只有O(log2(N))
而这个c数组,就是我们所称的树状数组。
二 建立树状数组
1、找规律
我们针对两个例子,来看看如何维护c数组。
例子1:将a数组的第7个数+2
我们可以发现:我们需要将c[7],c[8],c[16]......加上2。
例子2:将a数组的第5个数+19
我们可以发现:我们需要将c[5],c[6],c[8],c[16]......加上19。
我们观察这两组数:7 8 16 ||| 5 6 8 16
他们两两之差是:1 8 ||| 1 2 8
恰好和上面k的性质相同:其差恰好为最大满足2^k是前面那个数的因数的自然数!
我们只需要将这个2^k求出来,运用函数的知识求出来就可以了!
定义函数lowbit
int lowbit(int x){
return x&(-x);
}
为什么是x&(-x)?
由于计算机是用二进制工作的,我们举一个二进制的例子:
x=10001100
-x=01110011+1=01110100
x&(-x)=00000100
我么就可以求出2^k=(100)2=4
把(10001100)2 转化为10进制,是32+8+4=44
因此,我们可以用lowbit求出2^k。
2、第①个操作——加V
这一次我们献上代码:
void fa(int x,int v){
while(x<=n)
{
c[x]+=v;
x+=lowbit(x);
}
}
这就是我们上面找的规律,是不是很简单?
3、查询query
这里的query其实指的是求前缀和,到时候我们需要用前缀和(q)-前缀和(p-1)
求前缀和的时候,这个关于k的规律展现出耀眼的光芒:
举一个栗子:

x=7时 我们要将c[7],c[6],c[4]加起来,7,6,4,的确满足那个规律!
因此我们还要用一次lowbit
int query(int p){
int sam;
sam=0;
while(x)
{
sam+=c[x];
x-=lowbit(x);
}
return sam;
}
三、主函数
int x,p,q,r,s;
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>a[i];
c[i]+=a[i];
if(i+lowbit(i)<=n)
c[i+lowbit(i)]+=c[i];
}
cin>>m;
for(int i=1;i<=m;i++)
{
cin>>x;
if(x==1)
{
cin>>p>>q;
fa(p,q);
}
if(x==2)
{
cin>>p>>q;
cout<<query(q)-query(p-1)<<endl;
}
}
return 0;