概述
在求解最优化问题中，拉格朗日乘子法（Lagrange Multiplier）和KKT（Karush Kuhn Tucker）条件是两种最常用的方法。在有等式约束时使用拉格朗日乘子法，在有不等约束时使用KKT条件。
我们这里提到的最优化问题通常是指对于给定的某一函数，求其在指定作用域上的全局最小值(因为最小值与最大值可以很容易转化，即最大值问题可以转化成最小值问题)。提到KKT条件一般会附带的提一下拉格朗日乘子。对学过高等数学的人来说比较拉格朗日乘子应该会有些印象。二者均是求解最优化问题的方法，不同之处在于应用的情形不同。
（1）无约束条件
这是最简单的情况，解决方法通常是函数对变量求导，令求导函数等于0的点可能是极值点。将结果带回原函数进行验证即可。
拉格朗日乘子法实例
（2）等式约束条件
设目标函数为f(x)，约束条件为h_k(x)，形如:
s.t. 表示subject to ，“受限于”的意思，l表示有l个约束条件。
则解决方法是消元法或者拉格朗日法。消元法比较简单不在赘述，这里主要讲拉格朗日法，因为后面提到的KKT条件是对拉格朗日乘子法的一种泛化。
例如给定椭球:
求这个椭球的内接长方体的最大体积。这个问题实际上就是条件极值问题，即在条件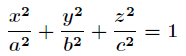 
下，求
的最大值。
当然这个问题实际可以先根据条件消去 z (消元法)，然后带入转化为无条件极值问题来处理。但是有时候这样做很困难，甚至是做不到的，这时候就需要用拉格朗日乘数法了。
首先定义拉格朗日函数F(x)：
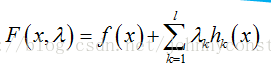
然后解变量的偏导方程：
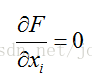
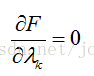
如果有l个约束条件，就应该有l+1个方程。求出的方程组的解就可能是最优化值（高等数学中提到的极值），将结果带回原方程验证就可得到解。
回到上面的题目，通过拉格朗日乘数法将问题转化为
对
求偏导得到
联立前面三个方程得到
和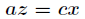
，带入第四个方程解之
带入解得最大体积为：
为什么这么做可以求解最优化
举个例子：
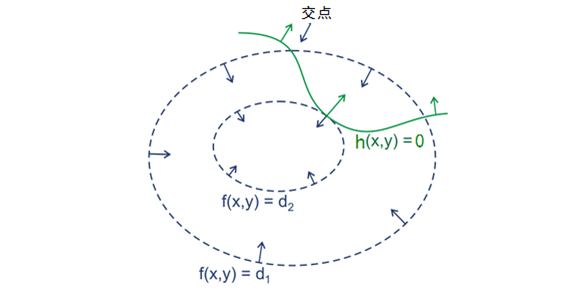
拉格朗日乘子法的几何认识
现在，我们来感性地认识一下，为什么拉格朗日认为相切才能找到最低点（只是感性认识，不添加任何数学推导）。
在橙点这个位置，由于两条曲线不相切，所以橙线的梯度（上图橙色箭头）和蓝线的切线（蓝色虚线）肯定不垂直。在这种情况下，蓝线的两个切线方向，必定有一个往函数高处走（与梯度的夹角小于 90 度），有一个往函数低处走（与梯度的夹角大于 90 度）。所以，在两条曲线相交时，我们肯定不在最低点或最高点的位置。
那么，反过来想，如果两条曲线相切（上图），那么在切点这个位置，蓝线的切线和橙线的梯度是垂直的，这个时候，蓝线的切线方向都指向橙线的等高线方向。换句话说，在切点的位置沿蓝线移动很小的一步，都相当于在橙线的等高线上移动，这个时候，可以认为函数值已经趋于稳定了。所以，我们认为这个点的值“可能”是最低（高）的（之后解释为什么是“可能“。另外，个人觉得拉格朗日乘子法最好用反证法从不相切的点入手思考，从相切的点思考总有点别扭）
根据拉格朗日乘子法的定义，这是一种寻找极值的策略，换句话说，该方法并不能保证找到的一定是最低点或者最高点。事实上，它只是一种寻找极值点的过程，而且，拉格朗日乘子法找到的切点可能不只一个（也就是上面的方程组可能找到多个解），例如下图：
图中相切的点有两个，而红点的函数值明显比黑点小。事实上，要想判断找到的点是极低点还是极高点，我们需要将切点代入原函数再进行判断。
很简单例子1
虽然上面已经有一个实例的例子了，但总感觉有点乱，原理啥的也不是让人特别清晰。所以接下来会再举一个便于理解的例子。
求此方程的最大值：
s.t
因为只有一个未知数的限制条件，我们只需要用一个乘数λ.
将所有L方程的偏微分设为零，得到一个方程组，最大值是以下方程组的解中的一个：
由上面三个条件可以知道，取到最优解时，必然满足等式约束。
解得
实际上这边没必要对求偏导，求了也就是原来的等式约束。
很简单例子2
又看到一个例子，mark一下，希望能帮助理解。
这边为什么没有对求导呢？注意看，有一句话“把它在带到约束条件中去”，其实就是对
求导了，因为f对
求导之后就是约束条件。
系数λ的作用
这边的λ和上面的一样的。
对于有不等式约束的问题我们要引进KKT条件和对偶变换。在下一篇中会详细介绍。
参考文章：