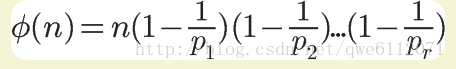加密概要
加密技术是对信息进行编码和解码的技术,编码是把原来可读信息(又称明文)译成代码形式(又称密文),其逆过程就是解码(解密),加密技术的要点是加密算法,加密算法可以分为三类:
1. 对称加密
2. 非对称加密
3. 不可逆加密
对称加密算法
- 加密过程:
- 将明文分成N个组,然后对各个组进行加密,形成各自的密文,最后把所有的分组密文进行合并,形成最终的密文。
- 优点:
- 算法公开、计算量小、加密速度快、加密效率高
- 缺点:
- 交易双方都使用同样钥匙,安全性得不到保证
- 密钥管理困难,尤其是在分布式网络中
- 常用算法:
- DES、3DES(TripleDES)、AES、RC2、RC4、RC5和Blowfish
非对称加密算法
- 使用过程:
- 乙方生成两把密钥(公钥和私钥)
- 甲方获取乙方的公钥,然后用它对信息加密。
- 乙方得到加密后的信息,用私钥解密,乙方也可用私钥加密字符串
- 甲方获取乙方私钥加密数据,用公钥解密
- 优点:
- 更安全,密钥越长,它就越难破解
- 缺点:
- 加密速度慢
- 常用算法:
- RSA、Elgamal、背包算法、Rabin、D-H、ECC(椭圆曲线加密算法)
RSA算法历史
1977年,三位数学家Rivest、Shamir 和 Adleman 设计了一种算法,可以实现非对称加密。这种算法用他们三个人的名字命名
数论基础
1. 欧拉函数
- 定义:对于一个正整数 n ,小于 n 且和 n 互质的正整数(包括 1)的个数,记作 φ(n).则
- 证明:
- 如果n是一个质数,那么
φ(n) = n-1 - 如果n是一个质数p的幂,即
n = p^k,则φ(n) = p^k-p^(k-1) = (p-1)*p^(k-1) - 欧拉函数是一个积性函数,当n,m互质的时候,
φ(n*m) = φ(n)*φ(m)
- 如果n是一个质数,那么
2. 欧拉定理
- 定义:如果两个正整数a和n互质,则n的欧拉函数 φ(n) 可以让下面的等式成立:a^φ(n)%n=1
- 证明:
3. 费马小定理
- 定义:假设正整数a与质数p互质,因为质数p的φ(p)等于p-1,则欧拉定理可以写成:a^(p-1)%n=1
4. 模反元素(乘积逆元)
- 定义:两个正整数a和n互质,那么一定可以找到整数b,使得 ab-1 被n整除,或者说ab被n除的余数是1:a*b%n=1,这时,b就叫做a的”模反元素”。
- 比如,3和11互质,那么3的模反元素就是4,因为 (3 * 4)-1 可以被11整除。4加减11的整数倍都是3的模反元素 {…,-18,-7,4,15,26,…},即如果b是a的模反元素,则 b+kn 都是a的模反元素
- 模反元素必定存在,因为:
a^φ(n)=a*a^(φ(n)-1)
RSA算法实现步骤
- 原理:将两个大素数相乘十分容易,但是想要对其乘积进行因式分解却极其困难,因此可以将乘积公开作为加密密钥
- 下面是产生非对称密钥的算法流程
-
下面是加解密的算法流程
-
RSA算法可靠性分析
- 算法涉及到的参量:p、q、n、Φ(n)、e、d,而d泄露->私钥被破解,问题:能否在已知n和e的情况下,推导出d?
- 破解步骤:
- ed≡1 (mod φ(n))。只有知道e和φ(n),才能算出d。
- φ(n)=(p-1)(q-1)。只有知道p和q,才能算出φ(n)。
- n=pq。只有将n因数分解,才能算出p和q。
- 需要将因式分解n,当n位数达到1024,破解极为困难
RSA核心算法
快速幂取模算法
- 算法1:连乘算法,时间复杂度O(n)
- 算法2:快速幂算法,时间复杂度O(logn)
def myPow(self, x, n):
def rec_pow(x,n):
if n == 0:
return 1
elif n == 1:
return x
return rec_pow(x*x,n / 2) * rec_pow(x,n&1)
if n >= 0:
return rec_pow(x,n)
else:
return 1/rec_pow(x,-n)- 算法3:快速幂取模算法,时间复杂度O(logn)
def superPow(self, a, b,m):
def myPow(a,b):
if b == 0:
return 1
a = a%m
if b == 1:
return a
return myPow(a*a,b/2) * myPow(a,b&1) % m
res = myPow(a,b)
return res素数判定算法
- 算法1:试除法,错误率=0,时间复杂度o(n),当数特别大时,算法速度慢
- 算法2:费马小定理
- 出错分析:
- 若基于2为底,对于512位大数,出错率为1/1020
- 卡米歇尔(Carmichael)数:它是合数, 当 1<=a<=n, 都有 a^n 三 a(mod n),255/100,000,000
- 卡米歇尔数的考塞特判别法: 设n是合数,则n是卡米歇尔数当且仅当它是奇数,且整除n的每个素数p满足下述两个条件:
- p^2 不整除 n
- p-1 整除 n-1
- 出错分析:
- 算法3:米勒拉宾素数测试
- 随机选取多组基数
- 改进:如果p是一个奇素数,方程x2≡1(mod p)仅仅有-1、1两个平凡解
- 速度快,而且可以判断
<2^63的数 - 合数的拉宾-米勒测试定理: 设n是奇素数, 记
n-1 = 2^k * q, q 是奇数, 对不被n整除的某个a, 如果下述两个条件都成立,则n是合数.a^q !三 1(mod n);- 对所有 i = 0, 1, 2, …., k-1,
a^((2^i)*q) !三 -1(mod n);
根据以上定理,可设计如下素数判定算法:
## 以一定概率判断是否为素数
def primeTest(n):
q = n - 1
k = 0
#Find k, q, satisfied 2^k * q = n - 1
while q % 2 == 0:
k += 1;
q /= 2
a = random.randint(2, n-2);
#If a^q mod n= 1, n maybe is a prime number
if fastExpMod(a, q, n) == 1:
return True
#If there exists j satisfy a ^ ((2 ^ j) * q) mod n == n-1,
#n maybe is a prime number
for j in range(0, k):
if fastExpMod(a, (2**j)*q, n) == n - 1:
return True
#a is not a prime number
return False
#多次测试,知道获取基本不可能为素数的“奇数”
def findPrime(halfkeyLength):
while True:
#Select a random number n
n = random.randint(0, 1<<halfkeyLength)
if n % 2 != 0:
found = True
#If n satisfy primeTest 10 times, then n should be a prime number
for _ in range(0, 10):
if not primeTest(n):
found = False
break
if found:
return n拓展欧几里德算法
- 欧几里德算法(辗转相除法)
a=bq1+r1
b=rq2+r2
r1=r2q3+r3
……
rk-2=rk-1qk+rk
rk = 0,rk-1=gcd(a,b)
如gcd(20,7)=gcd(7,6)=gcd(1,0)
def gcd(a,b):
if not b:
return a
return gcd(b,a%b)- 拓展的欧几里得算法:ax+by=rk-1=gcd(a,b),求一组x,y
- 求逆元d:ed mod (p-1)*(q-1) = 1 =>
- 设 m = (p-1)*(q-1),则mk+ed=1=gcd(m,e)
- 求满足条件的一组解k,d,最后取d
def ex_gcd(a,b):
global x,y
x,y = 1,0
def ex_gcd2(a,b):
global x,y
if b == 0:
return a
t = ex_gcd2(b, a%b)
x,y = y,x-(a/b)*y
return t
return ex_gcd2(a,b),x,yRSA实际应用
SSH安全验证
- 级别一:基于口令
- /etc/ssh/ssh_known_hosts
- 级别二:基于公钥(安全通信)
- ~/.ssh/id_rsa.pub
- ~/.ssh/id_rsa
- ~/.ssh/authorized_keys
数字签名&https原理
- 摘要算法(Hash算法、散列算法)
- 特性:
- 长度固定
- CRC32 32比特(4字节)
- MD5 128比特(16字节)
- SHA1 160比特(20字节)
- 不可逆性
- 确定性
- 长度固定
- 应用:完整性校验
- 校验文件是否缺失、被破坏、被修改
- 特性:
- 数字证书
- 具体内容
- 证书的发布机构
- 证书的有效期
- 公钥,证书所有者的公钥
- 证书所有者(Subject)
- 签名所使用的算法
- 指纹以及指纹算法,用于校验证书合法性
- 数字证书可以保证数字证书里的公钥确实是这个证书的所有者
- 具体内容