[NOI2018 D1T1]归程【Kruskal重构树】

时空限制 4000ms / 512MB

题目描述

本题的故事发生在魔力之都，在这里我们将为你介绍一些必要的设定。魔力之都可以抽象成一个 $n$ 个节点、 $m$ 条边的无向连通图（节点的编号从 $1$ 至 $n$ ）。我们依次用 $l,a$ 描述一条边的长度、海拔。作为季风气候的代表城市，魔力之都时常有雨水相伴，因此道路积水总是不可避免的。由于整个城市的排水系统连通，因此有积水的边一定是海拔相对最低的一些边。我们用水位线来描述降雨的程度，它的意义是：所有海拔不超过水位线的边都是有积水的。

Yazid 是一名来自魔力之都的OIer，刚参加完ION2018 的他将踏上归程，回到他温暖的家。 Yazid 的家恰好在魔力之都的 $1$ 号节点。对于接下来 $Q$ 天，每一天Yazid 都会告诉你他的出发点 $v$ ，以及当天的水位线 $p$ 。每一天，Yazid 在出发点都拥有一辆车。这辆车由于一些故障不能经过有积水的边。 Yazid 可以在任意节点下车，这样接下来他就可以步行经过有积水的边。但车会被留在他下车的节点并不会再被使用。需要特殊说明的是，第二天车会被重置，这意味着：

车会在新的出发点被准备好。
Yazid 不能利用之前在某处停放的车。 Yazid 非常讨厌在雨天步行，因此他希望在完成回家这一目标的同时，最小化他步行经过的边的总长度。请你帮助 Yazid 进行计算。本题的部分测试点将强制在线，具体细节请见【输入格式】和【子任务】。

输入格式：

单个测试点中包含多组数据。输入的第一行为一个非负整数 $T$ ，表示数据的组数。

接下来依次描述每组数据，对于每组数据：

第一行 $2$ 个非负整数 $n,m$ 分别表示节点数、边数。

接下来 $m$ 行，每行 $4$ 个正整数 $u, v, l, a$ 描述一条连接节点 $u, v$ 的长度为 $l$ 、海拔为 $a$ 的边。在这里，我们保证 $1 \leq u,v \leq n$

接下来一行 $3$ 个非负数 $Q, K, S$ 其中 $Q$ 表示总天数， $K \in {0,1}$ 是一个会在下面被用到的系数， $S$ 表示的是可能的最高水位线。

接下来 $Q$ 行依次描述每天的状况。每行 $2$ 个整数 $v_0; p_0$ 描述一天：
这一天的出发节点为 $v = (v_0 + K \times \mathrm{lastans} - 1) \bmod n + 1$
这一天的水位线为 $p = (p_0 + K \times \mathrm{lastans}) \bmod (S + 1)$
其中 lastans 表示上一天的答案（最小步行总路程）。特别地，我们规定第 $1$ 天时 lastans = 0。在这里，我们保证 $1 \leq v_0 \leq n,$ $0 \leq p_0 \leq S$

对于输入中的每一行，如果该行包含多个数，则用单个空格将它们隔开。

输出格式：

依次输出各组数据的答案。对于每组数据：
输出 $Q$ 行每行一个整数，依次表示每天的最小步行总路程。
1

说明

【样例1 解释】第一天没有降水，Yazid 可以坐车直接回到家中。

第二天、第三天、第四天的积水情况相同，均为连接1; 2 号节点的边、连接3; 4 号点的边有积水。

对于第二天，Yazid 从2 号点出发坐车只能去往3 号节点，对回家没有帮助。因此 Yazid 只能纯靠徒步回家。

对于第三天，从4 号节点出发的唯一一条边是有积水的，车也就变得无用了。Yazid只能纯靠徒步回家。

对于第四天，Yazid 可以坐车先到达2 号节点，再步行回家。

第五天所有的边都积水了，因此Yazid 只能纯靠徒步回家。

本组数据强制在线。

第一天的答案是0，因此第二天的
$v = (5 + 0 - 1) mod 5 + 1 = 5,p = (2 + 0) mod (3 + 1) = 2$
第二天的答案是2，因此第三天的
$v = (2 + 2 - 1) mod 5 + 1 = 4,p = (0 + 2) mod (3 + 1) = 2$
第三天的答案是3，因此第四天的
$v = (4 + 3 - 1) mod 5 + 1 = 2,p = (0 + 3) mod (3 + 1) = 3$

所有测试点均保证 $T \leq 3$ ，所有测试点中的所有数据均满足如下限制：

$n≤2×10 ^5, m \leq 4×10 ^5,Q \leq 4×10 ^5, K \in {0,1}, 1 \leq S \leq 10^9$
对于所有边： $l \leq 10^4,a \leq 10^9$
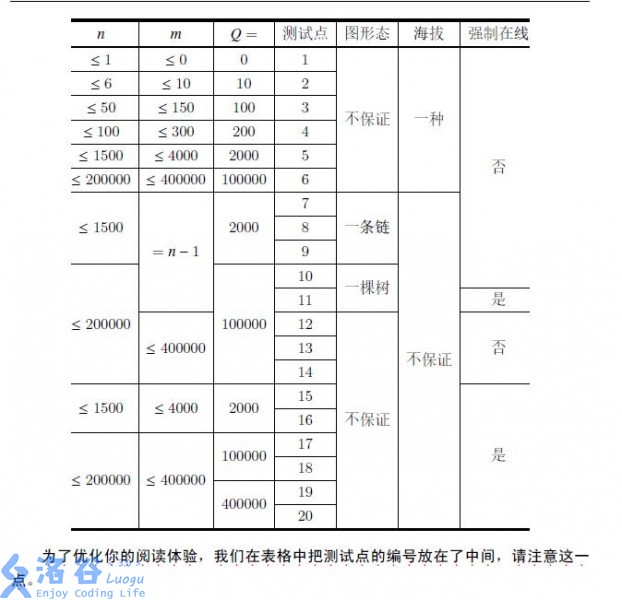
任意两点之间都直接或间接通过边相连。为了方便你快速理解，我们在表格中使用了一些简单易懂的表述。在此，我们对这些内容作形式化的说明：
图形态：对于表格中该项为“一棵树”或“一条链”的测试点，保证m = n-1。除此之外，这两类测试点分别满足如下限制：
一棵树：保证输入的图是一棵树，即保证边不会构成回路。
一条链：保证所有边满足u + 1 = v。
海拔：对于表格中该项为“一种”的测试点，保证对于所有边有a = 1。
强制在线：对于表格中该项为“是”的测试点，保证K = 1；如果该项为“否”，则有K = 0。
对于所有测试点，如果上述对应项为“不保证”，则对该项内容不作任何保证。

题目分析

蒟蒻打同步赛的时候写了个暴力只得了六十多
比赛结束后冥思苦想终于想出了正解
然而还是调了一天才调出来

咳咳，回到正题
这题正解就是Kruskal重构树

从直观思路入手
我们可以把从v到1的路径分成两部分
一半全开车，一半全走路

也就是说要枚举n个节点作为断点(假设当前断点为u)
这个断点是可行解与最优解当且仅当
存在一条从v到u的路径可以全部开车
且从u到1全部走路的最短路是满足上一条件中最短的

那么要怎么求出从v出发可以开车到的点呢
显然从v出发开车可以到的点
一定满足路径上所有边海拔都高于水位

这里已经很明显可以用Kruskal重构树求解了
我们把每条边按海拔降序排序
重构树完成后
对于每次询问
找到树中深度最小且海拔大于水位的节点
那么他的子树的全部节点都可以由v开车到达

这一点可以由重构树是小根堆的性质简单得证
即每个节点子树内所有节点海拔都比该节点大

而求解这个深度最小且海拔大于水位的节点可以用树上倍增，两行解决

现在要求的最后一步就是这个子树内所有节点到1号节点的步行最短路
因为是无向图，所以一开始预处理1节点到所有节点最短路就好
然后dfs可以顺便求出某个节点子树内的最短路

#include<iostream>
#include<cmath>
#include<algorithm>
#include<queue>
#include<cstring>
#include<cstdio>
using namespace std;
typedef long long lt;

lt read()
{
    lt f=1,x=0;
    char ss=getchar();
    while(ss<'0'||ss>'9'){if(ss=='-')f=-1;ss=getchar();}
    while(ss>='0'&&ss<='9'){x=x*10+ss-'0';ss=getchar();}
    return f*x;
}


const int maxn=800010;
int n,m,cnt;
lt Q,K,S;

struct node{int u, v;lt hi;}edge[maxn<<1];
bool cmp(node a,node b){return a.hi>b.hi;}

struct node2{int v,nxt;lt dis;}E[maxn<<1];
int head[maxn],tot;

lt d[maxn],vis[maxn],ff[maxn];
priority_queue< pair<lt,int> > q;

lt mi[maxn],val[maxn];
int gra[maxn][23];

void add(int u,int v,lt dis)
{
    E[++tot].nxt=head[u];
    E[tot].v=v; E[tot].dis=dis;
    head[u]=tot;
}

void dij()
{
    memset(vis,0,sizeof(vis));
    memset(d,111,sizeof(d)); d[1]=0;
    q.push(make_pair(0,1));

    while(!q.empty())
    {
        int u=q.top().second; q.pop();
        if(vis[u]) continue;

        vis[u]=1;
        for(int i=head[u];i;i=E[i].nxt)
        {
            int v=E[i].v;
            if(d[u]+E[i].dis<d[v])
            {
                d[v]=d[u]+E[i].dis;
                q.push(make_pair(-d[v],v));
            }
        }
    }
}

int find(int x)
{
    if(x==ff[x])return x;
    else return ff[x]=find(ff[x]);
}

void dfs(int u) 
{
    mi[u]=d[u];
    for(int i=head[u];i;i=E[i].nxt)
    {
        int v=E[i].v;
        gra[v][0]=u;
        dfs(v);
        mi[u]=min(mi[u],mi[v]);
    }
    //if(u<=n) 
}

void kruskal()
{
    memset(head,0,sizeof(head)); tot=1;
    sort(edge+1,edge+1+m,cmp);
    for(int i=1;i<=n;++i)ff[i]=i; 
    for(int i=1;i<=m;i++) 
    {
        int fu=find(edge[i].u), fv=find(edge[i].v);
        if(fu!=fv)
        {
            val[++cnt]=edge[i].hi;
            ff[fu]=ff[fv]=ff[cnt]=cnt;
            add(cnt,fu,0); add(cnt,fv,0);
        }
    }
    dfs(cnt);
}

void init()
{
    memset(head,0,sizeof(head)); tot=1;
    memset(gra,0,sizeof(gra)); 
    memset(mi,111,sizeof(mi));
}

int main() 
{
    int T=read();
    while(T--) 
    {
        init();
        n=read();m=read();cnt=n;

        for(int i=1;i<=m;i++)
        {
            int u=read(),v=read(),dis=read(),hi=read();
            add(u,v,dis); add(v,u,dis);
            edge[i].u=u; edge[i].v=v; edge[i].hi=hi;
        }
        dij();//预处理1到所有节点最短路
        kruskal();//重构树

        for(int i=1;(1<<i)<=cnt;i++)
        for(int u=1;u<=cnt;u++)
        gra[u][i]=gra[gra[u][i-1]][i-1];

        Q=read();K=read();S=read();
        lt last=0;
        while(Q--) 
        {
            int vi=read(),pi=read();
            vi=(vi+K*last-1)%n+1;
            pi=(pi+K*last)%(S+1);

            for(int j=22;j>=0;--j)//找到深度最小且海拔大于水位的节点
            if(gra[vi][j]&&val[gra[vi][j]]>pi) 
            vi=gra[vi][j];

            printf("%lld\n",last=mi[vi]);
        }
    }
    return 0;
}