SVM for Clustering

A Support Vector Method for Clustering

原文地址：A Support Vector Method for Clustering

本文介绍了一种基于SVM的聚类方法，核心思想是用高斯核的SVM找到多个能够包围数据的半径最小的超球。使用此方法不用预先确定类别的结构和个数。

Abstract

聚类问题可以用参数化或非参数化的方法处理。参数化方法往往限制于其表达能力（expressive power），即需要预先猜想类别的结构（概率分布）。这篇文章提出一种非参数化的基于SV的方法用来描述高维分布的特性，首先找到一个最小半径的能够包围所有数据的超球，通过减小高斯核的方差（the width parameter of the Gaussian kernel function），可以使超球分类成很多的小部分，每一小部分中包含的点便是一种类别。用软间隔解决异常值问题从而处理不同类别重叠的问题。

Describing Cluster Boundaries with Support Vectors

共有$N$个数据点$\{x_i\} \subseteq \chi$，$\chi \subseteq \mathbb{R}^d$，$\Phi$是$\chi$变换至高维的特征，加入松弛变量$\xi _j$，要想求得包围所有数据的最小半径的超球，可用下面的问题描述：

$$min~R^2+C\Sigma \xi _j \\ s.t.~\left \| \Phi {(x_j)-a} \right \|^2\leq R^2+ \xi _j, \\ \xi _j\geq 0,\forall j$$

其中$R$为半径，$a$为超求的球心，拉格朗日函数：

$$L=R^2-\Sigma(R^2+\xi _j-\left \| \Phi {(x_j)-a} \right \|^2) \beta_j- \Sigma \xi _j \mu_j+C\Sigma \xi _j,$$

其中拉格朗日乘子$\beta_j \geq0 ,\mu_j \geq 0$，$C$为惩罚参数。对$R,a,\xi_j$分别求偏导并置零得：

$$\Sigma \beta _j=1,\\a=\Sigma \beta _j\Phi(x_j),\\ \beta _j=C-\mu_j$$

KKT条件：

$$\xi _j\mu_j=0,\\(R^2+\xi _j-\left \| \Phi {(x_j)-a} \right \|^2) \beta_j)=0$$

对于样本点$x_i$：

• 若$\xi _i >0$则样本点在超球外；
• 若$\xi _i =0$则样本点在超球面上或超球面内，当$\beta_i \neq0$：
  
  • 若$0<\beta_i<C$则称样本点是一个支持向量（SV）；
  • 若$\beta_i =C$则称样本点为边界支持向量（bounded SV）

接下来拉格朗日对偶函数：

$$W=\Sigma_j \Phi(x_j)^2\beta_j-\Sigma_{i,j}\beta_i\beta_j\Phi(x_i) \cdot \Phi(x_j)$$

将上述推导出的条件代入可得约束条件变为：

$$0\leq\beta_j\leq C$$

将内积运算全部换成如下的高斯核：

$$K(x_i,x_j)=e^{-q\left \| x_i-x_j \right \|^2},$$

$q$为宽度参数（width parameter，即$\frac{1}{2\sigma ^2}$），那么拉格朗日对偶函数可写为：

$$W=\Sigma_j K(x_j,x_j)\beta_j-\Sigma_{i,j}\beta_i\beta_jK(x_i,x_j)。$$

此时数据点到球心的距离：

$$R^2(x)=\left \| \Phi {(x_j)-a} \right \|^2$$

可化为：

$$R^2(x)=K(x,x)-2\Sigma_j \beta_jK(x_j,x)+\Sigma_{i,j}\beta_i\beta_jK(x_i,x_j)$$

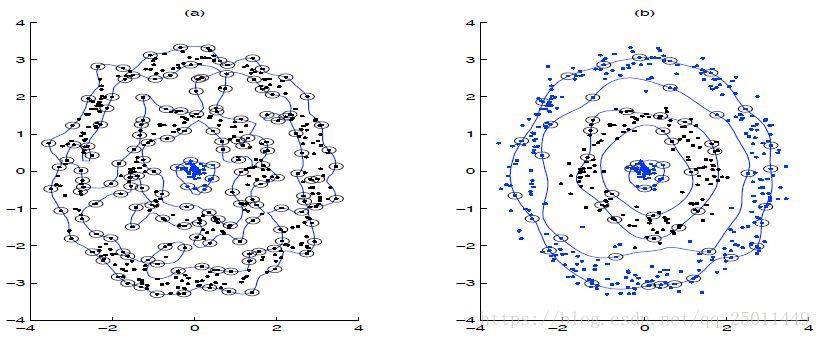
那么超球的半径即为SV到球心的距离。此时闭合轮廓的形状由参数$q$和$C$决定。如下图，$q$增大，轮廓就越贴合样本点。$q$主要定义了单个样本对整个分类超平面的影响，当$q$比较小时，单个样本对整个分类超平面的影响比较小，不容易被选择为支持向量，反之，当$q$比较大时，单个样本对整个分类超平面的影响比较大，更容易被选择为支持向量，或者说整个模型的支持向量也会多。

而当$C$减小时，如下图，轮廓边缘变得平滑，SV的数量减少，而bounded SV的数量增多（当$C<1$时bounded SV才会存在），可以更好地处理异常点。如果把惩罚系数$C$和RBF核函数的系数$q$一起看，当$C$比较大，$q$比较大时，我们会有更多的支持向量，我们的模型会比较复杂，容易过拟合一些。如果$C$比较小 ，$q$比较小时，模型会变得简单，支持向量的个数会少。

Support Vector Clustering (SVC)

为了将数据点聚类，文中介绍了一种求两点间邻接矩阵的方法：

如果两点连线间的所有点均在超球内部，说明两数据点有连接，即位于同一类。

Overlapping clusters（不是很懂）

当存在重叠时，说明bounded SV很多，SVC可以近似地看作Parzen窗概率密度估计（如下公式）。

$$p(x)=\frac {1}{N} \Sigma_iK(x_i,x)$$

Parzen窗概率密度估计值最大的点便是核心的点。

The iris data

在鸢尾花数据集的数值实验中，SVC表现要优于information theoretic approach和SPC algorithm这两个非参数化的聚类方法。具体实验结果如下：

同时，需要注意的是，SVC在低维特征上的表现要优于高维特征，因此最好事先对数据特征进行降维处理，例如PCA。

Varying $q$ and $C$

这里将如何寻找最优的$q$和$C$，对于$q$最好从小到大依次寻找，因为一个比较好的聚类通常含有较少的类别。当SV的数量超出某个范时便可确定参数$q$和$C$。