树状数组资瓷的基本操作有两个,第一个是查询前缀和,第二个是单点增加。利用差分的思想可以达到区间增加和单点查询的操作,复杂度全是log元素数量,十分优秀。
(说起来用c[i]-c[i-1]也可以在2*logn的时间单点查询,我甚至还能存一下本来的数组,就是O(1)了啊)
这里的c数组就是树状数组的表示方式了。这个玩意儿真的是靠lowbit()一手撑起来的数据结构了……
lowbit(i)表示i二进制分解后第一个出现1的位置,也是c[i]在原数组中表示的元素和的长度。
lowbit()的代码如下。什么?你问我证明?它就是那样的嘛,我的老师又没讲,怪我喽。
1 int lowbit(int x)//这里的x一定要是非负整数int 2 return x&(-x);
怎么利用呢,就是c[i]=∑o[f],(i-lowbit(i)<f<=i);为什么呢?因为建立的时候就是按这个规则建立的,我这样说你懂了吧?
这个时候应该放一个图了……
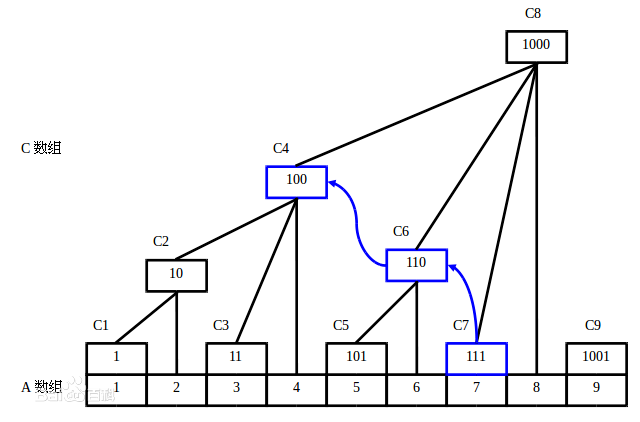
其实只要看这个图自己手推一会就能明白很多了,推荐大家输出一下1-9的lowbit(),一点就通。
假设我们已经建好了,那输出sum[n]就可以把c[n]利用lowbit()向前推,一直推进零里,经过的节点一定完全覆盖了1-n的原数组了
1 for(i=n,ans=0;i!=0;i-=lowbit(i)) 2 ans+=c[i];
证明嘛,自己看图好了。
那么如何建立呢?根据图可以得出c[i]的父节点是c[i+lowbit(i)],那么c[i]加一个值它的父节点们也加一波就完事了。
它的空间复杂度是n,也就是说加到c[n]以后一定停下来,那么就有代码
for(f=i;f<=n;f+=lowbit(f))//n为原数组元素数量 c[f]+=o[i];
修改的话是差不多的。比如把o[x]加t就是这样弄
o[x]+=t; for(;x<=n;x+=lowbif(x)) c[x]+=t;
t当然也能是负数啦。