咕咕咕（凸包）

咕咕咕（凸包）

给出两个点集a和b，\(|a|,|b|\le1e6\)。现在构造点集c，满足\(c_{ij}=a_i+b_j\)，求点集c的凸包。

由于我之前还没有写过关于凸包的博客，现在来总结一发。

平面向量的叉积

我们都知道，平面向量\(a\)和\(b\)的点积是\(|a||b|cos\theta\)，其中\(\theta\)是\(\angle aOb\)，也就是从a开始逆时针旋转到b的角度值。由于点积的分配律（需要几何来证明，这里默认）,\(a*b=(x_1+y_1)*(x_2+y_2)=x_1*x_2+y_1*y_2=x_ax_b+y_ay_b\)（注意\(cos0=1\)，\(cos\pi=-1\)，\(x_a\)这种表示坐标）。

同时，向量a和b的叉积也有定义，为\(|a||b|sin\theta\)，\(\theta\)的含义照旧。由于叉积的分配律（依然跳过证明），\(a\times b=(x_1+y_1)\times(x_2+y_2)=x_1\times y_2+y_1\times x_2=x_ay_b-x_by_a\)。至于为什么，可以自己画图验证所有情况，比较麻烦。

由于向量的夹角\(\theta\in[-\pi,\pi)\)。根据定义，两个平面向量一叉积，就可以通过符号来判断它们旋转的角度。上图：

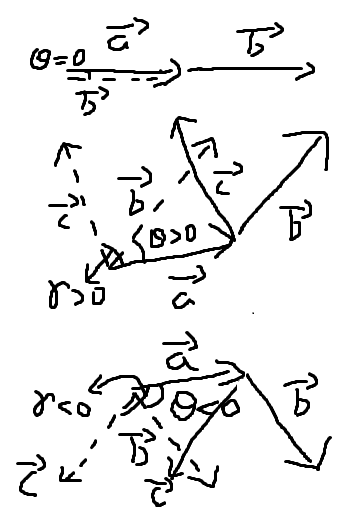
当两向量是逆时针旋转的时候，意味着它们的夹角\(\theta\in(0, \pi)\)，此时\(sin\theta>0\)，叉积大于0。当两向量顺时针旋转，那么\(sin\theta<0\)，叉积小于0。两向量相等时叉积为0。

同时，两向量的叉积还是它们张成的平行四边形的面积。因此，叉积在求凸包的时候非常有用。

Gramgam和Andrew算法

如何求一堆点的凸包？我们先把点按照x轴坐标排序，选出最左边的点作为起点。假设现在已经选了A，B，C三个点：

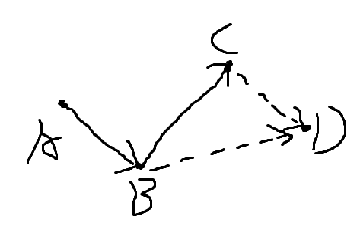
现在要选出点D和它们组成凸包。由于\(\overrightarrow{BC}\)进行顺时针旋转后才和\(\overrightarrow{CD}\)共向，因此\(\overrightarrow{BC}\)不应该是凸包中的边，所以把它撤销。Gramham算法就是先将点极角排序，然后维护一个栈，不停撤销栈顶的边，直到加入的点合法为止。Andrew算法避免了极角排序，而是仅仅按照x轴排序，将算法分成上凸包和下凸包来处理，更方便且不容易错。

此题

讲了这么多，这道题怎么做呢？我们发现，其实就是在一个大凸包的每个顶点上套很多个小凸包，求它们的凸包。有个大力的结论，就是求一遍凸包后，凸包上的点正好绕小凸包走一圈。因此只有两种转移：走到下一个小凸包上的这个点，或者是走到同一个小凸包上的下一个点。复杂度很玄学。

#include <cstdio>
#include <algorithm>
using namespace std;

typedef long long LL;
const LL maxn=1e6+5, maxori=1e3+5;
LL n, m;
LL x[maxn], y[maxn];

struct Point{
    LL x, y;
    Point(LL xx=0, LL yy=0){ x=xx; y=yy; }
}pn[maxn], pm[maxn];
bool operator <(const Point &a, const Point &b){
    return a.x==b.x?a.y<b.y:a.x<b.x; }
bool operator ==(const Point &a, const Point &b){
    return a.x==b.x&&a.y==b.y; }
Point operator +(Point &a, Point &b){
    return Point(a.x+b.x, a.y+b.y); }
struct Vector{
    LL x, y;
    Vector(){ x=0; y=0; }
    Vector(const Point &a, const Point &b){ x=b.x-a.x; y=b.y-a.y; }
};
LL operator *(const Vector &a, const Vector &b){
    return a.x*b.y-b.x*a.y; }

Point bot[maxn], up[maxn];
LL tbot, tup, S;
//gramham要按照极角排序，andrew则只需要按照x轴排序
void Andrew(Point *p, LL &n){
    sort(p, p+n); n=unique(p, p+n)-p;
    tbot=tup=0;
    for (LL i=0; i<n; ++i){
        while (tbot>1&&Vector(bot[tbot-2], bot[tbot-1])*
            Vector(bot[tbot-1], p[i])<=0) --tbot;
        bot[tbot++]=p[i];
    }
    for (LL i=0; i<n; ++i){
        while (tup>1&&Vector(up[tup-2], up[tup-1])*
            Vector(up[tup-1], p[i])>=0) --tup;
        up[tup++]=p[i];
    }
    n=0;
    for (LL i=0; i<tbot-1; ++i) p[n++]=bot[i];
    for (LL i=tup-1; i>0; --i) p[n++]=up[i];
}

Point stack[maxn*2];
LL tail;
int main(){
    scanf("%lld%lld", &n, &m);
    for (LL i=0; i<n; ++i) scanf("%lld%lld", &pn[i].x, &pn[i].y);
    for (LL i=0; i<m; ++i) scanf("%lld%lld", &pm[i].x, &pm[i].y);
    Andrew(pn, n); Andrew(pm, m);
    LL A=0, a=0, S=0; tail=0;
    Point cur; Vector v1, v2;
    do{
        cur=pn[A]+pm[a];
        while (tail>1&&Vector(stack[tail-2], stack[tail-1])
            *Vector(stack[tail-1], cur)<=0) --tail;
        stack[tail++]=cur;
        v1=Vector(cur, pn[(A+1)%n]+pm[a]);  //下一个点只在两者中确定
        v2=Vector(cur, pn[A]+pm[(a+1)%m]);
        if (v1*v2>=0) A=(A+1)%n; else a=(a+1)%m;
    }while(A||a);
    for (LL i=1; i<tail-1; ++i)
        S+=Vector(stack[0], stack[i])*Vector(stack[0], stack[i+1]);
    printf("%lld\n", S);
    return 0;
}