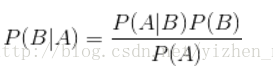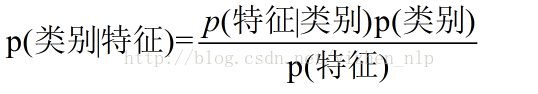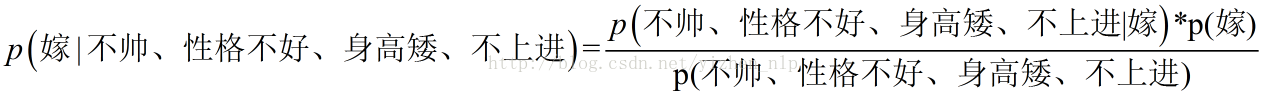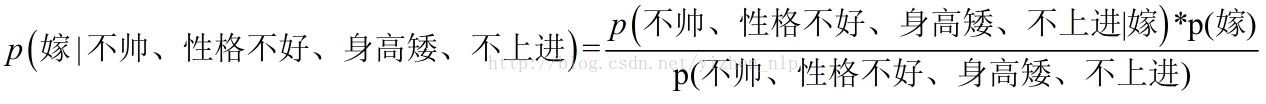朴素贝叶斯分类
贝叶斯分类
贝叶斯分类是一类分类算法的总称,这类算法均以贝叶斯定理为基础,故统称为贝叶斯分类
而朴素朴素贝叶斯分类是贝叶斯分类中最简单,也是常见的一种分类方法
分类问题综述
对于分类问题,其实谁都不会陌生,日常生活中我们每天都进行着分类过程。
例如,当你看到一个人,你的脑子下意识判断他是学生还是社会上的人;
你可能经常会走在路上对身旁的朋友说“这个人一看就很有钱”之类的话,其实这就是一种分类操作
分类的描述
从数学角度来说,分类问题可做如下定义:已知集合和,C= y1,y2...yn 和I=x1,x2...xn
确定映射规则y = f(x),使得任意xi有且仅有一个yi,使得成立 y=f(x)成立
其中C叫做类别集合,其中每一个元素是一个类别,而I叫做项集合(特征集合),其中每一个元
素是一个待分类项,f叫做分类器。分类算法的任务就是构造分类器f。
分类算法的内容是要求给定特征,让我们得出类别,这也是所有分类问题的关键
朴素贝叶斯分类
贝叶斯公式
换个表达形式
我们要解决的问题是: 在特定特征条件下属于某个类别的概率有多少
例题分析
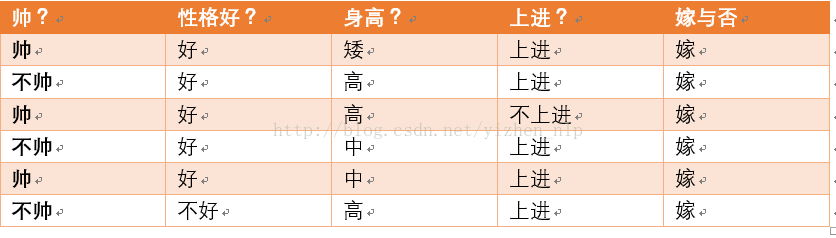
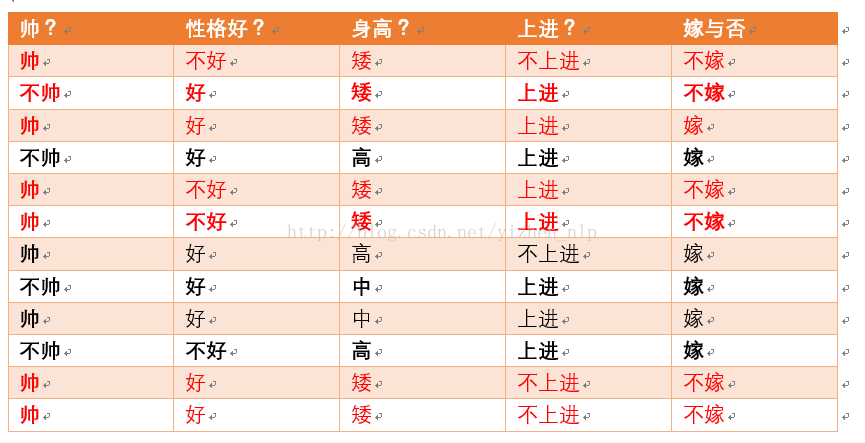
给定的数据如下:

现在给我们的问题是,如果一对男女朋友,男生想女生求婚,男生的四个特点分别是不帅,性格不好,身高矮,不上进,请你判断一下女生是嫁还是不嫁?
转为数学问题就是比较p(嫁|(不帅、性格不好、身高矮、不上进))与p(不嫁|(不帅、性格不好、身高矮、不上进))的概率,谁的概率大,我就能给出嫁或者不嫁的答案!
套用朴素贝叶斯公式
朴素贝叶斯算法的朴素一词解释
那么我只要求得
p(不帅、性格不好、身高矮、不上进|嫁)
p(不帅、性格不好、身高矮、不上进)
p(嫁)
下面我分别求出这几个概率,就得到最终结果。
假设 p(不帅、性格不好、身高矮、不上进|嫁)
= p(不帅|嫁)*p(性格不好|嫁)*p(身高矮|嫁)*p(不上进|嫁)
这也就是为什么朴素贝叶斯分类有朴素一词的来源,朴素贝叶斯算法是假设各个特征之间相互独
立,那么这个等式就成立了!
这一假设使得朴素贝叶斯法变得简单,但有时会牺牲一定的分类准确率。
我们将上面公式整理一下如下:
我们的任务是要求出特定特征下是嫁|不嫁 那个概率更大,对比两个公式分母相同,那只需要计算两个情况的分子
p(嫁)=?
首先我们整理训练数据中,嫁的样本数如下:
则 p(嫁) = 6/12(总样本数) = 1/2
p(性格不好|嫁)= ?统计满足样本数如下:
p(性格不好|嫁)=1/6
p(矮|嫁) = ?统计满足样本数如下:
则p(矮|嫁) = 1/6
p(不上进|嫁) = ?统计满足样本数如下:
则p(不上进|嫁) = 1/6
= (1/2)(1/6)(1/6)(1/6)(1/2)/分母相同
同样原理 计算下p(不嫁|不帅,性格不好,身高矮,不上进)
p (嫁|不帅、性格不好、身高矮、不上进)
=(1/2)*(1/6)*(1/6)*(1/6)*(1/2)/分母
=(1/144)/分母
p (不嫁|不帅、性格不好、身高矮、不上进)
= ((1/6*1/2*1*1/2)*1/2)/分母
= (1/24)/分母
于是有p (不嫁|不帅、性格不好、身高矮、不上进)>p (嫁|不帅、性格不好、身高矮、不上进)
所以我们根据朴素贝叶斯算法可以给这个女生答案,是不嫁!!!!
以上公式是如何得来的呢
韦恩图
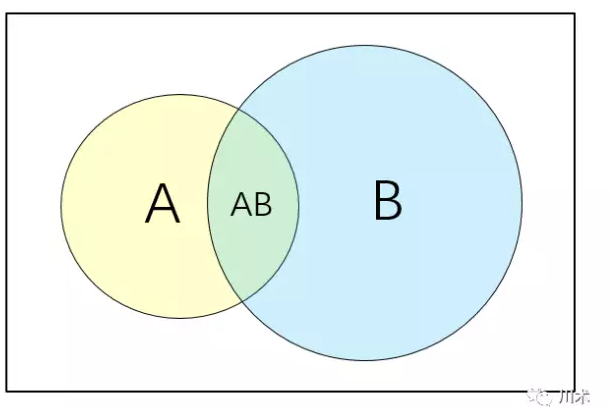
如上面的韦恩图,我们用矩形表示一个样本空间,代表随机事件发生的一切可能结果。
的在统计学中,我们用符号P表示概率,A事件发生的概率表示为P(A)
A事件与B事件同时发生的概率表示为P(A∩B),或简写为P(AB)即两个圆圈重叠的部分。
A或者B至少有一个发生的概率表示为P(A∪B),即圆圈A与圆圈B覆盖的区域。
在B事件发生的基础上发生A的概率表示为P(A|B),这便是条件概率,图形上 它表示AB重合的面积比上B的面积
统计学基本概念
- P(A) A事件发生的概率
- p(AB)或p(A∩B) 事件AB同时发生的概率
- p(A|B) 事件B发生了情况下发生事件A的概率
条件概率公式
由维恩图可知: p(AB) = p(B)p(A|B) = p(A)p(B|A)
P(A|B)=P(AB)/P(B)=p(A)p(B|A)/p(B)
条件概率是理解全概率公式和贝叶斯公式的基础,可以这样来考虑,
如果P(A|B)大于P(A)则表示B的发生使A发生的可能性增大了。
在条件概率中,最本质的变化是样本空间缩小了——由原来的整个样本空间缩小到了给定条件的样本空间
全概率公式
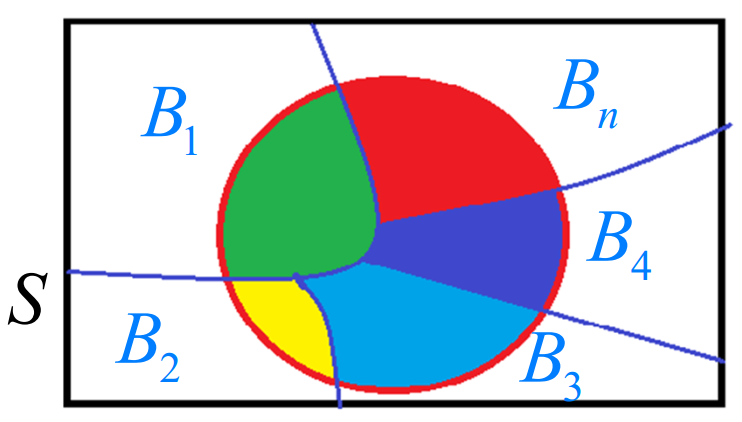
1.事件组B1,B2,.... 满足 B1,B2....两两互斥,即 Bi ∩ Bj = ∅ ,i≠j , i,j=1,2,....,
且P(Bi) >0,i=1,2,....;
2.B1∪B2∪....=Ω ,则称事件组 B1,B2,...是样本空间Ω的一个划分
设 B1,B2,...是样本空间Ω的一个划分,A为任一事件,则:
P(A)=P(AB1)+P(AB2)+....+P(ABn)
=P(A|B1)P(B1)+P(A|B2)P(B2)+...+P(A|Bn)P(PBn)
上式即为全概率公式(formula of total probability)
全概率公式的意义在于,当直接计算P(A)较为困难,而P(Bi),P(A|Bi) (i=1,2,...)的计算较为简单
时, 可以利用全概率公式计算P(A)。
思想就是,将事件A分解成几个小事件,通过求小事件的概率,然后相加从而求得事件A的概率,而将事
件A进行分割的时候,不是直接对A进行分割,而是先找到样本空间Ω的一个个划分B1,B2,...Bn,这样事件
A就被事件AB1,AB2,...ABn
分解成了n部分,即A=AB1+AB2+...+ABn, 每一Bi发生都可能导致A发生相应的概率是P(A|Bi),由加法公式得
P(A)=P(AB1)+P(AB2)+....+P(ABn)
=P(A|B1)P(B1)+P(A|B2)P(B2)+...+P(A|Bn)P(Bn)
事件A在事件B(发生)的条件下的概率,与事件B在事件A的条件下的概率是不一样的;然而,这两者
是有确定的关系,贝叶斯定理就是这种关系的陈述


这个公式本身平平无奇,无非就是条件概率的定义加上全概率公式一起作出的一个推导而已。但它所表达的意义却非常深刻。
全概率公式就是一个“原因推结果”的过程
但贝叶斯公式却恰恰相反,研究造成结果发生的原因 是XX原因造成的可能性有多大,即“结果推原因”。
实例1
发报台分别以概率0.6和0.4发出信号“∪”和“—”。由于通信系统受到干扰,当发出信号“∪”时,
收报台分别以概率0.8和0.2受到信号“∪”和“—”;又当发出信号“—”时,收报台分别以概率0.9和0.1收到信号“—”和“∪”。
求当收报台收到信号“∪”时,发报台确系发出“∪”的概率。
p(发出U|收到U) = p(发出u) * P(收到U|发出U) / p(真实发出U)*p(收到u|真实发出u) + p(假发出U)* p(收到u|假发出u
==> 0.6*0.8 / (0.6*0.8 + 0.1*0.4) =0.923
实例2
一所学校里面有 60% 的男生,40% 的女生。男生总是穿长裤,女生则一半穿长裤一半穿裙子。
假设你走在校园中,迎面走来一个穿长裤的学生(很不幸的是你高度近似,你只看得见他(她)穿的是否长裤,
而无法确定他(她)的性别),你能够推断出他(她)是男生的概率是多大吗?
p(男生|长裤) = p(男生) * p(长裤|男生) / p(长裤)
= 0.6 * 1 / 0.6*1 + 0.4*0.5 = 0.6/0.8 = 6/8
工程应用推导过程:

-
p(y=ck) = y类别的概率 = y类别出现的次数/总类别数
-
p(xi|y) = xi在y分类中出现的总次数/样本中该分类的次数
不同模型下的p(xi|y):
-
高斯模型 当特征是连续变量的时候,运用多项式模型就会导致很多P(xi|yk)=0(不做平滑的情况下),此时即使做平滑,所得到的条件概率也难以描述真实情况。所以处理连续的特征变量,应该采用高斯模型
-
多项式 当特征是离散的时候,使用多项式模型。多项式模型在计算先验概率P(yk)和条件概率P(xi|yk)时,会做一些平滑处理,具体公式为: P(yk)=Nyk+α / N+kα
N是总的样本个数,k是总的类别个数,Nyk是类别为yk的样本个数,α是平滑值
P(xi|yk)=Nyk,xi+α / Nyk+nα
Nyk是类别为yk的样本个数,n是特征的维数,Nyk,xi是类别为yk的样本中,第i维特征的值是xi的样本个数,α是平滑值
当α=1时,称作Laplace平滑,当0<α<1时,称作Lidstone平滑,α=0时不做平滑。
如果不做平滑,当某一维特征的值xi没在训练样本中出现过时,会导致P(xi|yk)=0,从而导致后验概率为0。加上平滑就可以克服这个问题。
-
伯努利
与多项式模型一样,伯努利模型适用于离散特征的情况,所不同的是,伯努利模型中每个特征的取值只能是1和0(以文本分类为例,某个单词在文档中出现过,则其特征值为1,否则为0).
伯努利模型中,条件概率P(xi|yk) 的计算方式是:
当特征值xi为1时,P(xi|yk)=P(xi=1|yk)
当特征值xi 为0时,P(xi|yk)=1−P(xi=1|yk)
数据溢出:
为防止连续乘法时每个乘数过小,而导致的浮点数溢出(太多很小的数相乘结果为0,或者不能正确分类)
当计算乘积 p(w0|ci) * p(w1|ci) * p(w2|ci)... p(wn|ci) 时,由于大部分因子都非常小,
所以程序会下溢出或者得到不正确的答案。(用 Python 尝试相乘许多很小的数,最后四舍五入后会得到 0)
一种解决办法是对乘积取自然对数。在代数中有 ln(a * b) = ln(a) + ln(b),
于是通过求对数可以避免下溢出或者浮点数舍入导致的错误。采用自然对数进行处理不会有任何损失
流程
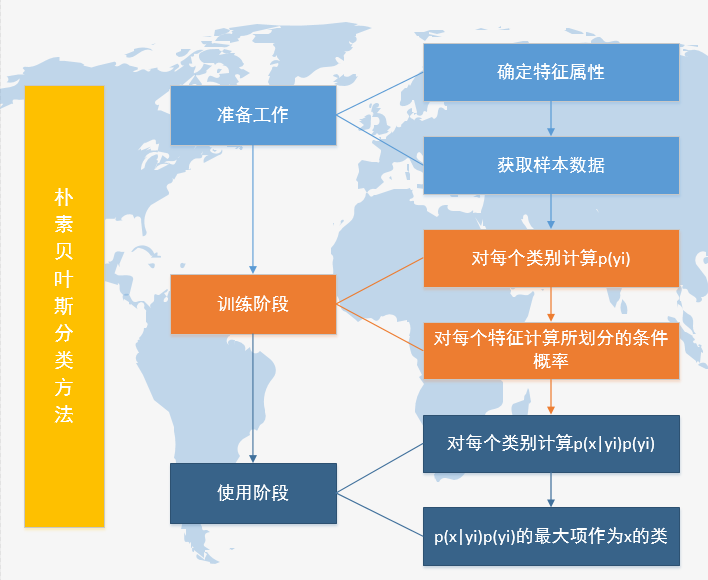
数据的训练
-
留出法
留出法的步骤相对简单,直接将数据集D划分为两个互斥的集合,其中一个集合作为训练集S,另一个作为测试T。在S上训练出模型后,用T来评估测试误差,作为泛化误差的估计。训练/测试集的划分要尽可能保持数据分布的一致性,避免因数据划分过程引入额外偏差而对最终结果产生影响。
留出法的一个缺点是,训练集S与测试集T的划分比例不好确定。若令训练集S包含绝大多数样本,则训练出的模型可能更接近与用D训练出的模型,但由于T比较小,评估结果可能不够稳定准确;若令测试集T多包含一些样本,则训练集S与D差别更大了,被评估的模型与用D训练出的模型相比可能有较大差别,从而降低了评估结果的保真性
-
交叉验证法
“交叉验证法”先将数据集D划分为k个大小相似的互斥子集。然后,每次用k-1个子集的并集作为训练集,余下的那个子集作为测试集,如下图所示,

-
自助法
我们希望评估的是用D训练出的模型。但在留出法和交叉验证法中,由于保留了一部分样本用于测试,因此实际评估的模型所使用的训练集比D小,
这必然会引入一些因训练样本规模不同而导致估计偏差。交叉验证法受训练样本规模影响较小,但计算复杂度又太高了。有没有什么办法可以减少
训练样本规模不同造成的影响,同时还能比较高效进行试验评估呢?
“自助法”是一个比较好的解决方案。给定包含m个样本的数据集D,我们对它进行采样产生数据集D':每次随机从D中挑选一个样本,并将其拷贝放
入D'中,然后再将该样本放回数据集D中,使得该样本在下次采样时仍有可能被采到;这个过程重复执行m次后,我们得到了包含m个样本的数据集
D',这就是我们自助采样的结果。我们将D'作为训练集,将D-D‘(集合减法)作为测试集。
自助法在数据集较小、难以有效划分训练/测试集时很有用;此外,自助法能从初始数据集中产生多个不同的训练集,这对集成学习等方法有很大
的好处。然而,自助法产生的数据改变了初始数据集的分布,这会引入估计偏差。因此,在初始数据量足够是,留出法和交叉验证法更常用一些。
评估
正确率(查准率)
正确率是针对我们预测结果而言的,它表示的是预测为正的样本中有多少是对的。那么预测为正
就有两种可能了,一种就是把正类预测为正类,另一种就是把负类预测为正类
正确率 = 提取出的正确信息条数 / 提取出的信息条数
召回率(查全率)
召回率是针对我们原来的样本而言的,它表示的是样本中的正例有多少被预测正确了。那也有两
种可能,一种是把原来的正类预测成正类,另一种就是把原来的正类预测为负类
召回率 = 提取出的正确信息条数 / 样本中的正确信息条数
F1
综合这二者指标的评估指标,用于综合反映整体的指标
F1 = 正确率 * 召回率 * 2 / (正确率 + 召回率)
例子
不妨举这样一个例子:
某池塘有1400条鲤鱼,300只虾,300只鳖,现在以捕鲤鱼为目的
撒一大网,逮着了700条鲤鱼,200只虾,100只鳖。那么,这些指标分别如下:
正确率 = 700 / (700 + 200 + 100) = 70%
召回率 = 700 / 1400 = 50%
F值 = 70% * 50% * 2 / (70% + 50%) = 58.3%
如果把池子里的所有的鲤鱼、虾和鳖都一网打尽,这些指标又有何变化:
正确率 = 1400 / (1400 + 300 + 300) = 70%
召回率 = 1400 / 1400 = 100%
F值 = 70% * 100% * 2 / (70% + 100%) = 82.35%
由此可见,正确率是评估捕获的成果中目标成果所占得比例;召回率,顾名思义,就是从关注领域中,召回目标类别的比例;
而F值,则是综合这二者指标的评估指标,用于综合反映整体的指标。


准确率就是P = TP/(TP+FP) 大白话就是“你的预测有多少是对的”
召回率就是R = TP/(TP+FN) 大白话就是“正例里你的预测覆盖了多少”
真正例 TP = 700 [我要鱼]
假正例 FP = 300 [我要的是鱼, 你给我别的 都认为是假正例]
假反例 FN = 700 [本来是鱼,却没有当做鱼给我 1400-700]
真反例 FP = 300 [本来不是鱼,却当成鱼给我 300+300-200-100]
正确率 = TP/TP+FP = 700/(700+300)
召回率 = TP/TP+FN = 700/(700+700)
项目实战 文章自动分类
-
第一阶段获取样本数据
爬虫系统在抓取特定的分类的文章已经定义好分类
目前分类有: 股票/外汇/期货/黄金/基金/科技/数字货币/收藏/保险/P2P/理财/信托/债券/银行/房地产 共有15个分类
采集的样本共有 5521条数据 其中训练集 4416 测试数据 1105
-
数据的训练
测试数据收集方式: 留出法 80% 训练 20% 测试
准确率: 取前2个 83%左右, 取第一个72%左右
召回率: -- 暂未开发
F1: --暂未开发
样本集: 增量方式 每月拉取一次,增量同步信息,效果评估没问题投入生产上
训练输出: 每个单词在分类下的概率 P(xi|yj) & 分类概率 P(y)
-
分类的使用
入参: [文章内容]
1.提取关键词
2.累加P(xi|yj)概率 + P(yj)
出参: [文章属于所有分类的列表及概率值]
-
持续优化及问题
-
提高样本分类的正确性/数据均匀分布/足够的数量 (很重要前提)
-
增加了关键词的权重
-
stop_word 完善,去掉不相关的词或者词频比较高中性词的
-
训练过程中不同长度文章提取不同数量的关键词 <1000 10 tags, 1000~3000 15 tags, >3000 20 tags
-
文章内容很少的忽略,不进入训练样本 目前<300字符 忽略
-
关键词小写,防止大小写问题不匹配
-
-
问题
-
在前面提到的防止浮点数连乘 数据溢出 整体取对数 log2(x) x(0,1) 结果是负数, 累加是越来越小
目前采取的方式是 曲线平移 log2(1+x) 保证数据的正数
-


2. 分类过程没有出现的词汇不进行计算 有分不出类别的可能
3. 纯手写没有使用开源框架
4. 目前样本数据噪声比较大
总结
-
朴素贝叶斯
朴素贝叶斯算法是建立在每一个特征值之间时独立的基础上的监督学习分类算法,而这也是称 他为 “朴素”贝叶斯的缘由 贝叶斯公式 + 特征条件独立假设 = 朴素贝叶斯 -
流程 1.准备数据/采集样本
2.训练数据 计算p(yi)/p(wi|yi) 高斯/伯努利/多项式 3.数据的测试验证 留出法/交叉验证/自助 准确率/召回率/F1 4.使用 简单累加 -
优化
1.保证样本数据准确和数据分布均匀 2.防止数据溢出 取对数 3.防止概率为0情况 拉普拉斯平滑 4.stop_word 整理 5.英文大小写统一处理 6.不同长度文章提取不同个数个关键词