【BZOJ1227】【SDOI2009】虔诚的墓主人

题目描述

小W是一片新造公墓的管理人。公墓可以看成一块 $N×M$ 的矩形，矩形的每个格点，要么种着一棵常青树，要么是一块还没有归属的墓地。

当地的居民都是非常虔诚的基督徒，他们愿意提前为自己找一块合适墓地。为了体现自己对主的真诚，他们希望自己的墓地拥有着较高的虔诚度。

一块墓地的虔诚度是指以这块墓地为中心的十字架的数目。一个十字架可以看成中间是墓地，墓地的正上、正下、正左、正右都有恰好 $k$ 棵常青树。

小W希望知道他所管理的这片公墓中所有墓地的虔诚度总和是多少。

输入输出格式

输入格式：

输入文件 religious.in 的第一行包含两个用空格分隔的正整数 $N$ 和 $M$ ，表示公墓的宽和长，因此这个矩形公墓共有 $(N+1) ×(M+1)$ 个格点，左下角的坐标为 $(0, 0)$ ，右上角的坐标为 $(N, M)$ 。

第二行包含一个正整数 $W$ ，表示公墓中常青树的个数。

第三行起共 $W$ 行，每行包含两个用空格分隔的非负整数 $x_i$ 和 $y_i$ ，表示一棵常青树的坐标。输入保证没有两棵常青树拥有相同的坐标。

最后一行包含一个正整数 $k$ ，意义如题目所示。

输出格式：

输出文件 religious.out 仅包含一个非负整数，表示这片公墓中所有墓地的虔诚度总和。为了方便起见，答案对 $2,147,483,648$ 取模。

输入输出样例

输入样例：

5 6
13
0 2
0 3
1 2
1 3
2 0
2 1
2 4
2 5
2 6
3 2
3 3
4 3
5 2
2

输出样例：

6

说明

图中，以墓地 $(2, 2)$ 和 $(2, 3)$ 为中心的十字架各有 $3$ 个，即它们的虔诚度均为 $3$ 。其他墓地的虔诚度为 $0$ 。

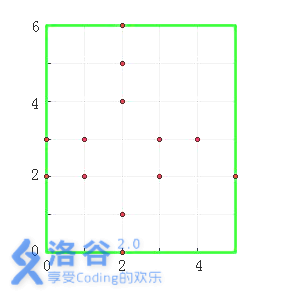
对于 $30\%$ 的数据，满足 $1 \leq N, M \leq 10^3$ 。

对于 $60\%$ 的数据，满足 $1 \leq N, M \leq 10^6$ 。

对于 $100\%$ 的数据，满足 $1 \leq N, M \leq 10^9，$$0 \leq x_i \leq N，0 \leq y_i \leq M，$$1 \leq W \leq 100,000，$$1 \leq k \leq 10$ 。

存在 $50\%$ 的数据，满足 $1 \leq k \leq 2$ 。

存在 $25\%$ 的数据，满足 $1 \leq W \leq 10^4$ 。

题解

我们记墓地 $(i, j)$ 的正上，正下，正左，正右的树的数量分别为 $up(i, j),$$down(i, j),$$left(i, j),$$right(i,j)$ 。

首先考虑暴力的做法
可以发现，每一个墓地的答案 $ans(i,j) = C_{up(i,j)}^{k}C_{down(i,j)}^{k}C_{left(i,j)}^{k}C_{right(i,j)}^{k}$ 。很明显是 $O(W^2)$ 。
由于点多树少，所以我们可以分区间考虑。
由于同一行相邻的两棵树之间的墓地的 $left(i, j),$$right(i,j)$ 都是相等的，我们可以直接统计，即为

$$C_{left(i,j)}^{k}C_{right(i,j)}^{k}\sum_{t = j_1 + 1}^{j_2 - 1}C_{up(i,t)}^{k}C_{down(i,t)}^{k}$$

于是就可以按 $y$ 排序树后用树状数组维护了。由于两个端点对答案无影响，可以先统计答案，再处理修改。具体详见代码。

复杂度 $O(Wlog_2W)$ 。

My Code

（自然溢出最好别用，可能会有bug）

/**************************************************************
    Problem: 1227
    User: infinityedge
    Language: C++
    Result: Accepted
    Time:3552 ms
    Memory:14188 kb
****************************************************************/

#include <iostream>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <cstdio>

using namespace std;
typedef long long ll;
const ll mod = 2147483648ll;

struct node{
    int x, y;
}d[100005];

ll C[100005][11];

int tx[100005], ty[100005];
int n, r, c, k;

void pre(){
    C[0][0] = 1;
    for(int i = 1; i <= n; i ++){
        C[i][0] = 1;
        for(int j = 1; j <= k; j ++){
            C[i][j] = (C[i - 1][j - 1] + C[i - 1][j]) % mod;
        }
    }
}


ll ds[200005];
ll ans = 0;
inline int lowbit(int x){
    return x & -x;
}

void add(ll *bit, int pos, ll v){
    for(int i = pos; i <= 2 * n; i += lowbit(i)){
        bit[i] += v;
        bit[i] = (bit[i] + mod) % mod;
    }
}

ll query(ll *bit, int pos){
    ll sum = 0;
    for(int i = pos; i; i -= lowbit(i)){
        sum += bit[i];
        sum = sum % mod;
    }
    return sum;
}

int cmp(node a, node b){
    return a.y == b.y ? a.x < b.x : a.y < b.y;
}

int rr[100005], dr[100005], ur[100005];
void solve(){
    for(int i = 1; i <= n; i ++){
        dr[d[i].x] ++;
    }
    for(int i = 1; i <= n; i ++){
        rr[d[i].y] ++;
    }
    int cl = 0, cr = 0;
    for(int i = 1; i <= n; i ++){
        if(d[i].y != d[i - 1].y){
            cl = 0, cr = rr[d[i].y];
        }else{
            cl++; cr--;
            if(tx[d[i].x] - tx[d[i - 1].x] != 1){
                ans = (ans + C[cl][k] % mod * C[cr][k] % mod * (query(ds, d[i].x - 1) - query(ds, d[i - 1].x) + mod) % mod) % mod;
            }
        }

        add(ds, d[i].x, -(C[ur[d[i].x]][k] * C[dr[d[i].x]][k] % mod));
        dr[d[i].x] --;
        ur[d[i].x] ++;
        add(ds, d[i].x, (C[ur[d[i].x]][k] * C[dr[d[i].x]][k] % mod));
    }
}

int main(){
    scanf("%d%d", &r, &c);
    scanf("%d", &n);
    for(int i = 1; i <= n; i ++){
        scanf("%d%d", &d[i].x, &d[i].y);
    }

    for(int i = 1; i <= n; i ++){
        tx[i] = d[i].x;
    }
    sort(tx + 1, tx + n + 1);
    for(int i = 1; i <= n; i ++){
        d[i].x = lower_bound(tx + 1, tx + n + 1, d[i].x) - tx;
    }

    for(int i = 1; i <= n; i ++){
        ty[i] = d[i].y;
    }
    sort(ty + 1, ty + n + 1);
    for(int i = 1; i <= n; i ++){
        d[i].y = lower_bound(ty + 1, ty + n + 1, d[i].y) - ty;
    }
    sort(d + 1, d + n + 1, cmp);
    scanf("%d", &k);
    pre();
    solve();
    printf("%lld\n", ans);
    return 0;
}