手把手教你写线段树

线段树入门教程

线段树往往会是各位OIer接触的第一种玄学数据结构，awa这东西很不好理解，但确实很有用。我还是争取写一篇对刚入门的新手友好的文章对线段树加一说明，手把手教大家写线段树。

线段树是什么？

二叉树大家知道吗？就是每一个节点会有左右两个子节点，子节点又有子节点……总起来就是二叉树。二叉树在玄学数据结构中会经常用到，比如splay，treap，乃至红黑树等等魔法玩意。这些不用管，就了解一下二叉树就好了。

很好理解对吗？
线段树就是基于二叉树的一种数据结构，用于解决在一段区间上修改和查询的问题。
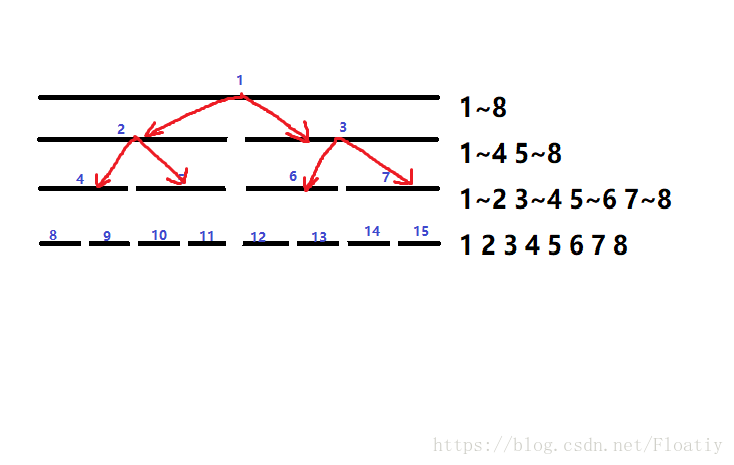
画一张易于理解的图

好吧我承认图画的吃藕。。蓝色是小标号，忽略就好了。
线段树的本质，就是将一段区间（图中的1~8）经过多次二分，拆成一个一个的单点（图中的1 2 3 4 5 6 7 8）
嗯没错这个就是线段树

为什么选择线段树？

因为快。。。
举个例子，比如我们要将2~5号点加上1，朴素做法是一个一个相加，时间复杂度为O(n)，而我们如果使用线段树，会是这样操作的：

---

我们从线段树的顶端开始；
如果当前枚举到的区间被要加v的区间完全包含，就在这个区间进行加法操作，把这个区间加上要加的数v乘上这段区间的元素（点）个数，再记录一下这段区间被加过v，就不再往下枚举了。
如果不被完全包含，就接着二分，枚举当前这一段的前半段和后半段

---

这个就是线段树的原理辣，努力理解一下。

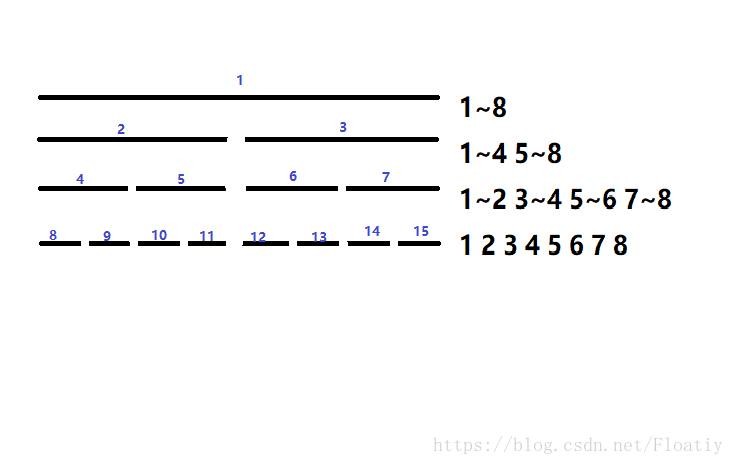
还是拿1~8那个图举例子。
我们从最上面开始，发现当前枚举到的区间是1~8，而要修改的区间是2~5，并没有完全包含，于是我们开始枚举它的前半段和后半段（1~4和5~8）。

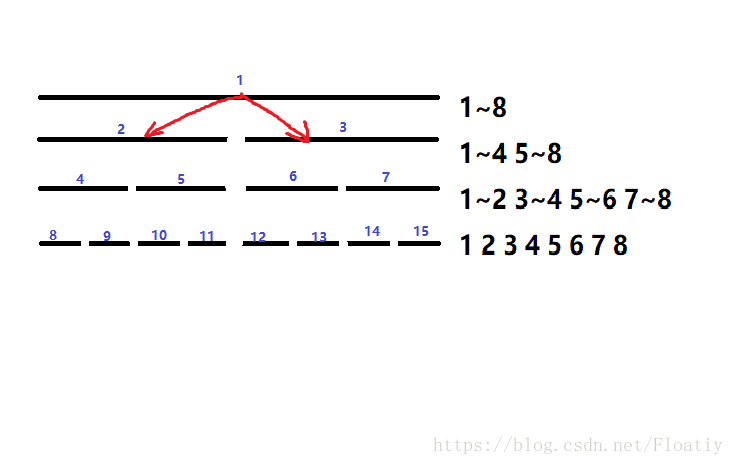
再枚举1~4和5~8，发现仍没有被2~5完全包含，所以继续二分，枚举1~2，3~4，5~6，7~8.

注意！这时我们发现3~4被2~5完全包含了！！

将3~4这段区间加上元素个数（右端点-左端点+1）× 要加的数v，不再二分它。
然后发现其它区间仍然不满足，接着二分其它的区间（1~2，5~6，7~8）

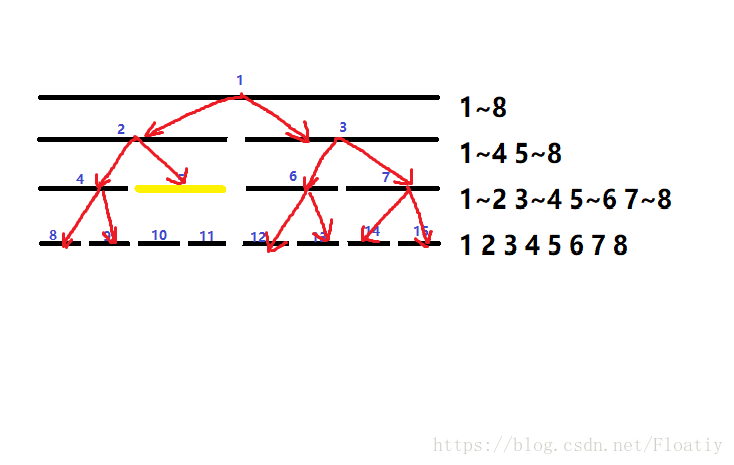
现在我们的区间经过层层二分已经变成单点了，我们把目前被包含的单点加上v；

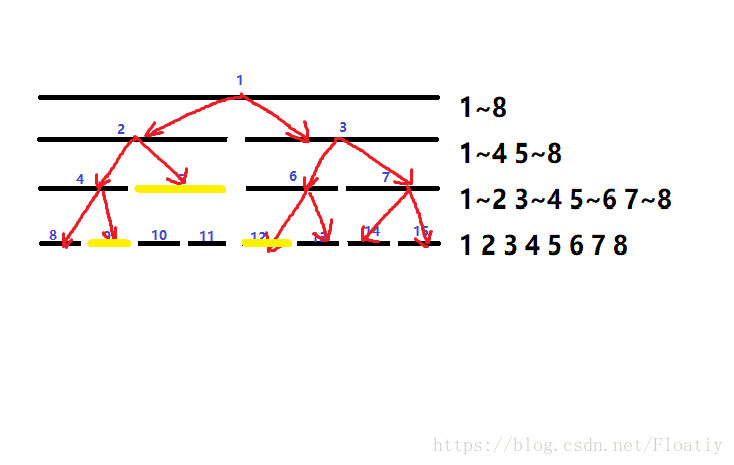
那我们的区间修改就完成了，总共只修改了图中亮黄色的3段区间。
我们得出结论：

线段树区间修改的时间复杂度为O(logn)！

这就是我们选择线段树的原因，至此我们已经完成了线段树区间修改的手动模拟。

下面我们来模拟一下建树的过程

我们也是从上到下不断二分，如果到达了最底层（也就是单点）就输入当前点的值。这个很好理解，就不模拟了。

然后是询问

其实询问和区间加法是一样的，都是从上而下进行二分，从线段树的顶端开始；
如果当前枚举到的区间被要加v的区间完全包含，就在把ans加上当前区间的值，不再往下枚举了。
如果不被完全包含，就接着二分，枚举当前这一段的前半段和后半段。

线段树怎么写？

啊我手把手教大家好了，这个确实是很难的东西。
emmm先写个结构体

#include<iostream>
#include<cstdio>
using namespace std;
int n,m,ans;
struct Tree{
    int sum;
    int tag;//注意！
}

这个tag，是线段树的精髓，也就是人们常说的“lazy标记”。
具体是什么呢？
记得我之前模拟的时候，“再记录一下这段区间被加过v，就不再往下枚举了”，这个tag就是用来记录这段区间被加过v（不是这段总共加v，是这段的每个单点加v），这样就避免了对这段区间之下的子区间进行枚举，从而使时间复杂度从nlogn降至了logn，而使得线段树优于朴素的修改。

---

tips：在代码中，pos表示当前处理的区段编号，L和R表示当前处理区段的左右端点，ll和rr表示要进行处理或询问的

接下来我们写build（建树）

void build(int L,int R,int pos)
{
    if(L == R)
    {
        scanf("%d",&t[pos].sum);
        return;
    }
    int mid = (L + R)>>1;
    build(L,mid,pos<<1);
    build(mid + 1,R,pos<<1|1);
    update(pos);
}
void update(int pos)
{
    t[pos].sum = t[pos<<1].sum + t[pos<<1|1];
    return;
}

说一下，pos是当前节点标号，也就是我图中的小蓝数字。
pos<<1和pos<<1|1是位运算，就是pos*2和pos*2+1，也就是pos的两个子区间，大家有兴趣的话可以对着我的图验证一下。
L R代表当前区间的左右节点，L==R时，说明此区间为单点，输入数据，然后结束就可以了。如果没到单点，就接着二分。
那这个update是干嘛的呢？
答：维护当前区间的父亲区间的值是正确的（正确意为：不需要加上tag的值就已经是事实上的sum）。

---

接下来我们写区间修改，这里以加法为例。

void add(int L,int R,int ll,int rr,int pos,int v)
{
    if(ll <= L && R <= rr)
    {
        t[pos].sum += v * (R - L + 1);
        t[pos].tag += v;
        return;
    }
    if(L == R) return;
    pushdown(L,R,pos);
    int mid = (L + R) >> 1;
    add(L,mid,ll,rr,pos<<1,v);
    add(mid + 1,R,ll,rr,pos<<1|1,v);
    update(pos);
}
void pushdown()
{
    if(!t[pos].tag) return;
    int mid = (L + R) >> 1;
    t[pos<<1].sum += t[pos].tag * (mid - L);
    t[pos<<1|1].sum += t[pos].tag * (R - (mid + 1) + 1);
    t[pos<<1].tag += t[pos].tag;
    t[pos<<1|1].tag += t[pos].tag;
    t[pos].tag = 0;
}

所以又有了一个糟糕的东西叫 pushdown 。
什么东西呢？
它的用途跟update很像，其实就是update的反演。
记得我们之前处理的时候是怎么做的吗？
“再记录一下这段区间被加过v，就不再往下枚举了”
那万一我们需要处理它下面的区段怎么办呢？下面的区段不一定经过修改啊。
嗯这就需要我们的pushdown操作了，在每次修改时将lazy标记下放到下面的子区间，同时对子区间的值进行修改，保证在修改时这段区间的值是正确的。
加法已经模拟过了，不再赘述了。

---

区间查询的思路和区间修改差不多：

void query(int L,int R,int ll,int rr,int pos)
{
    if(ll <= L && R <= rr)
    {
        ans += t[pos].sum;
        return;
    }
    if(L == R) return;
    pushdown(L,R,pos);
    int mid = (L + R) >> 1;
    query(L,mid,ll,rr,pos<<1);
    query(mid + 1,R,ll,rr,pos<<1|1)
    return;
}

也是从上往下进行二分，思路和区间修改一样。

---

最后上完整代码：

#include<iostream>
#include<cstdio>
using namespace std;

const int MAXN = 1e5 + 5;

int n,m,ans;
struct Tree{
    int sum;
    int tag;
}t[MAXN<<2];//空间需要开到nlogn

void update(int pos)
{
    t[pos].sum = t[pos<<1].sum + t[pos<<1|1].sum;
}

void build(int L,int R,int pos)
{
    if(L == R)
    {
        scanf("%d",&t[pos].sum);
        return;
    }
    int mid = (L + R) >> 1;
    build(L,mid,pos<<1);
    build(mid + 1,R,pos<<1|1);
    update(pos);
}

void pushdown(int L,int R,int pos)
{
    if(!t[pos].tag) return;
    int mid = (L + R) >> 1;
    t[pos<<1].sum += t[pos].tag * (mid - L);
    t[pos<<1|1].sum += t[pos].tag * (R - (mid + 1) + 1);
    t[pos<<1].tag += t[pos].tag;
    t[pos<<1|1].tag += t[pos].tag;
    t[pos].tag = 0;
}



void add(int L,int R,int ll,int rr,int pos,int v)
{
    if(ll <= L && R <= rr)
    {
        t[pos].sum += v * (R - L + 1);
        t[pos].tag += v;
        return;
    }
    if(L == R) return;
    pushdown(L,R,pos);
    int mid = (L + R) >> 1;
    add(L,mid,ll,rr,pos<<1,v);
    add(mid + 1,R,ll,rr,pos<<1|1,v);
    update(pos);
}

void query(int L,int R,int ll,int rr,int pos)
{
    if(ll <= L && R <= rr)
    {
        ans += t[pos].sum;
        return;
    }
    if(L == R) return;
    pushdown(L,R,pos);
    int mid = (L + R) >> 1;
    query(L,mid,ll,rr,pos<<1);
    query(mid + 1,R,ll,rr,pos<<1|1)
    return;
}

int main()
{
    ___________________________
    return 0;
}

有讲的不好的地方欢迎留言指出！