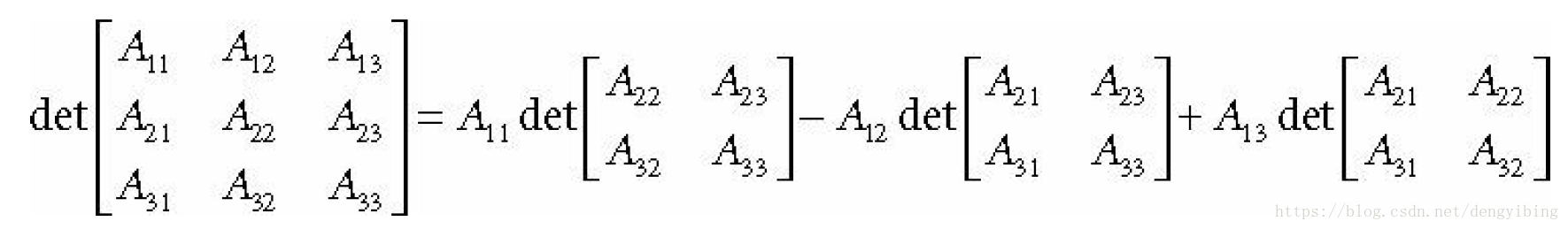DirectX数学介绍

本文为 Introduction to 3D Game Programming with DirectX 11 读书笔记

坐标系统

DirectX使用的是左手坐标系，使用左手坐标系计算叉乘的时候方向用左手决定
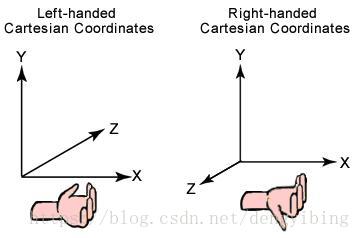
左右手坐标系
书上给的图如下

w = u \times v = (u_{y} v_{z} - u_{z} v_{y}, u_{z} v_{x} - u_{x} v_{z}, u_{x} v_{y} - u_{y} v_{x})

$w = u \times v = (u_yv_z-u_zv_y,u_zv_x-u_xv_z,u_xv_y-u_yv_x)$
左手坐标系计算叉乘

Vector Algebra

win10已经把DirectX11集成到了windows SDK中，所以如果是使用win10做开发，则不需要手动下载DirectX11的类库。

对于D3D11，数学计算库用XNA Math library，该库提供了SIMD指令的封装，SIMD是单指令多数据，简而言之就是计算速度更快，所以在每当要做计算的时候就要对矩阵、向量等做类型转换。
要使用XNA Math library只要，原先是xnmath.h，但是早就不可用了，下面是正确的

#include <DirectXMath.h>
#include <DirectXPackedVector.h>

using namespace DirectX; 
using namespace DirectX::PackedVector;

SIMD一条指令使用多个数据，比如4个32位的数都放到一个128位的寄存器上，然后执行一次运算指令，得到输出，这样对于同样的操作，执行4次指令，得到输出要快大约4倍。

XNA Math定义的可以执行SIMD的Vector类型是 XMVECTOR，这是一个128位的类型，可以用SIMD指令处理4个32位的浮点数。如果机器支持SSE2，则将会有定义

typedef __m128 XMVECTOR;

XMVECTOR需要16位对齐，对于局部变量和全局变量都是如此，上面解释了SIMD，需要把整块数据都移到寄存器上，但这都是自动完成的。

对于一般的类中使用的变脸则使用一般的struct类型就行了，只有在需要计算的时候才做转换。
一般的类型基本如下，之后说到的矩阵也是类似的情况。

typedef struct _XMFLOAT2 {
    FLOAT x;
    FLOAT y;
} XMFLOAT2;

typedef struct _XMFLOAT3 {
    FLOAT x;
    FLOAT y;
    FLOAT z;
} XMFLOAT3;

typedef struct _XMFLOAT4 {
    FLOAT x;
    FLOAT y;
    FLOAT z;
    FLOAT w;
} XMFLOAT4;

XMFLOAT*类型与XMVECTOR类型的相互转换。

// Loads XMFLOAT2 into XMVECTOR
XMVECTOR XMLoadFloat2(CONST XMFLOAT2 *pSource);
// Loads XMFLOAT3 into XMVECTOR
XMVECTOR XMLoadFloat3(CONST XMFLOAT3 *pSource);
// Loads XMFLOAT4 into XMVECTOR
XMVECTOR XMLoadFloat4(CONST XMFLOAT4 *pSource);

// Loads 3-element UINT array into XMVECTOR
XMVECTOR XMLoadInt3(CONST UINT* pSource);
// Loads XMCOLOR into XMVECTOR
XMVECTOR XMLoadColor(CONST XMCOLOR *pSource);
// Loads XMBYTE4 into XMVECTOR
XMVECTOR XMLoadByte4(CONST XMBYTE4 *pSource);

// Loads XMVECTOR into XMFLOAT2
VOID XMStoreFloat2(XMFLOAT2 *pDestination, FXMVECTOR V);
// Loads XMVECTOR into XMFLOAT3
VOID XMStoreFloat3(XMFLOAT3 *pDestination, FXMVECTOR V);
// Loads XMVECTOR into XMFLOAT4
VOID XMStoreFloat4(XMFLOAT4 *pDestination, FXMVECTOR V);

// Loads XMVECTOR into 3 element UINT array
VOID XMStoreInt3(UINT* pDestination, FXMVECTOR V);
// Loads XMVECTOR into XMCOLOR
VOID XMStoreColor(XMCOLOR* pDestination, FXMVECTOR V);
// Loads XMVECTOR into XMBYTE4
VOID XMStoreByte4(XMBYTE4 *pDestination, FXMVECTOR V);

FLOAT XMVectorGetX(FXMVECTOR V);
FLOAT XMVectorGetY(FXMVECTOR V);
FLOAT XMVectorGetZ(FXMVECTOR V);
FLOAT XMVectorGetW(FXMVECTOR V);
XMVECTOR XMVectorSetX(FXMVECTOR V, FLOAT x);
XMVECTOR XMVectorSetY(FXMVECTOR V, FLOAT y);
XMVECTOR XMVectorSetZ(FXMVECTOR V, FLOAT z);
XMVECTOR XMVectorSetW(FXMVECTOR V, FLOAT w);

类型定义
// 32-bit Windows
typedef const XMVECTOR FXMVECTOR;
typedef const XMVECTOR& CXMVECTOR;
// 64-bit Windows
typedef const XMVECTOR& FXMVECTOR;
typedef const XMVECTOR& CXMVECTOR;

有很多方法都已经被DirectXMath高效的实现了，要善用高效的方法。

Matrix Algebra

矩阵的情况跟向量的一样，简单说一下常用的矩阵的性质：

\begin{aligned} 1. (A + B)^{T} = A^{T} + B^{T} \\ 2. (c A)^{T} = c A^{T} \\ 3. (A B)^{T} = B^{T} A^{T} \\ 4. (A^{T})^{T} = A \\ 5. (A^{- 1})^{T} = (A^{T})^{- 1} \end{aligned}

$\begin{align*} & 1. \qquad (A+B)^T=A^T+B^T\\ & 2. \qquad (cA)^T = cA^T\\ & 3. \qquad (AB)^T = B^TA^T\\ & 4. \qquad (A^T)^T = A\\ & 5. \qquad (A^{-1})^T = (A^T)^{-1} \end{align*}$

行列式

矩阵的行列式在计算逆矩阵的时候会用到，百度百科对行列的简单介绍，更多的看wiki，行列式返回一个实数
3阶行列式计算

伴随矩阵

$A^*$ 设矩阵 $A=(a_{ij})_{n \times n}$ ，将矩阵A的元素 $a_{ij}$ 所在的第i行第j列元素划去后，剩余的 $(n-1)^2$ 个元素按原来的排列顺序组成的n-1阶矩阵所确定的行列式称为元素 $a_{ij}$ 的余子式，记为 $M_{ij}$ ，称 $A_{ij}=(-1)^{i+j}M_{ij}$ 为元素 $a_{ij}$ 的代数余子式。
方阵的 $A=(a_{ij})_{n \times n}$ 各元素的代数余子式 $A_{ij}$ 所构成的如下矩阵 $A^*$ ：

\begin{matrix} A_{11} & A_{21} & \dots & A_{n 1} \\ A_{12} & A_{22} & \dots & x \\ ⋮ & ⋮ & ⋮ \\ A_{1 n} & A_{2 n} & \dots & A_{n n} \end{matrix}

$\begin{matrix} A_{11} & A_{21} & \cdots & A_{n1}\\ A_{12} & A_{22} & \cdots & x\\ \vdots & \vdots & & \vdots\\ A_{1n} & A_{2n} & \cdots & A_{nn} \end{matrix}$

该矩阵 $A^*$ 称为矩阵A的伴随矩阵。

逆矩阵

A^{- 1} = \frac{A^{*}}{det A}

$A^{-1}=\frac{A^*}{\det A}$
当然最基础还是矩阵与逆矩阵的乘机为单位矩阵

XNA类型跟Vector非常类似

TRANSFORMATIONS

下面说到的矩阵变换表示都是对向量右乘一个矩阵，对向量 $u=(x,y,z)$ 执行矩阵 $A$ 的变换

\begin{matrix} (1) & \begin{aligned} τ (u) & = τ (x i + y j + z k) \\ = x τ (i) + y τ (j) + z τ (k) \\ = u A \\ = [\begin{matrix} x, & y, & z \end{matrix}] [\begin{matrix} \leftarrow τ (i) \to \\ \leftarrow τ (j) \to \\ \leftarrow τ (k) \to \end{matrix}] \end{aligned} \end{matrix}

$\begin{align*} \tau(u) &=\tau(xi+yj+zk)\\ &=x\tau(i)+y\tau(j)+z\tau(k)\\ &=uA\\ &= \begin{bmatrix} x, & y, & z \end{bmatrix} \begin{bmatrix} \leftarrow \tau(i) \rightarrow\\ \leftarrow \tau(j) \rightarrow\\ \leftarrow \tau(k) \rightarrow \end{bmatrix} \end{align*} \tag 1$

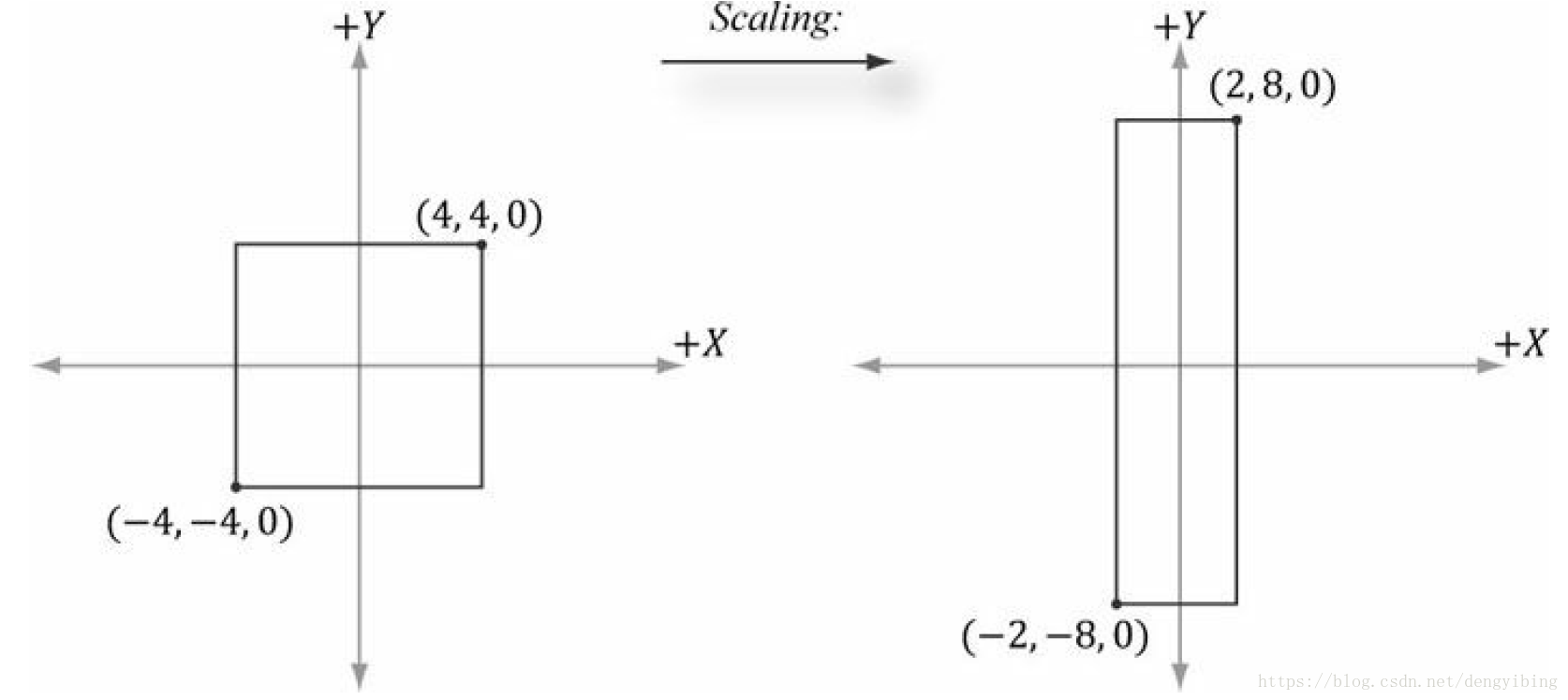
缩放

矩阵表示，沿着 $x,y,z$ 轴旋转的缩放系数分别是 $s_{x},s_{y},s_{z}$

S = [\begin{matrix} s_{x} & 0 & 0 \\ 0 & s_{y} & 0 \\ 0 & 0 & s_{z} \end{matrix}]

$S = \begin{bmatrix} s_{x} & 0 & 0 \\ 0 & s_{y} & 0\\ 0 & 0 & s_{z} \end{bmatrix}$

其逆矩阵为

S^{- 1} = [\begin{matrix} 1 / s_{x} & 0 & 0 \\ 0 & 1 / s_{y} & 0 \\ 0 & 0 & 1 / s_{z} \end{matrix}]

$S^{-1} = \begin{bmatrix} 1/s_{x} & 0 & 0 \\ 0 & 1/s_{y} & 0\\ 0 & 0 & 1/s_{z} \end{bmatrix}$

例子
Scale by one-half units on the x-axis

旋转

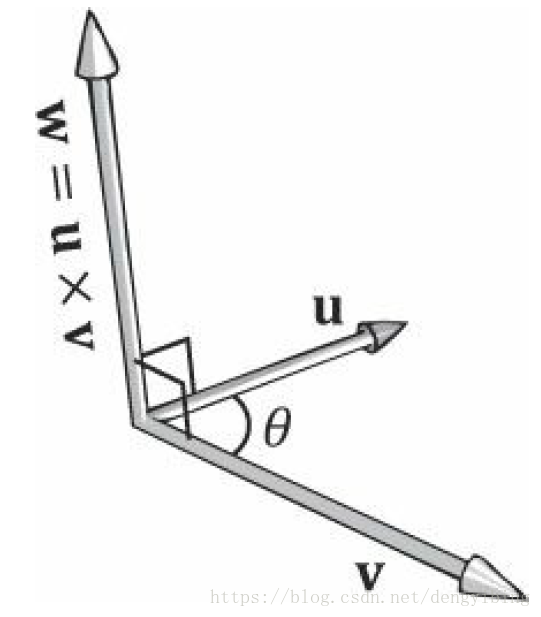
绕任意轴旋转，比如绕轴 $n$ 旋转，假设为单位长度。此时向量 v 要绕着轴 n 旋转 $\theta$ 角度，得到 $R_{n}(v)$ 。把v分解为平行于n的部分 $proj_n(v)$ 和垂直于n的部分. $v_{\perp}=perp_n(v)=v-proj_n(v)$
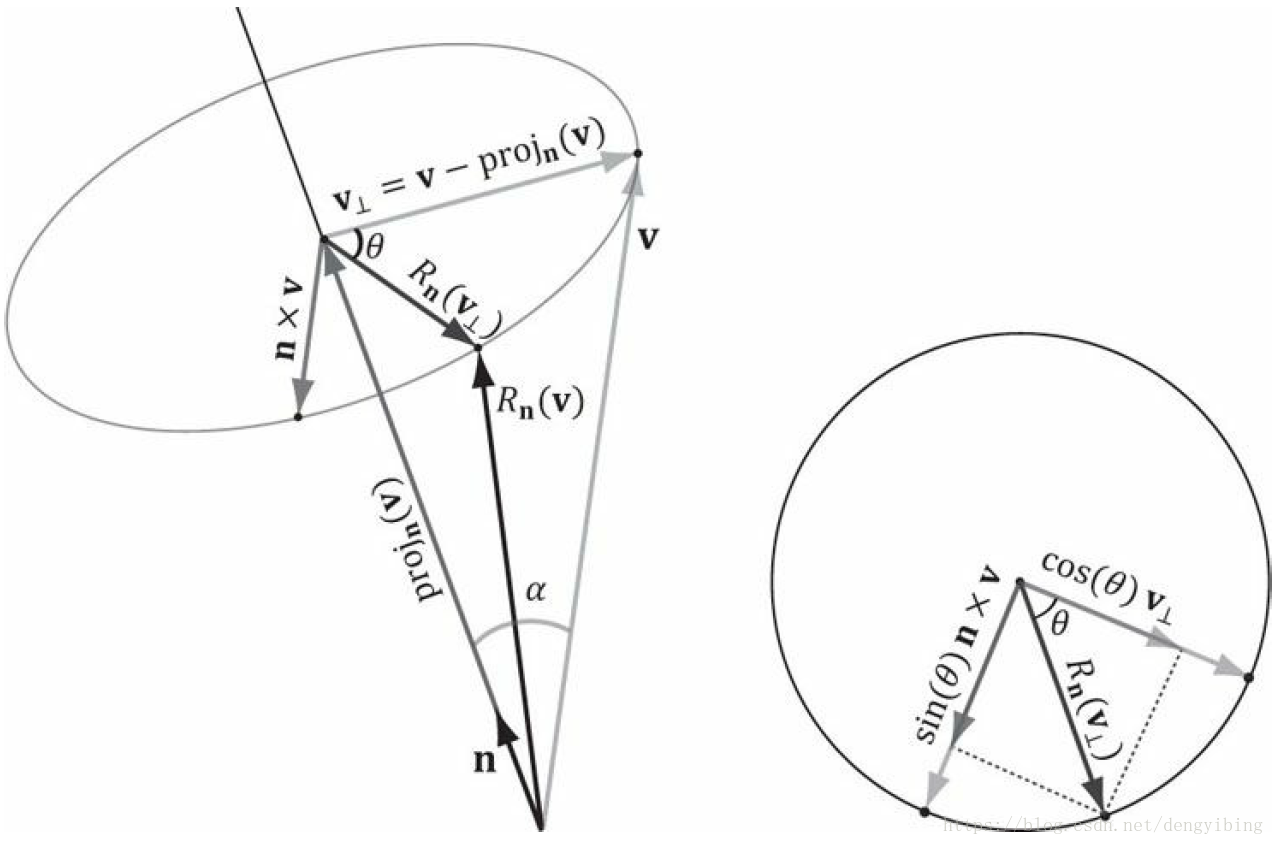
The geometry of rotation about a vector n
由上图可以得到

\begin{aligned} R_{n} (v) & = p r o j_{n} (v) + R_{n} (v_{⊥}) \\ = (n \cdot v) n + \cos θ v_{⊥} + \sin θ (n \times v) \\ = (n \cdot v) n + \cos θ (v - (n \cdot v) n) + \sin θ (n \times v) \\ = \cos θ v + (1 - \cos θ) (n \cdot v) n + \sin θ (n \times v) \end{aligned}

$\begin{align*} R_n(v) & = proj_n(v)+R_n(v_{\perp})\\ & = (n \cdot v)n+\cos\theta v_{\perp}+\sin \theta (n \times v)\\ & = (n \cdot v)n+\cos\theta(v-(n \cdot v)n)+\sin \theta(n \times v)\\ & = \cos \theta v+(1-\cos \theta)(n \cdot v)n+\sin\theta(n \times v) \end{align*}$
把上面公式写成跟公式(1)类似的，对向量

(x, y, z)

$(x,y,z)$ 做旋转，矩阵形式如下，其中

c = \cos θ, s = \sin θ

$c=\cos\theta, s=\sin\theta$ ：

R_{n} = [\begin{matrix} c + (1 - c) x^{2} & (1 - c) x y + s z & (1 - c) x z - s y \\ (1 - c) x y - s z & c + (1 - c) y^{2} & (1 - c) y z + s x \\ (1 - c) x z + s y & (1 - c) y z - s x & c + (1 - c) z^{2} \end{matrix}]

$R_n = \begin{bmatrix} c+(1-c)x^2 & (1-c)xy+sz & (1-c)xz-sy\\ (1-c)xy-sz & c+(1-c)y^2 & (1-c)yz+sx\\ (1-c)xz+sy & (1-c)yz-sx & c+(1-c)z^2 \end{bmatrix}$
而且该矩阵为正交矩阵，正交矩阵的逆为其转置

R_{n}^{- 1} = R_{n}^{T} = [\begin{matrix} c + (1 - c) x^{2} & (1 - c) x y - s z & (1 - c) x z + s y \\ (1 - c) x y + s z & c + (1 - c) y^{2} & (1 - c) y z - s x \\ (1 - c) x z - s y & (1 - c) y z + s x & c + (1 - c) z^{2} \end{matrix}]

$R_n^{-1} = R_n^T = \begin{bmatrix} c+(1-c)x^2 & (1-c)xy-sz & (1-c)xz+sy\\ (1-c)xy+sz & c+(1-c)y^2 & (1-c)yz-sx\\ (1-c)xz-sy & (1-c)yz+sx & c+(1-c)z^2 \end{bmatrix}$

则作为特殊情况，绕 $x,y,z$ 轴 $(n=(1,0,0),n=(0,1,0),n=(0,0,1))$ 分别旋转的旋转矩阵分别如下

R_{x} = [\begin{matrix} 1 & 0 & 0 & 0 \\ 0 & \cos θ & \sin θ & 0 \\ 0 & - \sin θ & \cos θ & 0 \\ 0 & 0 & 0 & 1 \end{matrix}], R_{y} = [\begin{matrix} \cos θ & 0 & - \sin θ & 0 \\ 0 & 1 & 0 & 0 \\ \sin θ & 0 & \cos θ & 0 \\ 0 & 0 & 0 & 1 \end{matrix}], R_{z} = [\begin{matrix} \cos θ & \sin θ & 0 & 0 \\ - \sin θ & \cos θ & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix}]

$R_{x} = \begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & \cos\theta & \sin \theta & 0\\ 0 & -\sin \theta & \cos \theta & 0\\ 0 & 0 & 0 & 1 \end{bmatrix} ,\\ R_{y} = \begin{bmatrix} \cos \theta & 0 & -\sin \theta & 0\\ 0 & 1 & 0 & 0\\ \sin \theta & 0 & \cos \theta & 0\\ 0 & 0 & 0 & 1 \end{bmatrix} ,\\ R_{z} = \begin{bmatrix} \cos \theta & \sin \theta & 0 & 0\\ -\sin \theta & \cos\theta & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{bmatrix}$

仿射变换

仿射变换就是带偏移的线性变换，可以表示为如下：

\begin{aligned} α (u) & = u A + b \\ = [\begin{matrix} x, & y, & z \end{matrix}] [\begin{matrix} A_{11} & A_{12} & A_{13} \\ A_{21} & A_{22} & A_{23} \\ A_{31} & A_{32} & A_{33} \end{matrix}] + [\begin{matrix} b_{x} & b_{y} & b_{z} \end{matrix}] \\ = [\begin{matrix} x^{'}, & y^{'}, & z^{'} \end{matrix}] \end{aligned}

$\begin{align*} \alpha(u) &=uA+b\\ &= \begin{bmatrix} x, & y, & z \end{bmatrix} \begin{bmatrix} A_{11} & A_{12} & A_{13}\\ A_{21} & A_{22} & A_{23}\\ A_{31} & A_{32} & A_{33} \end{bmatrix} + \begin{bmatrix} b_x & b_y & b_z \end{bmatrix}\\ &= \begin{bmatrix} x^\prime, & y^\prime, & z^\prime \end{bmatrix} \end{align*}$
但是上面的写法很麻烦，所以用4维向量和矩阵计算将会更简洁高效，因为GPU本身就是并行运算能力超强。
所以上面改写为如下：

[\begin{matrix} x, & y, & z, & 1 \end{matrix}] [\begin{matrix} A_{11} & A_{12} & A_{13} & 0 \\ A_{21} & A_{22} & A_{23} & 0 \\ A_{31} & A_{32} & A_{33} & 0 \\ b_{x} & b_{y} & b_{z} & 1 \end{matrix}] = [\begin{matrix} x^{'}, & y^{'}, & z^{'}, & 1 \end{matrix}]

$\begin{bmatrix} x, & y, & z, & 1 \end{bmatrix} \begin{bmatrix} A_{11} & A_{12} & A_{13} & 0\\ A_{21} & A_{22} & A_{23} & 0\\ A_{31} & A_{32} & A_{33} & 0\\ b_x & b_y & b_z & 1 \end{bmatrix} =\begin{bmatrix} x^\prime, & y^\prime, & z^\prime, & 1 \end{bmatrix}$
上面是对点的变换，所以把最后一项设置为1，因为点有偏移；但是，对于向量来说，是没有偏移这个概念的，所以最后一项设置为0。这样的4维向量和矩阵才是图形学中常用的形式。

移动

转移矩阵可以写为

T = [\begin{matrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ b_{x} & b_{y} & b_{z} & 1 \end{matrix}]

$T = \begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ b_x & b_y & b_z & 1 \end{bmatrix}$
其逆矩阵

T^{- 1} = [\begin{matrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ - b_{x} & - b_{y} & - b_{z} & 1 \end{matrix}]

$T^{-1} = \begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ -b_x & -b_y & -b_z & 1 \end{bmatrix}$

对缩放和旋转的仿射矩阵

S = [\begin{matrix} s_{x} & 0 & 0 & 0 \\ 0 & s_{y} & 0 & 0 \\ 0 & 0 & s_{z} & 0 \\ 0 & 0 & 0 & 1 \end{matrix}] R_{n} = [\begin{matrix} c + (1 - c) x^{2} & (1 - c) x y + s z & (1 - c) x z - s y & 0 \\ (1 - c) x y - s z & c + (1 - c) y^{2} & (1 - c) y z + s x & 0 \\ (1 - c) x z + s y & (1 - c) y z - s x & c + (1 - c) z^{2} & 0 \\ 0 & 0 & 0 & 1 \end{matrix}]

$S = \begin{bmatrix} s_x & 0 & 0 & 0\\ 0 & s_y & 0 & 0\\ 0 & 0 & s_z & 0\\ 0 & 0 & 0 & 1 \end{bmatrix} \\ R_n = \begin{bmatrix} c+(1-c)x^2 & (1-c)xy+sz & (1-c)xz-sy & 0\\ (1-c)xy-sz & c+(1-c)y^2 & (1-c)yz+sx & 0\\ (1-c)xz+sy & (1-c)yz-sx & c+(1-c)z^2 & 0\\ 0 & 0 & 0 & 1 \end{bmatrix}$

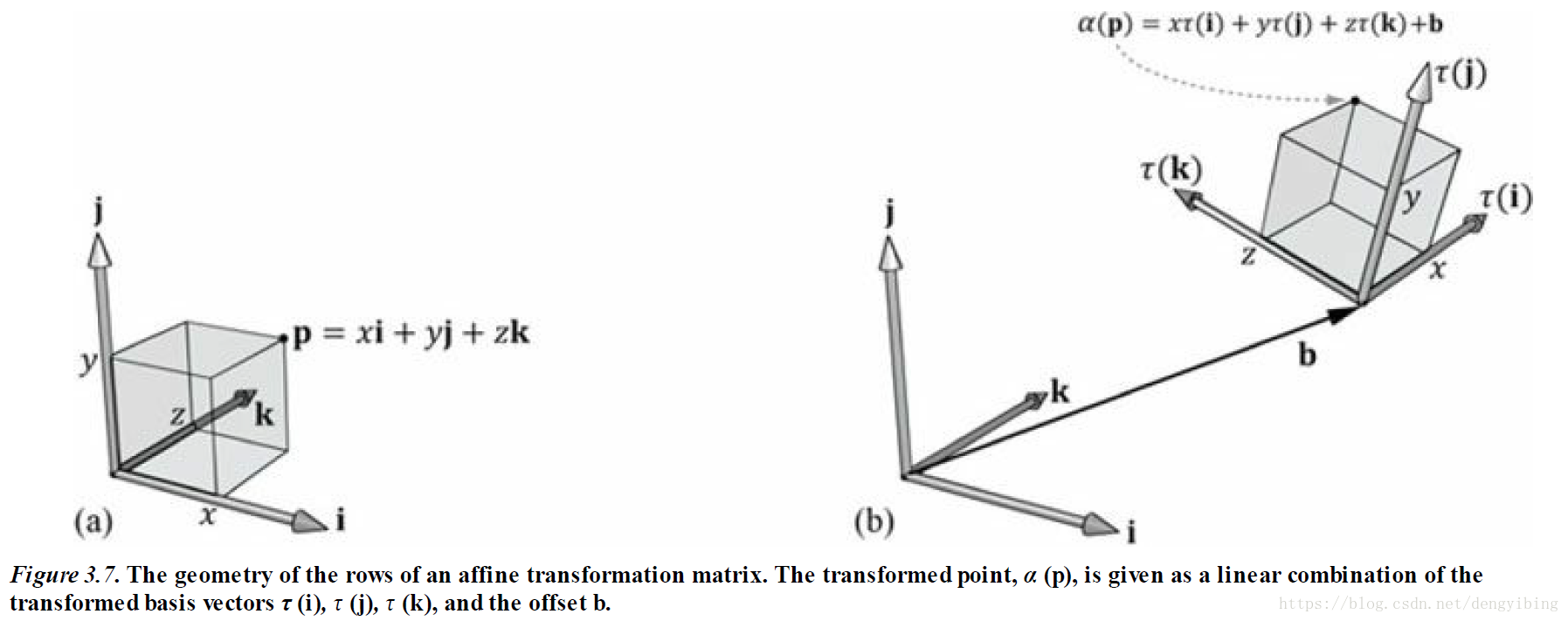
仿射变换矩阵的几何解释

上面介绍的仿射变换就是旋转/缩放，移动

用公式表示 $a(x,y,z)=\tau(x,y,z)+b=x\tau(i)+y\tau(j)+z\tau(k)+b$ 如下（其中对于顶点 $w=1$ ，对于向量 $w=0$ ）:

[\begin{matrix} x, & y, & z, & w \end{matrix}] [\begin{matrix} \leftarrow τ (i) \to \\ \leftarrow τ (j) \to \\ \leftarrow τ (k) \to \\ \leftarrow b \to \end{matrix}] = [\begin{matrix} x^{'}, & y^{'}, & z^{'}, & w \end{matrix}]

$\begin{bmatrix} x, & y, & z, & w \end{bmatrix} \begin{bmatrix} \leftarrow \tau(i) \rightarrow\\ \leftarrow \tau(j) \rightarrow\\ \leftarrow \tau(k) \rightarrow\\ \leftarrow b \rightarrow \end{bmatrix} =\begin{bmatrix} x^\prime, & y^\prime, & z^\prime, & w \end{bmatrix}$

仿射变换矩阵解释图例

因为矩阵有结合律但没有交换律，所以矩阵相乘最后作用于对象的顺序非常关键，是先旋转再平移与先平移再旋转有很大差别。

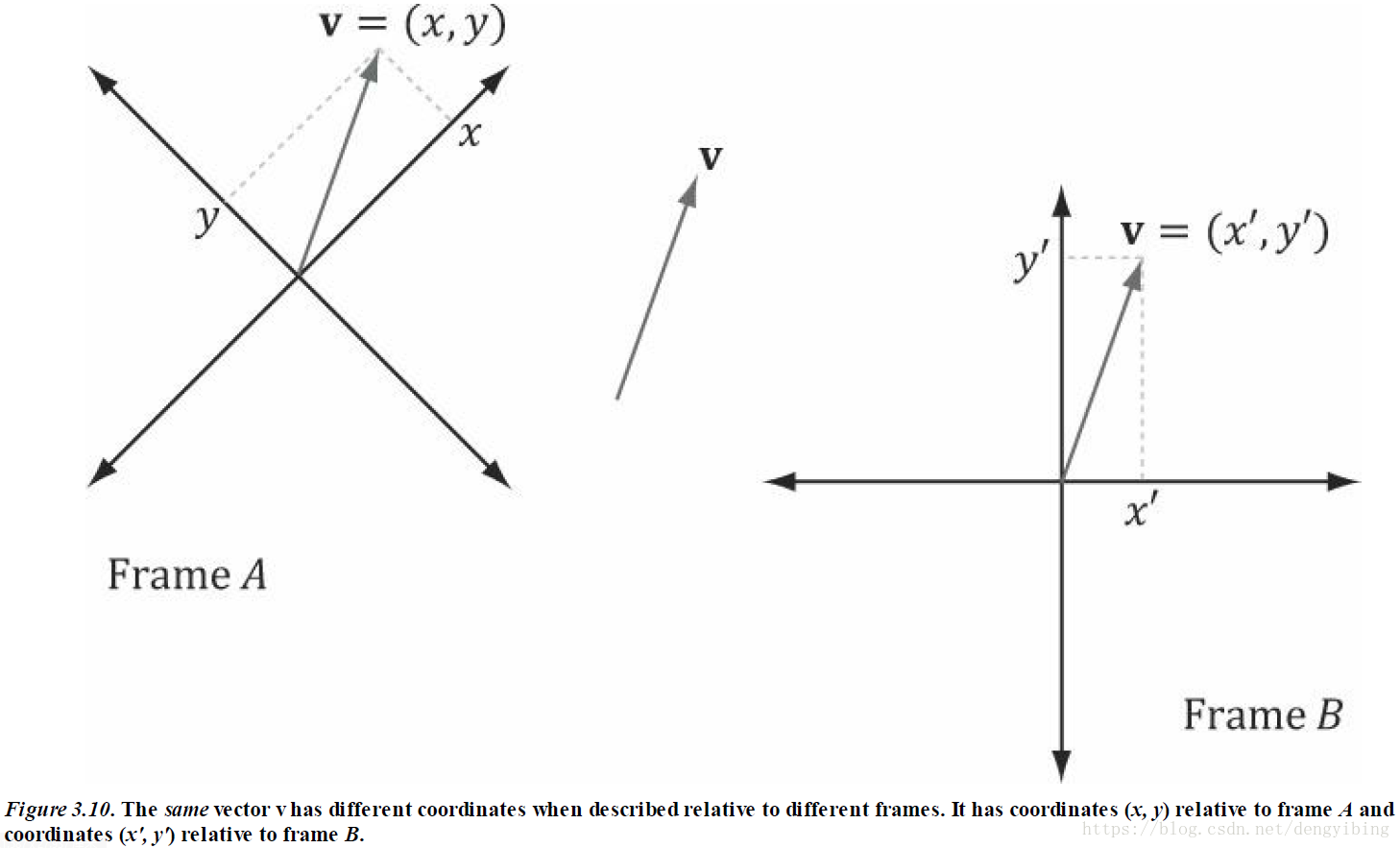
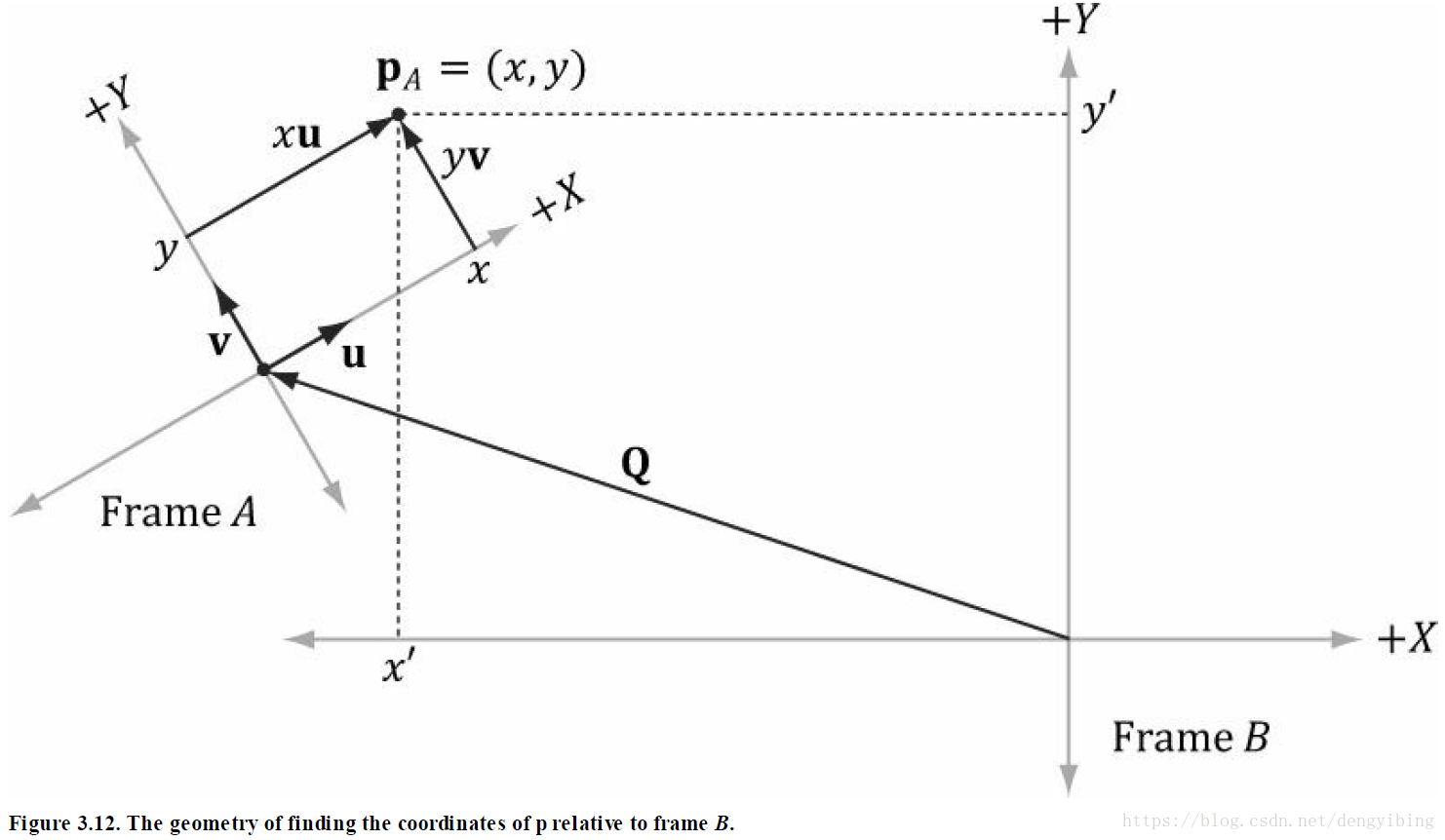
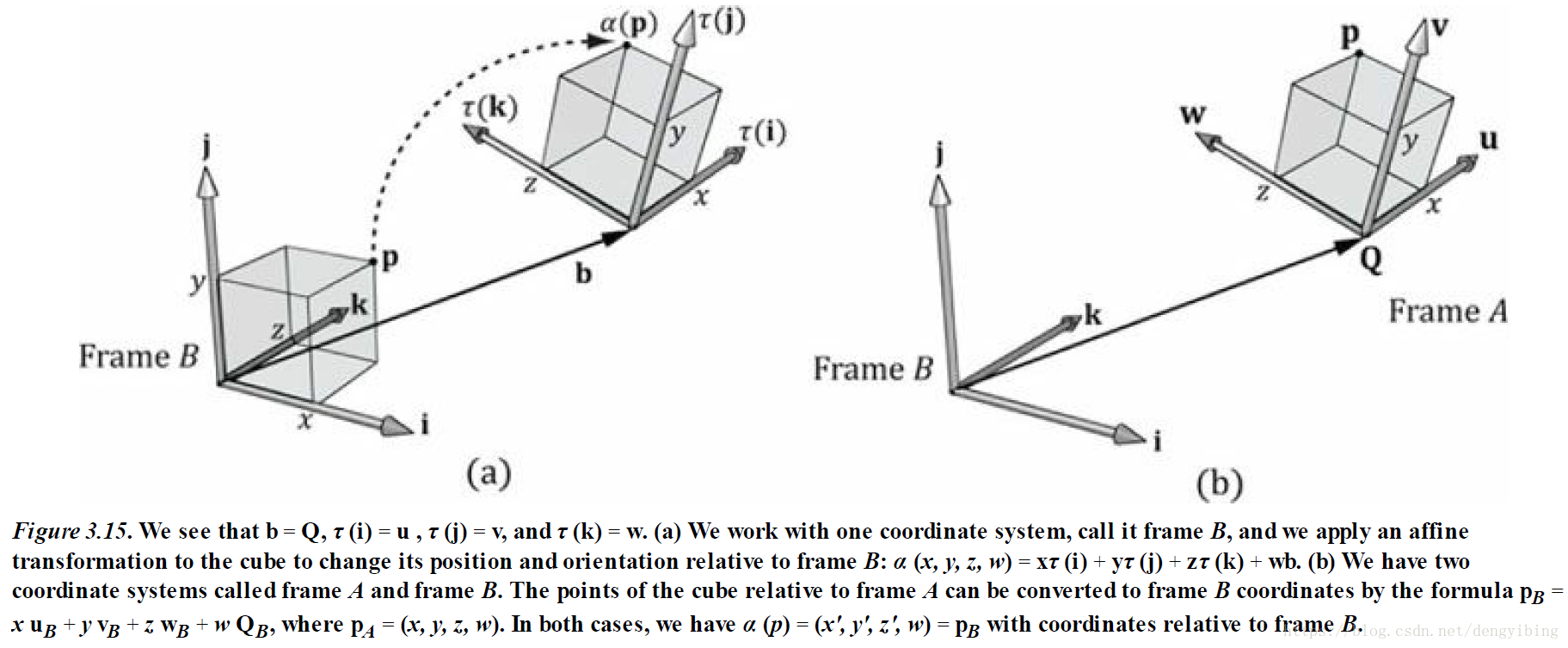
坐标系变换

摄氏度与华氏度表示相同的问题时数字大小是不一样的，不同的基底（坐标系）之间的转换得到相同坐标不同的表示。
对基底的变换与做顶点和向量的变换不同，刚好是完全相反的。
向量在不同基底下的表示

简单的坐标系统变换

顶点和向量的坐标转换，将坐标系A下的顶点表示转换为坐标系B下的顶点表示。

(x^{'}, y^{'}, z^{'}, w) = x u_{B} + y v_{B} + z w_{B} + w Q_{B}

$(x^\prime, y^\prime, z^\prime, w) = xu_B+yv_B+zw_B+wQ_B$
跟之前介绍的一样，

w = 0

$w=0$ 表示对向量的坐标系变换，

w = 1

$w=1$ 表示对顶点的变换。

上式写成矩阵形式

\begin{aligned} [\begin{matrix} x^{'}, y^{'}, z^{'}, w \end{matrix}] & = [\begin{matrix} x, y, z, w \end{matrix}] [\begin{matrix} \leftarrow u_{B} \to \\ \leftarrow v_{B} \to \\ \leftarrow w_{B} \to \\ \leftarrow Q_{B} \to \end{matrix}] \\ = [\begin{matrix} x, y, z, w \end{matrix}] [\begin{matrix} u_{x} & u_{y} & u_{z} & 0 \\ v_{x} & v_{y} & v_{z} & 0 \\ w_{x} & w_{y} & w_{z} & 0 \\ Q_{x} & Q_{y} & Q_{z} & 1 \end{matrix}] \\ = x u_{B} + y v_{B} + z w_{B} + w Q_{B} \end{aligned}

$\begin{align*} \begin{bmatrix} x^\prime, y^\prime, z^\prime, w \end{bmatrix} & = \begin{bmatrix} x, y, z, w \end{bmatrix} \begin{bmatrix} \leftarrow u_B \rightarrow\\ \leftarrow v_B \rightarrow\\ \leftarrow w_B \rightarrow\\ \leftarrow Q_B \rightarrow \end{bmatrix}\\ & = \begin{bmatrix} x, y, z, w \end{bmatrix} \begin{bmatrix} u_x & u_y & u_z & 0\\ v_x & v_y & v_z & 0\\ w_x & w_y & w_z & 0\\ Q_x & Q_y & Q_z & 1 \end{bmatrix}\\ & = xu_B+yv_B+zw_B+wQ_B \end{align*}$
其中

Q_{B} = (Q_{x}, Q_{y}, Q_{z}, 1), u_{B} = (u_{x}, u_{y}, u_{z}, 0), v_{B} = (v_{x}, v_{y}, v_{z}, 0), w_{B} = (w_{x}, w_{y}, w_{z}, 0)

$Q_B=(Q_x,Q_y,Q_z,1), u_B=(u_x, u_y, u_z, 0), v_B=(v_x, v_y, v_z, 0), w_B=(w_x, w_y, w_z, 0)$ 分别表示原点以及齐次坐标系A相对于齐次坐标系B的轴。

给个例子，如下图：
坐标系A相对于坐标系B的轴

比较转换矩阵和坐标系变换矩阵

TRANSFORMATION MATRIX VERSUS CHANGE OF COORDINATE MATRIX

其实两者数学上是等价的，不同之处在于理解和解释转换的方式有所不同
不同的理解方式

XNA的实现

在XNA中，所有这些转换都已经实现了

// Constructs a scaling matrix:
XMMATRIX XMMatrixScaling(
    FLOAT ScaleX,
    FLOAT ScaleY,
    FLOAT ScaleZ); // Scaling factors

// Constructs a scaling matrix from components in vector:
XMMATR IX XMMatrixScalingFromVector(
    FXMVECTOR Scale); // Scaling factors (sx , sy , sz)

// Constructs a x-axis rotation matrix : Rx
XMMATRIX XMMatrixRotationX(
    FLOAT Angle); // Clockwise angle θ to rotate

// Constructs a y-axis rotation matrix : Ry
XMMATRIX XMMatrixRotationY(
    FLOAT Angle); // Clockwise angle θ to rotate

// Constructs a z-axis rotation matrix : Rz
XMMATRIX XMMatrixRotationZ(
    FLOAT Angle); // Clockwise angle θ to rotate

// Constructs an arbitrary axis rotation matrix : Rn
XMMATRIX XMMatrixRotationAxis(
    FXMVECTOR Axis, // Axis n to rotate about
    FLOAT Angle); // Clockwise angle θ to rotate

//Constructs a translation matrix:
XMMATRIX XMMatrixTranslation(
    FLOAT OffsetX,
    FLOAT OffsetY,
    FLOAT OffsetZ); // Translation factors

//Constructs a translation matrix from components in a vector:
XMMATRIX XMMatrixTranslationFromVector(
    FXMVECTOR Offset); // Translation factors (tx , ty ,tz)

// Computes the vector-matrix product vM:
XMVECTOR XMVector3Transform(
    FXMVECTOR V, // Input v
    CXMMATRIX M); // Input M

// Computes the vector-matrix product vM where vw = 1 for   transforming points:
XMVECTOR XMVector3TransformCoord(
    FXMVECTOR V, // Input v
    CXMMATRIX M); // Input M

// Computes the vector-matrix product vM where vw = 0 for               transforming vectors:
XMVECTOR XMVector3TransformNormal(
    FXMVECTOR V, // Input v
    CXMMATRIX M); // Input M