集训终于结束了,这个成绩挺出乎我的预料。不论牛客还是杭电,正常发挥20多名,发挥好了能打到十几名。包括昨天 CCPC 预选赛打了第十名(zcq yyds),给我一种选对赛站能出线的感觉?虽然打出来的成绩是以前没想到的,但是这 20 场比赛一场一场打下来以后,我也深刻体会到有很多地方还有不足,而且训练赛三人三机也和正式比赛不一样。
继续加油
目录
contest2
A - Arithmetic Progression

第一步观察就没看出来…
首先,b 的公差一定是 g c d i = 1 n − 1 { b i + 1 − b i } gcd_{i=1}^{n-1}\{b_{i + 1} - b_i\} gcdi=1n−1{ bi+1−bi}。因此相当于判断 ( r − l + 1 ) ⋅ g c d i = 1 n − 1 { b i + 1 − b i } − m a x { b i } + m i n { b i } (r - l +1) · gcd_{i=1}^{n-1}\{b_{i + 1} - b_i\} - max\{b_i\} + min\{b_i\} (r−l+1)⋅gcdi=1n−1{ bi+1−bi}−max{ bi}+min{ bi} 是不是等于 0。
枚举右端点,用线段树维护左端点。max 和 min 用单调栈处理即可。注意到
- 对于一个右端点,gcd 不同的左端点至多 log 段。
- 对于一个左端点,右端点右移的过程中 gcd 最多变化 log 次。
因此右端点移动的时候,对于 gcd 不变的左端点,由于 1,可以进行 log 段区间加;对于 gcd 变化的左端点,由于 2,暴力单点修改即可。
注意到,需要单点修改的左端点一定是一个后缀。用一个栈维护一下 log 段 gcd 的右端点即可。
contest3
G - Yu Ling(Ling YueZheng) and Colorful Tree

颜色范围 [1, n]。
容易想到构建 n 棵树,第 i 棵树上存放颜色是 i 的倍数的点的信息。因为保证颜色两两不重复,因此总点数是 nlogn 的。之后,对于某个询问,相当于在某一刻线段树上查询颜色在某个范围内的,某个点的最近祖先。注意到还有一个时间维度。
我考场上的做法是在最外围处理时间,抛开时间限制之后,离线,在线段树上 dfs,用 n 棵线段树维护当前点到根这条链上的信息即可(第 i
个叶子维护颜色 i 到根的距离,查询区间最大值),这部分是两个 log。至于外面时间的处理,可以 cdq + 虚树加一个 log,但我实在懒得写,因此用分块重构的方法,调整块大小为 n^0.8 左右复杂度和三个 log 差不多,但并没有通过此题。
考后看了逆十字的代码。注意到边权为正,因此“最近祖先”这个东西是可以二分的。因此问题转化成每次给某个点一个数,询问某个点向上的某条祖先链有没有范围在某个区间内的数。这是个二维信息,“祖先链”这一维可以在 dfs 序上用树状数组解决,另一维就是线段树了。于是这题就三个 log 解决了。
I - Kuriyama Mirai and Exclusive Or

感觉这是个神仙题啊… orz zcq
第一种操作好说,关键是第二种操作。
发现对于第 i 位,异或的序列一定是有 2^(i+1) 的周期。如果把原序列的每 2^(i+1) 个元素作为一行,那么会惊喜的发现所有 1 会形成 O(1) 个矩形!然后二维差分即可。
contest4
B - Sample Game

提供一个生成函数的做法。
令 f ( x ) = ∑ i = 0 ∞ P ( l e n > i ) x i f(x) = \sum_{i=0}^{\infty}P(len>i)x^i f(x)=∑i=0∞P(len>i)xi
根据题意,有 f ( x ) = ∏ i ( 1 + p i x + p i 2 x 2 + . . . ) = ∏ i 1 1 − p i x f(x) = \prod_i(1 + p_ix + p_i^2x^2 +...) = \prod_i\frac1{1-p_ix} f(x)=∏i(1+pix+pi2x2+...)=∏i1−pix1
答案是 ∑ i = 0 ∞ ( P ( l e n > i ) − P ( l e n > i + 1 ) ) i 2 = ∑ i = 1 ∞ P ( l e n > i ) ( i 2 − ( i − 1 ) 2 ) = ∑ i = 1 ∞ P ( l e n > i ) ( 2 i − 1 ) = \begin{aligned} & \sum_{i=0}^{\infty}(P(len>i)-P(len>i+1))i^2\\ = & \sum_{i=1}^{\infty}P(len>i)(i^2-(i-1)^2)\\ = & \sum_{i=1}^{\infty}P(len>i)(2i-1)\\ = & \end{aligned} ===i=0∑∞(P(len>i)−P(len>i+1))i2i=1∑∞P(len>i)(i2−(i−1)2)i=1∑∞P(len>i)(2i−1)
D - Rebuild Tree
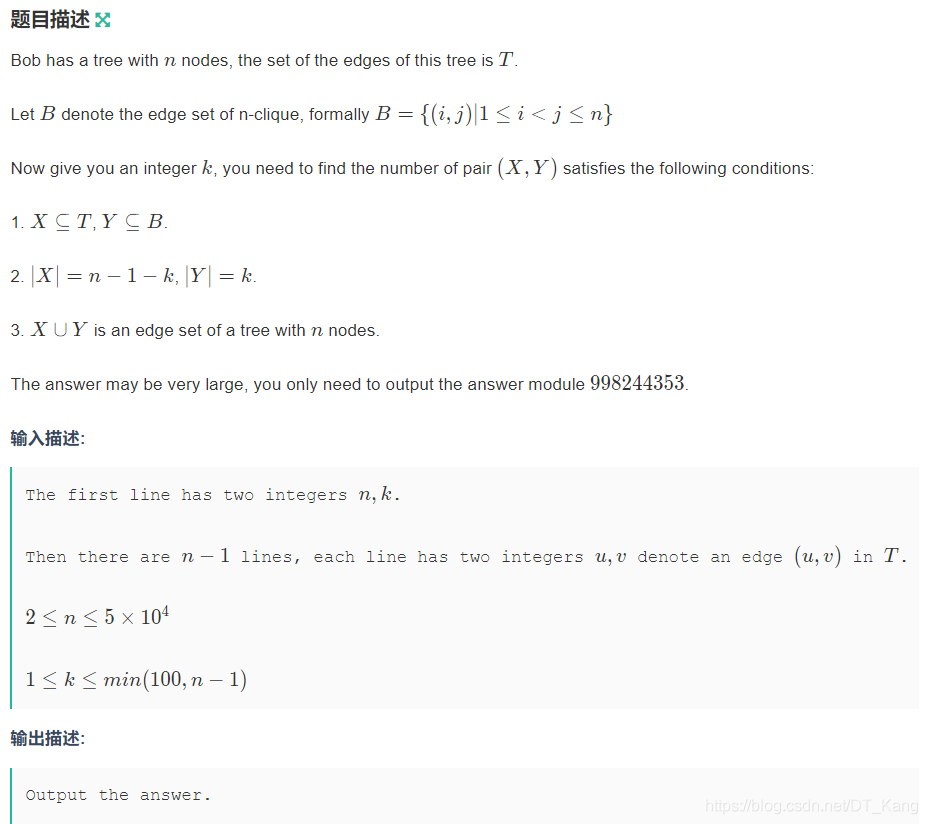
题意是给定一棵树,删除 k 条边,再任意加 k 条边使得它还是一棵树,求方案数。
回忆 prufer 序列,就是每次删除最小点把它的相邻点加入序列中。序列长度 n − 2 n-2 n−2,每个点在序列中出现 d i − 1 d_i - 1 di−1 次。因此 n 个点的树有 n n − 2 n^{n-2} nn−2 种。
容易发现,假设删完边以后剩下的联通快大小是 a 1 , . . . , a k a_1,...,a_k a1,...,ak,那么在这种删边方式下的方案数有 k k − 2 ∏ a i d i = ∑ p i a i n u m i ∏ i a i k^{k-2}\prod a_i^{d_i}=\sum_{p_i}a_i^{num_i}\prod_i a_i kk−2∏aidi=∑piainumi∏iai,其中最外面的 sigma 是枚举 k k − 2 k^{k-2} kk−2 种 prufer 序列, n u m i num_i numi 是第 i 个联通快在 prufer 序列中出现的次数。我到了这里就推不下去了。
其实这个式子还没有推到底。注意到 ∑ p i a i n u m i \sum_{p_i}a_i^{num_i} ∑piainumi 相当于有 k-2 个位置,每个位置可以选 a 1 , . . . , a k a_1,...,a_k a1,...,ak 中的任何一个,再相乘的方案数。因此它也就等于 ( ∑ a i ) k − 2 = n k − 2 (\sum a_i)^{k-2}=n^{k-2} (∑ai)k−2=nk−2。
因此,对于一种划分方式,只需要关注 ∏ a i \prod a_i ∏ai 的求法。这个东西的组合意义就是在每个联通快里选择恰好一个点的方案数,用树形 dp 可以非常轻松地解决。
contest5
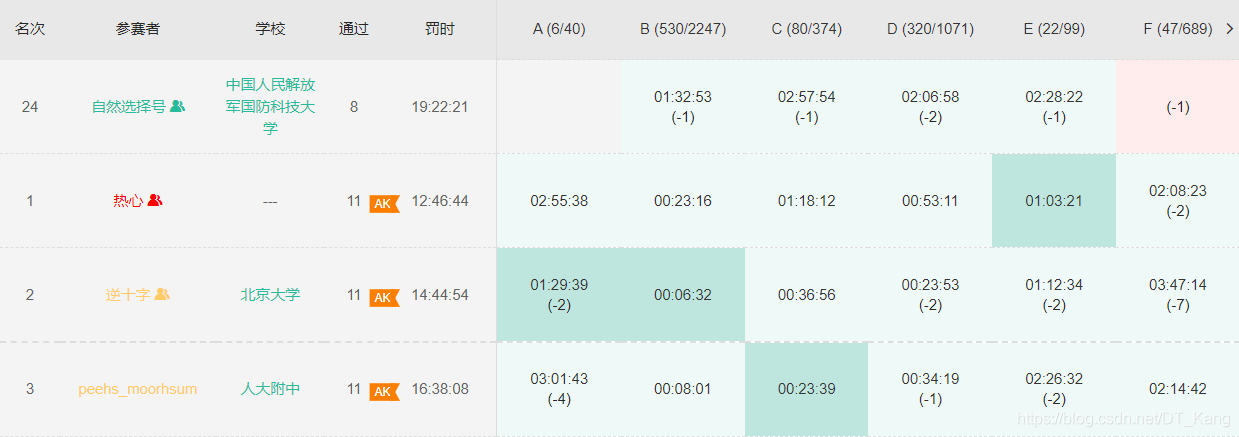
I - Interval Queries
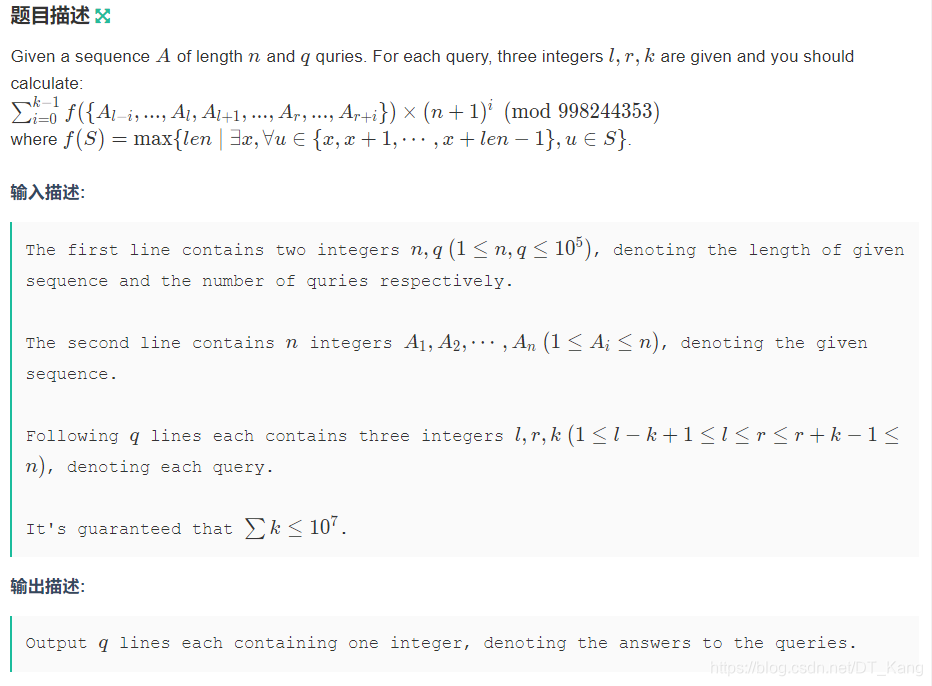
容易想到莫队。现在相当于一条线上 n 个点,每次连接相邻两个点,维护最长链。我一开始以为要并查集,但不支持撤销。后来发现每次合并肯定是链的两个端点相连,因此把链的信息维护在端电上即可。
当做回滚莫队板子题。
contest6
E - Growing Tree

重量平衡树维护括号序列,不多说了。
G - Hasse Diagram
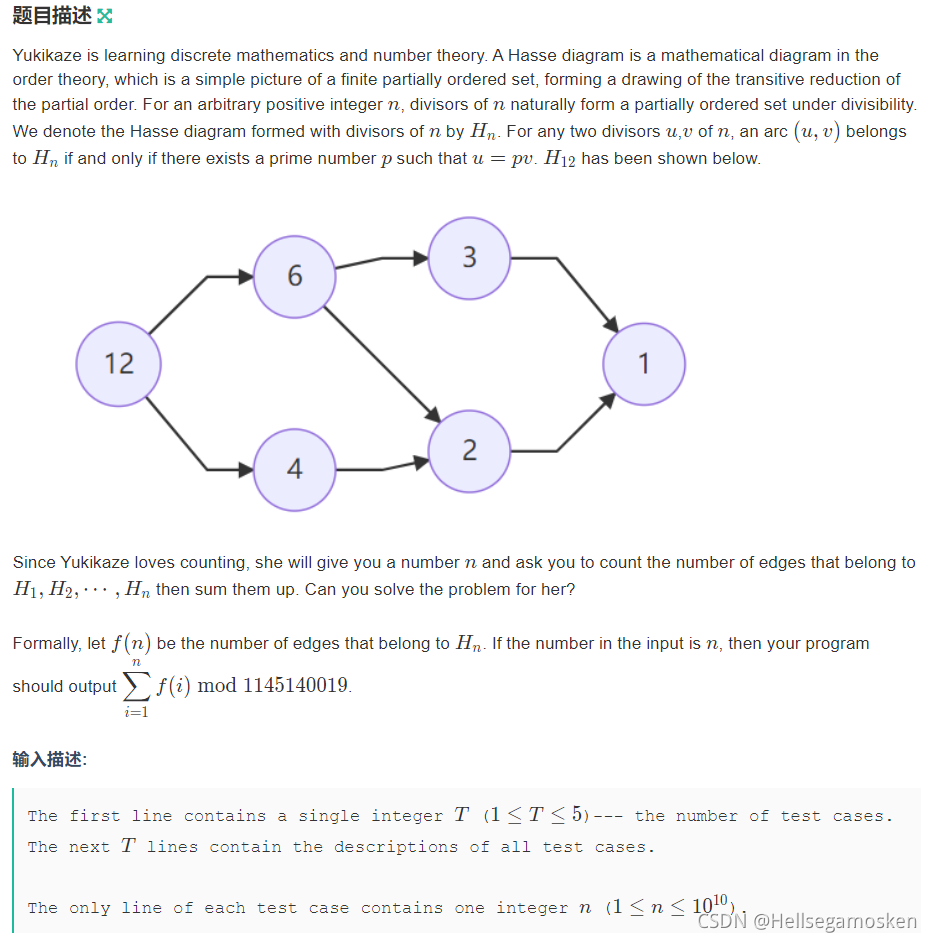
我的做法是:考虑某条边 i ∗ p → p i * p \rightarrow p i∗p→p 在 f ( 1 ) , . . . , f ( n ) f(1),..., f(n) f(1),...,f(n) 中一共出现了多少次。显然对于所有 ( i ∗ p ) ∣ n (i * p) | n (i∗p)∣n 的 n 都有这条边,因此答案是 ∑ i = 1 n ∑ p ⌊ n i p ⌋ = ∑ i = 1 n f ( n / i ) , f ( m ) = ∑ p ⌊ m / p ⌋ \sum_{i=1}^n\sum_p \lfloor\frac{n}{ip}\rfloor=\sum_{i=1}^nf(n/i),f(m)=\sum_p\lfloor m/p\rfloor ∑i=1n∑p⌊ipn⌋=∑i=1nf(n/i),f(m)=∑p⌊m/p⌋,整除分块后我们只需计算区间质数个数即可,这个用 min25 筛即可解决。但是复杂度不在 min25,而在于两次整除分块的 n 0.75 n^{0.75} n0.75。然后考场上我就卡不过去了。冷静下来以后发现可以算出 m 较小时的 f(m),这样就不需要每次对 m 分块,可以通过此题。
实际上,考虑 n = ∏ p e n=\prod p^e n=∏pe,枚举任意一个质因子 p 即可得到 f ( n ) = ( e + 1 ) f ( n / p e ) + e d ( n / p e ) f(n)=(e+1)f(n/p^e)+ed(n/p^e) f(n)=(e+1)f(n/pe)+ed(n/pe)。这正是 min25 筛允许的形式,拿板子改一改就行了。
contest7
B - xay loves monotonicity
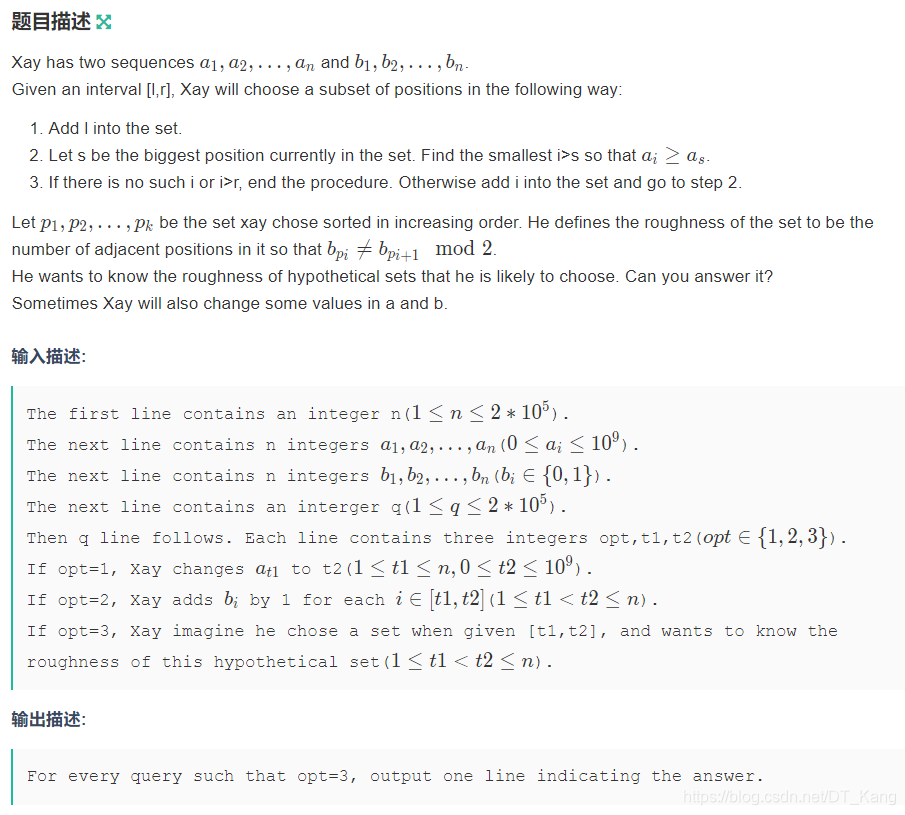
其实这是个稍加魔改的的线段树维护单调栈。但考场上把算答案对 b 的限制的那个 mod 2 的位置理解错了。实际上对 b 的修改没啥卵用。
有人用分块重构过了这个题,我看了下复杂度应该就是 n n log n n\sqrt{n\log n} nnlogn ,我是没想到的。
J - xay loves Floyd
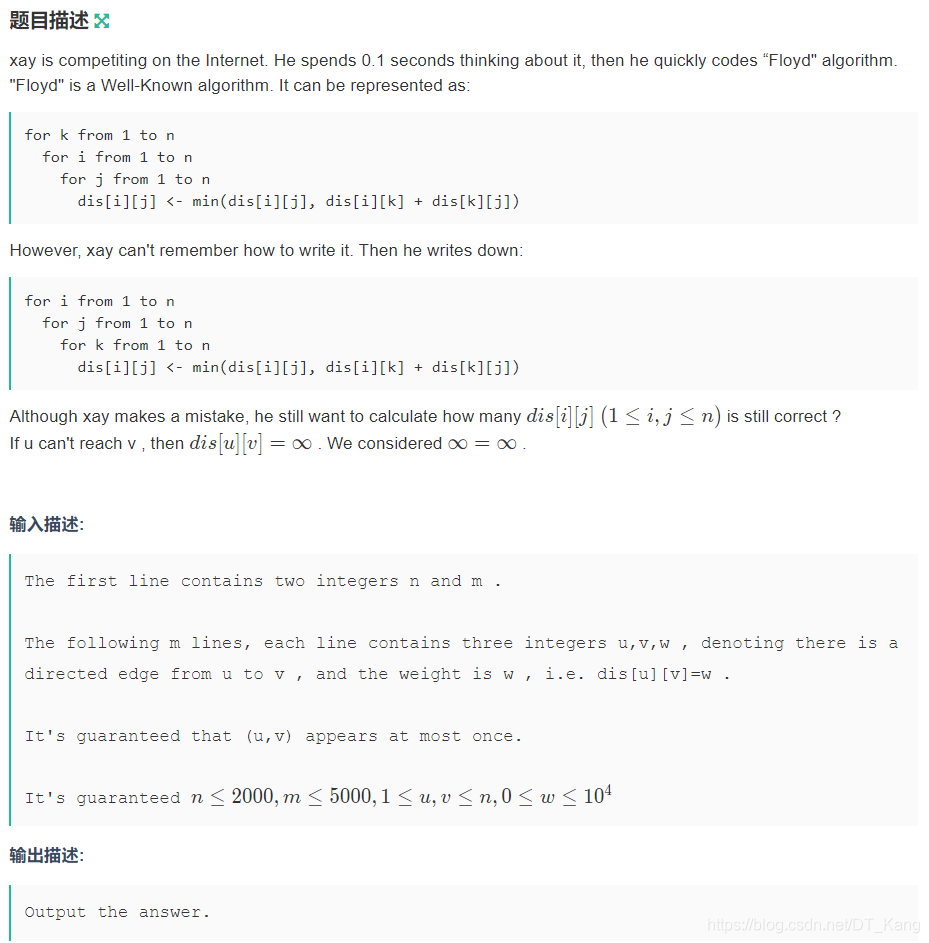
为啥老是想不到 bitset 啊… 明明是个简单题。
显然可以跑 n 遍最短路,然后就知道初始的哪些 (i, j) 满足 w(i, j) 已经是最短路了,记为 can[i][j]。然后模拟伪 Floyd,我们只需要关心过程中的 can[i][j] 即可,而不需要实际算出任意两点的最短路数值。而 can[i][j] 为真,当且仅当外层枚举到 i 的时候存在 z 使得 can[i][z] = 1 && can[z][j] = 1 && z ∈ pot[i][j]。其中 pot[i][j] 表示 i 到 j 真实的最短路径并上的点的集合。然后只需要用 bitset 优化这个过程即可。
K - xay loves sequence
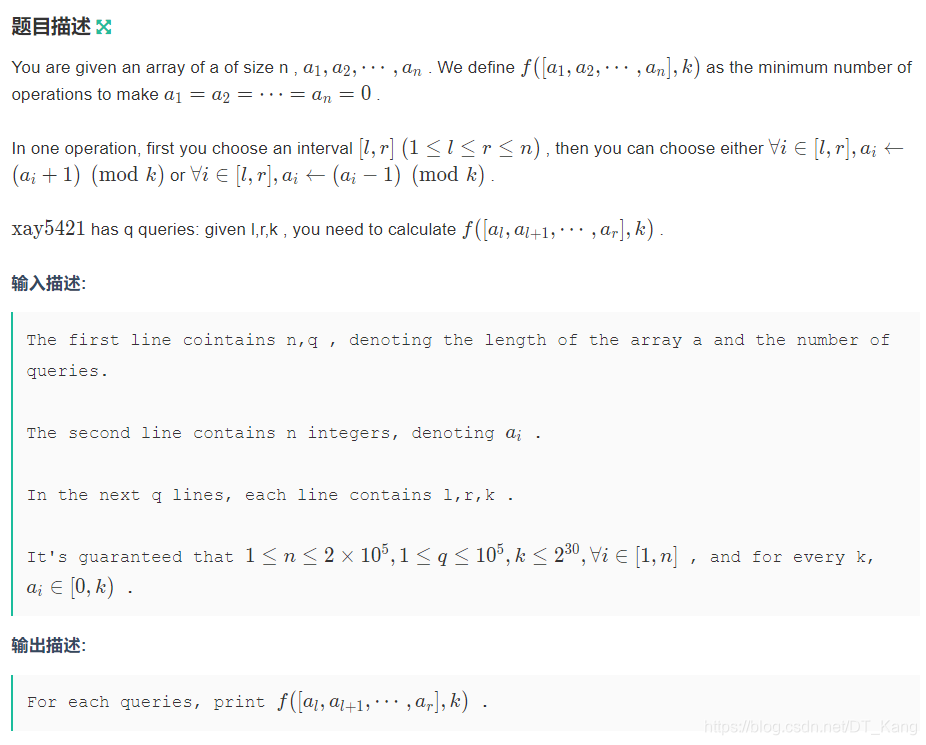
先不考虑 mod K,首先想到差分。但我没想到把 c n + 1 c_{n+1} cn+1 考虑进来。如果不考虑这一项,答案是 max { ∑ c i > 0 ∣ c i ∣ , ∑ c i < 0 ∣ c i ∣ } \max\{\sum_{c_i>0}|c_i|, \sum_{c_i<0}|c_i|\} max{
∑ci>0∣ci∣,∑ci<0∣ci∣};如果考虑这一项,因为 ∑ c i = 0 \sum c_i=0 ∑ci=0,因此答案就是 1 2 ∑ ∣ c i ∣ \frac 1 2\sum |c_i| 21∑∣ci∣,后面算起来简单多了。
现在考虑 mod K,相当于把某些 c 加上 K,相同数量的 c 减去 K。最优情况一定是把若干小于零的 c 往上加,把若干大于零的 c 往下减,这样收益都是 2 ∣ c i ∣ − K 2|c_i|-K 2∣ci∣−K。注意到如果有某个 ci 小于零,一定有另一个 ci 大于零,因此这总是可以成对做到的。因此做法就是把大于零和小于零的 ci 分别按照 2 ∣ c i ∣ − K 2|c_i|-K 2∣ci∣−K 排序,然后取最大的前缀和即可。注意到前缀和是凸的,因此可以二分。std 是在主席树外面二分加一个 log,但完全可以放在主席树里面找到第一个小于零的位置。
contest9
C - Cells

普及一下 LVG引理 。列出来以后可以运用线性代数技巧化简为范德蒙德行列式然后 NTT()
G - Glass Balls

contest10
D - Diameter Counting
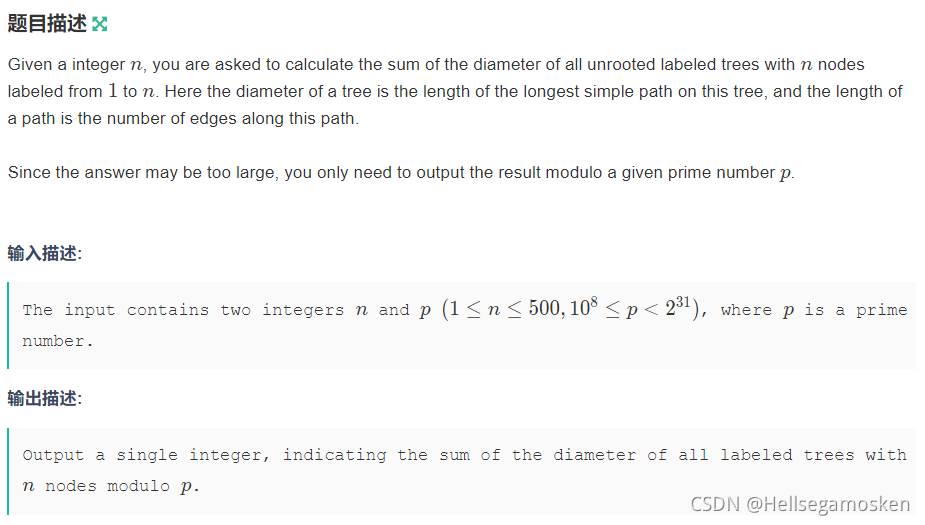
2019 ICPC Asia Xuzhou Regional
L (Loli, Yen-Jen, and a cool problem)
题意:给定一棵树,每个节点有一个字母,多次询问,求从某个结点向上 L 长度的字符串在树中出现了多少次。
这是个广义 SAM 模板题。
至于 SAM 这个东西还是理解为在反串后缀树上跳来跳去比较直观。
要注意的时候建广义 SAM 的时候可以先把 trie 建出来,然后直接在 trie 上建。在线的建法不能只是简单的把 last 记为在原树上的父节点,因为这样 SAM 中可能会产生许多相同的点。正确的做法是先判断当前节点在 SAM 中是否已经存在,具体见 Insert()。
# include <bits/stdc++.h>
# define ll long long
# define ld long double
# define pb push_back
# define fir first
# define sec second
# define rep(i, l, r) for (int i = l; i <= r; i++)
# define per(i, r, l) for (int i = r; i >= l; i--)
using namespace std;
typedef pair <int, int> P;
const int N = 600010;
vector <int> e[N];
char s[N];
int lst, l[N], fa[N], cnt, ch[N][26], f[N][21], a[N], wb[N], size[N], node[N];
int read() {
int x = 0; char c = getchar(), flag = '+';
while (!isdigit(c)) flag = c, c = getchar();
while (isdigit(c)) x = x * 10 + c - '0', c = getchar();
return flag == '-' ? -x : x;
}
int Insert(int c, int p) {
if (ch[p][c]) {
int q = ch[p][c];
if (l[q] == l[p] + 1) return q;
else {
int nq = ++cnt;
memcpy(ch[nq], ch[q], sizeof(ch[q]));
l[nq] = l[p] + 1;
fa[nq] = fa[q], fa[q] = nq;
for (; ch[p][c] == q; p = fa[p]) ch[p][c] = nq;
return nq;
}
} else {
int np = ++cnt;
l[np] = l[p] + 1;
for (; p && !ch[p][c]; p = fa[p]) ch[p][c] = np;
if (!p) fa[np] = 1;
else {
int q = ch[p][c];
if (l[q] == l[p] + 1) fa[np] = q;
else {
int nq = ++cnt;
memcpy(ch[nq], ch[q], sizeof(ch[q]));
l[nq] = l[p] + 1;
fa[nq] = fa[q];
fa[q] = fa[np] = nq;
for (; ch[p][c] == q; p = fa[p]) ch[p][c] = nq;
}
}
return np;
}
}
void dfs(int u, int ff, int lst) {
int temp = node[u] = Insert(s[u] - 'A', lst);
size[temp]++;
rep (i, 1, e[u].size()) {
int v = e[u][i - 1];
if (v == ff) continue;
dfs(v, u, temp);
}
}
int main() {
int n = read(), q = read();
scanf("%s", s + 1);
rep (i, 2, n) {
int x = read();
e[x].pb(i);
}
cnt = 1;
dfs(1, 0, 1);
rep (i, 1, cnt) f[i][0] = fa[i], wb[l[i]]++;
rep (j, 1, 20) rep (i, 1, cnt) f[i][j] = f[f[i][j-1]][j-1];
rep (i, 1, n) wb[i] += wb[i-1];
rep (i, 1, cnt) a[wb[l[i]]--] = i;
per (i, cnt, 1) size[fa[a[i]]] += size[a[i]];
while (q--) {
int x = read(), L = read();
x = node[x];
per (j, 20, 0) if (l[f[x][j]] >= L) x = f[x][j];
cout << size[x] << '\n';
}
return 0;
}
/* by DT_Kang */