Generative Modeling by Estimating Gradients of the Data Distribution阅读笔记

概述

论文提出了一种生成模型，并将其用于图像生成任务。
论文先介绍了传统score-based generative modeling方法，然后分析传统score-based generative modeling存在的问题，最后提出解决问题的算法noise conditional score network。

传统score-based generative modeling介绍

假设数据集中的数据服从$p_{data}(\mathbf{x})$分布。
generative modeling的目标是学习一个生成模型来生成服从$p_{data}(\mathbf{x})$分布的新样本。
定义score function为对概率密度函数$p(\mathbf{x})$求导${\nabla }_{\mathbf{x}}\log p(\mathbf{x})$。
定义score network是一个参数为$\theta$的神经网络$s_{\theta }$，其试图近似score function。
score-based generative modeling通过学习score function，加上Langevin dynamics采样，来生成符合分布的新样本，步骤如下图所示：

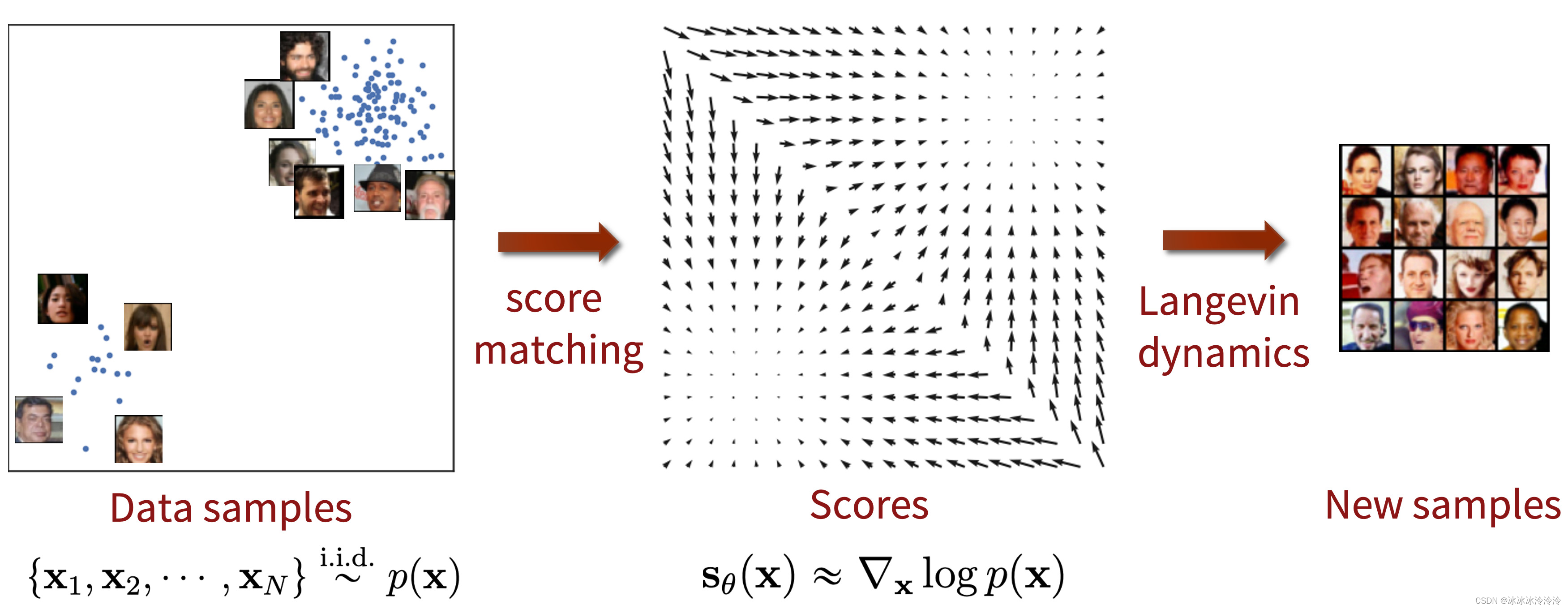
score matching

使用score matching算法，我们可以直接训练一个分数网络$s_{\theta }(\mathbf{x})$来估计${\nabla }_{\mathbf{x}}\log p_{data}(\mathbf{x})$而无需训练模型估计$p_{data}(\mathbf{x})$。好处是可以避免概率密度函数中的归一化常数，详见score matching算法介绍。
score matching算法的优化目标如下：
$$\frac{1}{2}{\mathbb{E}}_{p_{data}}[\Vert {\mathbf{s}}_{\theta }(\mathbf{x})-{\nabla }_{\mathbf{x}}\log p_{data}(\mathbf{x}){\Vert }_2^2]$$上面的公式需要计算${\nabla }_{\mathbf{x}}\log p_{data}(\mathbf{x})$，这是一个非参数估计问题，并不好计算。值得高兴的是，上面的公式在相差常数上等价为$${\mathbb{E}}_{p_{data}}[\text{tr}({\nabla }_{\mathbf{x}}{\mathbf{s}}_{\theta }(\mathbf{x}))+\frac{1}{2}\Vert {\mathbf{s}}_{\theta }(\mathbf{x}){\Vert }_2^2]$$最小化上面的公式可以求出${\mathbf{s}}_{\theta }(\mathbf{x})$。在现实中，期望可以用样本的平均代替。
但是，高维数据计算$\text{tr}({\nabla }_{\mathbf{x}}{\mathbf{s}}_{\theta }(\mathbf{x}))$复杂度很高。Denoising score matching和Sliced score matching是针对高维大数据的两种常用的改进方法。

Langevin dynamics

Langevin dynamics是一种只需要score function${\nabla }_{\mathbf{x}}\log p(\mathbf{x})$就可以从概率密度函数$p_{data}(\mathbf{x})$中采样的方法，它是一种Markov chain Monte Carlo (MCMC)方法。
给一个初始分布${\tilde{\mathbf{x}}}_0\sim \pi (\mathbf{x})$，和固定的步长$ϵ>0$，Langevin方法循环地重复下面的步骤：
$${\tilde{\mathbf{x}}}_t={\tilde{\mathbf{x}}}_{t-1}+\frac{ϵ}{2}{\nabla }_{\mathbf{x}}\log p({\tilde{\mathbf{x}}}_{t-1})+\sqrt{ϵ}{\mathbf{z}}_t$$其中${\mathbf{z}}_t\sim \mathcal{N}(0,\mathbf{I})$。当$ϵ\to 0$，$T\to \infty$时，${\tilde{\mathbf{x}}}_T$的分布是$p_{data}(\mathbf{x})$。

传统score-based generative modeling存在的问题

流形假设上的问题

流形（manifold）假设指出，现实世界中的数据倾向于集中在嵌入高维空间（也称为环境空间）中的低维流形上。

The manifold hypothesis states that data in the real world tend to concentrate on low dimensional manifolds embedded in a high dimensional space (a.k.a., the ambient space).

在流形假设下，score-based generative models存在两个问题：

1. ${\nabla }_{\mathbf{x}}\log p_{data}(\mathbf{x})$在低维流形上没有定义。
2. 只有在数据分布是整个空间时，score估计量才具有一致性(consistent)。

低密度区域的问题

1. 在数据的低密度区域，并没有足够的数据样本去准确地学习score function。
2. 当数据分布的两个峰(mode)被低密度区域分隔时，Langevin dynamics将无法在合理的时间内正确恢复这两个峰的相对权重，并且可能不会收敛到真实分布。例如，假设$p_{data}(\mathbf{x})=\pi p_1(\mathbf{x})+(1-\pi )p_2(\mathbf{x})$，并且$p_1$和$p_2$没有相交的支撑集，在求导后，权重$\pi$将不会影响score function。

Noise Conditional Score Network

为了解决上面的问题，作者对传统score-based generative modeling进行了改进。
作者提出通过 1) 使用各种噪声水平来扰动数据；2）用一个条件分数网络(conditional score network)同时估计所有噪声水平对应的分数。
在条件分数网络训练结束后，使用Langevin dynamics来生成样本时，最开始使用高噪声对应的分数，然后逐渐降低噪音。 这有助于将高噪声的好处平稳地转移到低噪声。而低噪声干扰的数据与原始数据几乎无法区分。

原理如下图，通过加入噪声，可以使数据填充低数据密度区域以提高估计分数的准确性。
较大的噪声显然可以覆盖更多的低密度区域以获得更好的分数估计，但它会过度破坏数据并显着改变原始分布。另一方面，较小的噪声会导致原始数据分布的损坏较少，但不会像我们希望的那样覆盖低密度区域。所以作者提出了使用多尺度的噪声干扰。

噪声条件分数网络(Noise Conditional Score Networks)

{ σ i } i = 1 L \{\sigma_i\}_{i=1}^L { σi​}i=1L​是一系列噪声水平，满足条件$\frac{{\sigma }_1}{{\sigma }_2}=\cdots =\frac{{\sigma }_{L-1}}{{\sigma }_L}>1$，$q_{\sigma }(\mathbf{x})\triangleq \int p_{data}(\mathbf{t})\mathcal{N}(\mathbf{x}|\mathbf{t},{\sigma }^2\mathbf{I})d\mathbf{t}$是噪声扰动后的数据分布。我们要学习一个噪声条件分数网络$s_{\theta }(\mathbf{x},\sigma )$来估计噪声数据的分数，也就是$s_{\theta }(\mathbf{x},\sigma )\approx {\nabla }_{\mathbf{x}}\log q_{\sigma }(\mathbf{x})$。注意这里的分数网络是条件分数网络，输入相较于传统的$s_{\theta }(\mathbf{x})$多了一个$\sigma$。
作者考虑的是图像生成的问题，所以$s_{\theta }(\mathbf{x},\sigma )$的结构作者选择的是U-Net。

对于噪声条件分数网络的训练，作者选择的噪声分布是
$q_{\sigma }(\tilde{\mathbf{x}}|\mathbf{x})=\mathcal{N}(\tilde{\mathbf{x}}|\mathbf{x},{\sigma }^2\mathbf{I})$。
对于一个给定的噪声$\sigma$，优化的目标是：
$$l(\theta ,\sigma )=\frac{1}{2}{\mathbb{E}}_{p_{data}}{\mathbb{E}}_{\tilde{\mathbf{x}}\sim \mathcal{N}(x,{\sigma }^2\mathbf{I})}[\Vert s_{\theta }(\tilde{\mathbf{x}},\sigma )+\frac{\tilde{\mathbf{x}}-\mathbf{x}}{{\sigma }^2}{\Vert }_2^2]$$将所有的噪声融合在一个式子中有：
L ( θ ; { σ i } i = 1 L ) ≜ 1 L ∑ i = 1 L λ ( σ i ) l ( θ , σ i ) \mathcal{L}(\theta;\{\sigma_i\}_{i=1}^L)\triangleq\frac{1}{L}\sum_{i=1}^L\lambda(\sigma_i)\mathcal{l}(\theta,\sigma_i) L(θ;{ σi​}i=1L​)≜L1​i=1∑L​λ(σi​)l(θ,σi​)其中$\lambda ({\sigma }_i)$是权重。

annealed Langevin dynamics

在噪声条件分数网络$s_{\theta }(\mathbf{x};\sigma )$训练完成之后，作者提出annealed Langevin dynamics算法来生成样本， 如算法1所示。先使用高噪声对应的分数，然后逐渐降低噪音。

参考

Yang Song’s blog《Generative Modeling by Estimating Gradients of the Data Distribution》
NIPS 2019《Generative Modeling by Estimating Gradients of the Data Distribution》