汉诺塔问题
在归并排序和构建二叉树中,我们都是将原问题分解为两个规模为原问题一半的子问题。然而对于汉诺塔问题,我们采用不同的分解策略。
!!! question
给定三根柱子,记为 `A`、`B` 和 `C` 。起始状态下,柱子 `A` 上套着 $n$ 个圆盘,它们从上到下按照从小到大的顺序排列。我们的任务是要把这 $n$ 个圆盘移到柱子 `C` 上,并保持它们的原有顺序不变。在移动圆盘的过程中,需要遵守以下规则。
1. 圆盘只能从一个柱子顶部拿出,从另一个柱子顶部放入。
2. 每次只能移动一个圆盘。
3. 小圆盘必须时刻位于大圆盘之上。
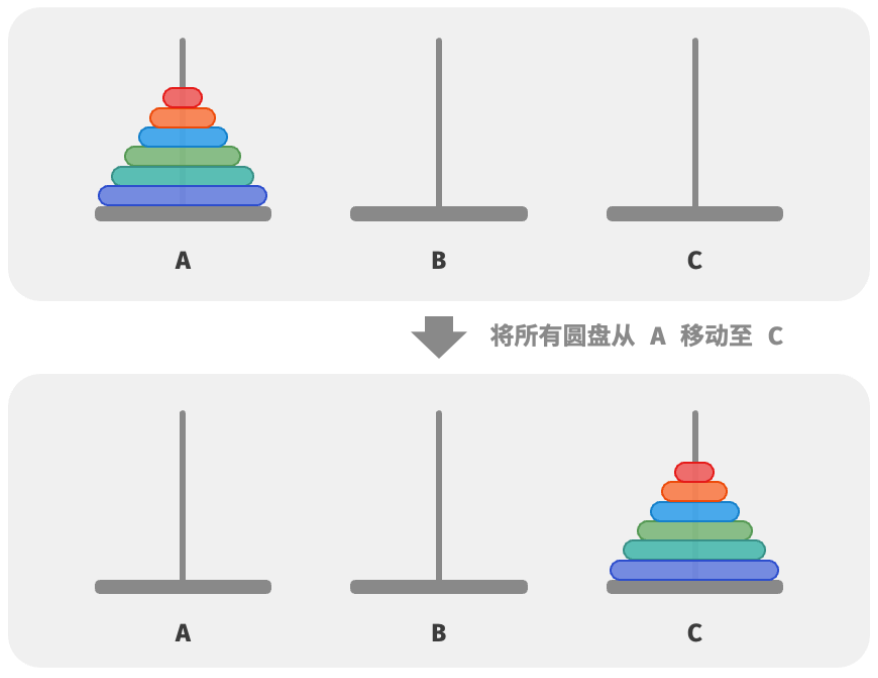
我们将规模为 i i i 的汉诺塔问题记做 f ( i ) f(i) f(i) 。例如 f ( 3 ) f(3) f(3) 代表将 3 3 3 个圆盘从 A 移动至 C 的汉诺塔问题。
考虑基本情况
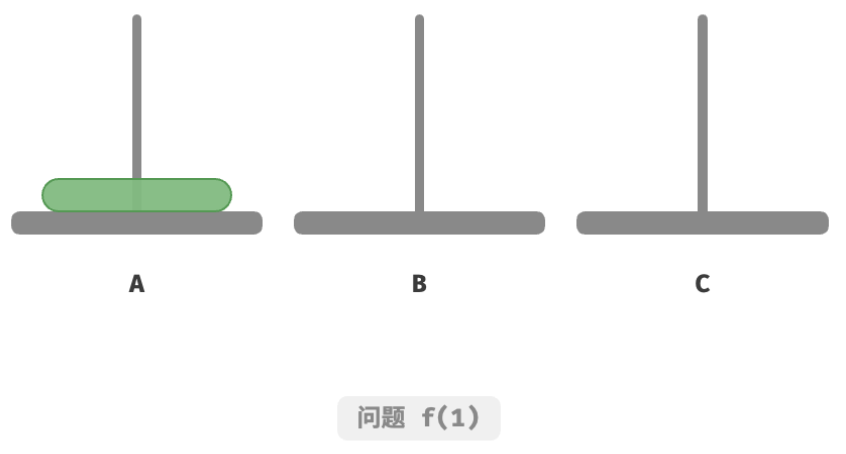
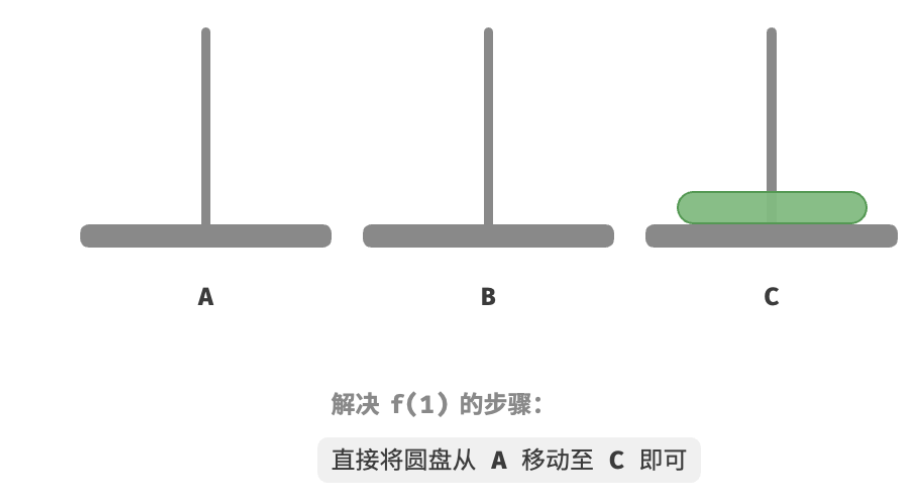
如下图所示,对于问题 f ( 1 ) f(1) f(1) ,即当只有一个圆盘时,我们将它直接从 A 移动至 C 即可。
=== “<1>”
=== “<2>”
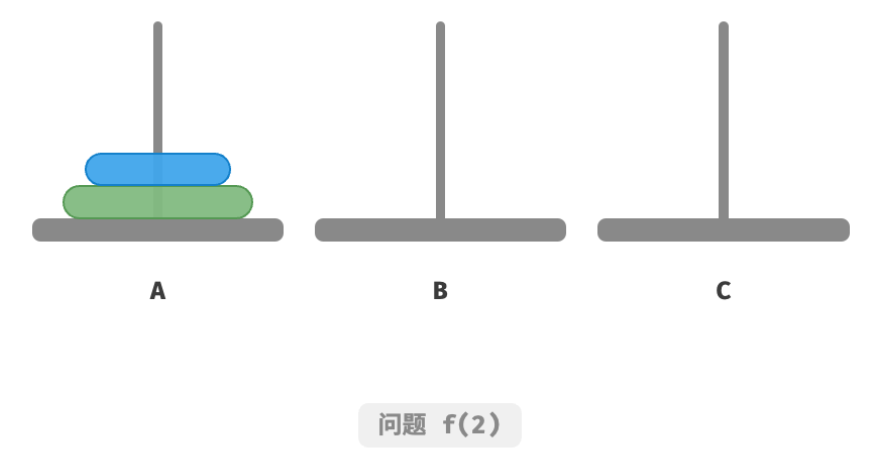
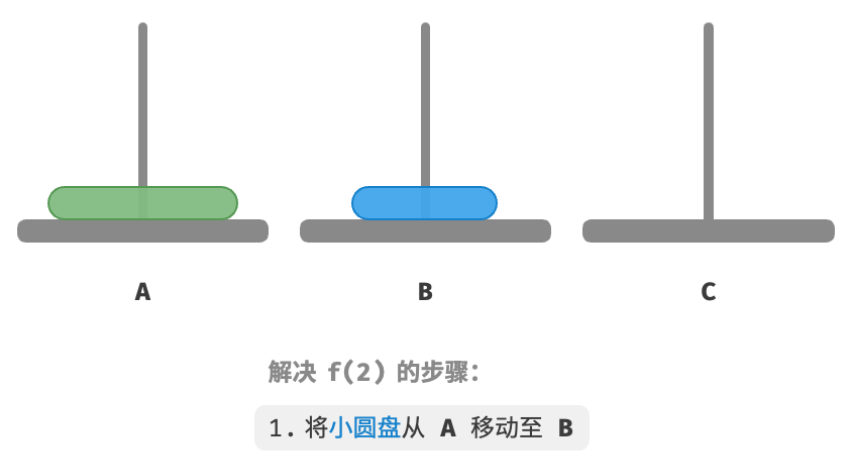
如下图所示,对于问题 f ( 2 ) f(2) f(2) ,即当有两个圆盘时,由于要时刻满足小圆盘在大圆盘之上,因此需要借助 B 来完成移动。
- 先将上面的小圆盘从
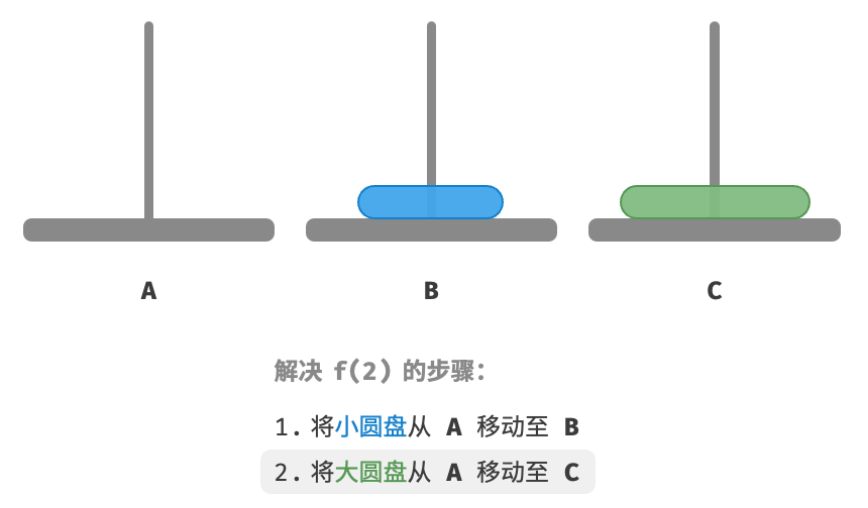
A移至B。 - 再将大圆盘从
A移至C。 - 最后将小圆盘从
B移至C。
=== “<1>”
=== “<2>”
=== “<3>”

=== “<4>”
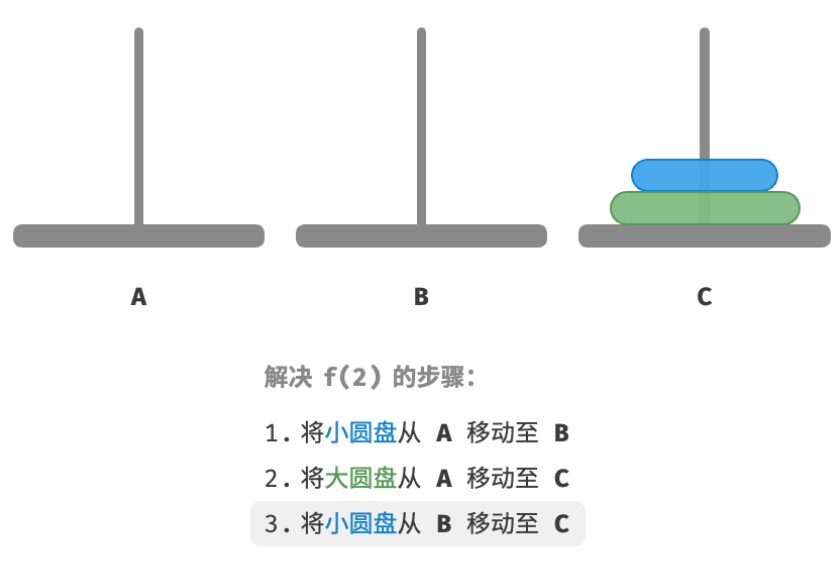
解决问题 f ( 2 ) f(2) f(2) 的过程可总结为:将两个圆盘借助 B 从 A 移至 C 。其中,C 称为目标柱、B 称为缓冲柱。
子问题分解
对于问题 f ( 3 ) f(3) f(3) ,即当有三个圆盘时,情况变得稍微复杂了一些。
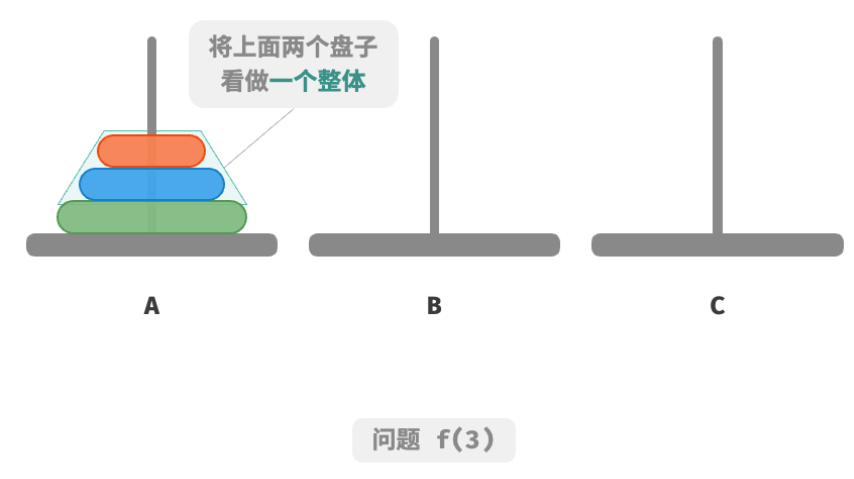
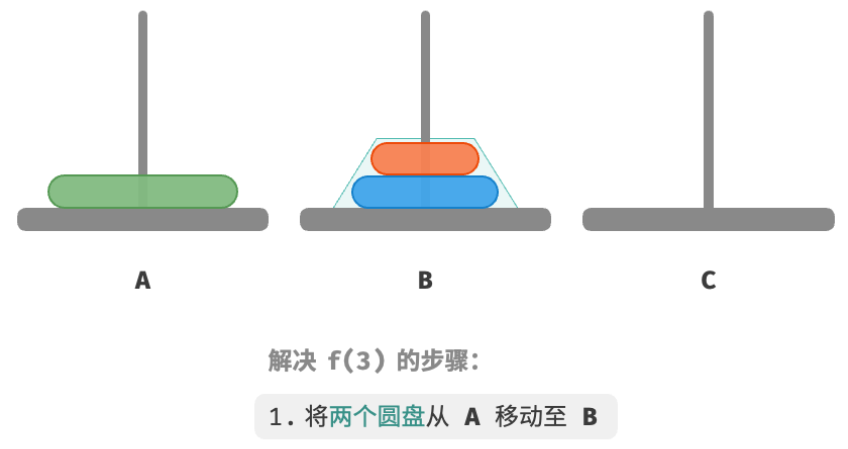
因为已知 f ( 1 ) f(1) f(1) 和 f ( 2 ) f(2) f(2) 的解,所以我们可从分治角度思考,将 A 顶部的两个圆盘看做一个整体,执行下图所示的步骤。这样三个圆盘就被顺利地从 A 移动至 C 了。
- 令
B为目标柱、C为缓冲柱,将两个圆盘从A移动至B。 - 将
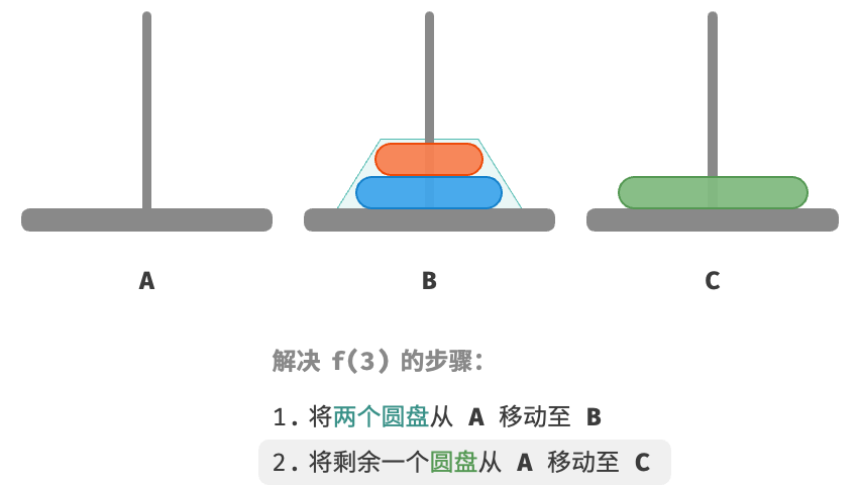
A中剩余的一个圆盘从A直接移动至C。 - 令
C为目标柱、A为缓冲柱,将两个圆盘从B移动至C。
=== “<1>”
=== “<2>”
=== “<3>”
=== “<4>”
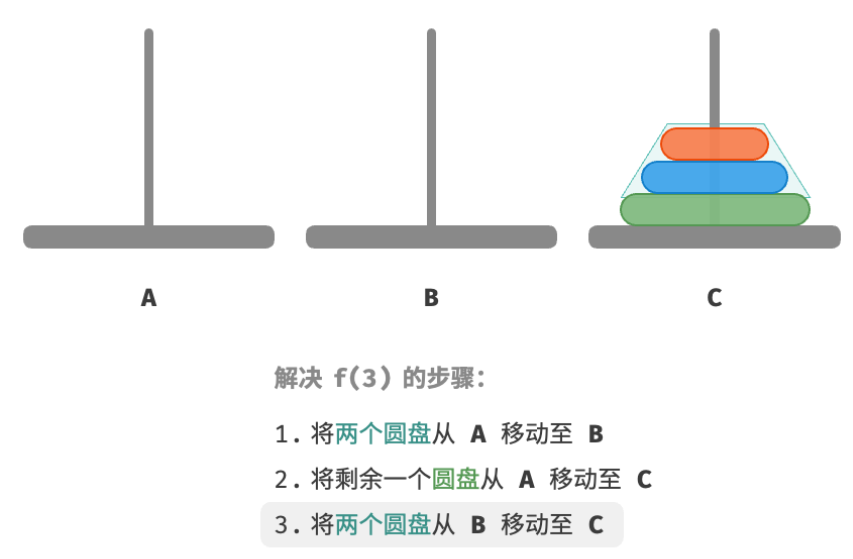
本质上看,我们将问题 f ( 3 ) f(3) f(3) 划分为两个子问题 f ( 2 ) f(2) f(2) 和子问题 f ( 1 ) f(1) f(1) 。按顺序解决这三个子问题之后,原问题随之得到解决。这说明子问题是独立的,而且解是可以合并的。
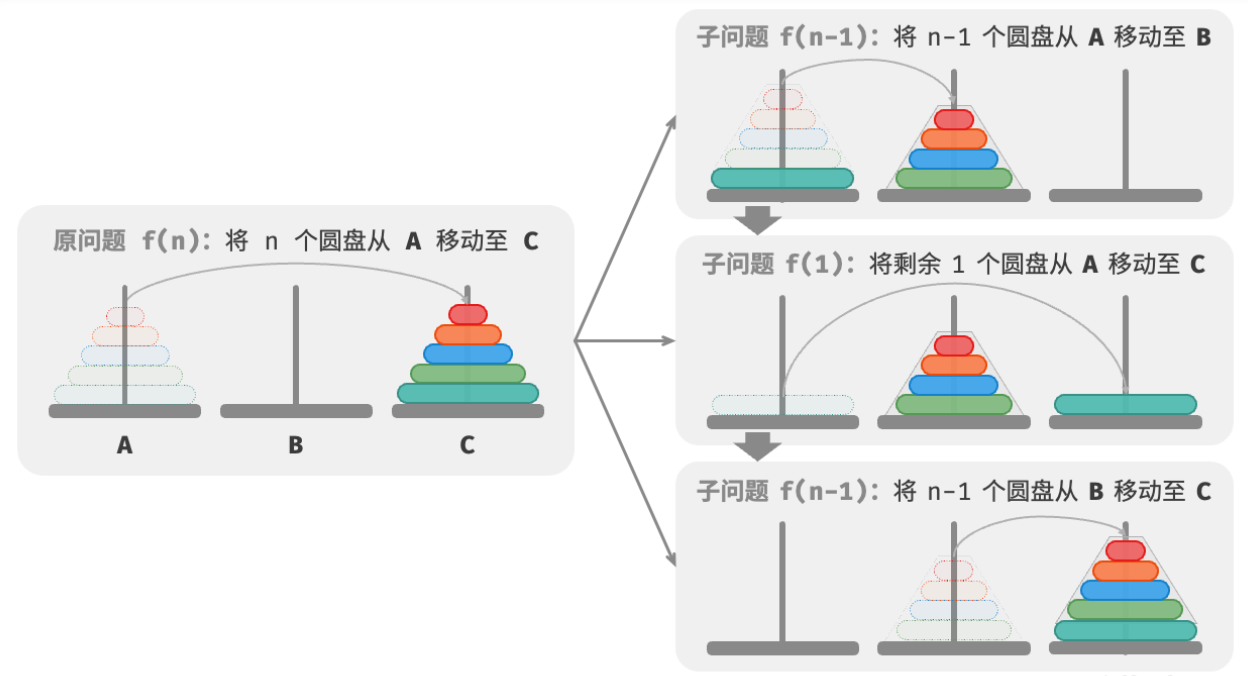
至此,我们可总结出下图所示的汉诺塔问题的分治策略:将原问题 f ( n ) f(n) f(n) 划分为两个子问题 f ( n − 1 ) f(n-1) f(n−1) 和一个子问题 f ( 1 ) f(1) f(1) ,并按照以下顺序解决这三个子问题。
- 将 n − 1 n-1 n−1 个圆盘借助
C从A移至B。 - 将剩余 1 1 1 个圆盘从
A直接移至C。 - 将 n − 1 n-1 n−1 个圆盘借助
A从B移至C。
对于这两个子问题 f ( n − 1 ) f(n-1) f(n−1) ,可以通过相同的方式进行递归划分,直至达到最小子问题 f ( 1 ) f(1) f(1) 。而 f ( 1 ) f(1) f(1) 的解是已知的,只需一次移动操作即可。
代码实现
在代码中,我们声明一个递归函数 dfs(i, src, buf, tar) ,它的作用是将柱 src 顶部的 i i i 个圆盘借助缓冲柱 buf 移动至目标柱 tar 。
=== “Python”
```python title="hanota.py"
[class]{}-[func]{move}
[class]{}-[func]{dfs}
[class]{}-[func]{solve_hanota}
```
=== “C++”
```cpp title="hanota.cpp"
[class]{}-[func]{move}
[class]{}-[func]{dfs}
[class]{}-[func]{solveHanota}
```
=== “Java”
```java title="hanota.java"
[class]{hanota}-[func]{move}
[class]{hanota}-[func]{dfs}
[class]{hanota}-[func]{solveHanota}
```
=== “C#”
```csharp title="hanota.cs"
[class]{hanota}-[func]{move}
[class]{hanota}-[func]{dfs}
[class]{hanota}-[func]{solveHanota}
```
=== “Go”
```go title="hanota.go"
[class]{}-[func]{move}
[class]{}-[func]{dfsHanota}
[class]{}-[func]{solveHanota}
```
=== “Swift”
```swift title="hanota.swift"
[class]{}-[func]{move}
[class]{}-[func]{dfs}
[class]{}-[func]{solveHanota}
```
=== “JS”
```javascript title="hanota.js"
[class]{}-[func]{move}
[class]{}-[func]{dfs}
[class]{}-[func]{solveHanota}
```
=== “TS”
```typescript title="hanota.ts"
[class]{}-[func]{move}
[class]{}-[func]{dfs}
[class]{}-[func]{solveHanota}
```
=== “Dart”
```dart title="hanota.dart"
[class]{}-[func]{move}
[class]{}-[func]{dfs}
[class]{}-[func]{solveHanota}
```
=== “Rust”
```rust title="hanota.rs"
[class]{}-[func]{move_pan}
[class]{}-[func]{dfs}
[class]{}-[func]{solve_hanota}
```
=== “C”
```c title="hanota.c"
[class]{}-[func]{move}
[class]{}-[func]{dfs}
[class]{}-[func]{solveHanota}
```
=== “Zig”
```zig title="hanota.zig"
[class]{}-[func]{move}
[class]{}-[func]{dfs}
[class]{}-[func]{solveHanota}
```
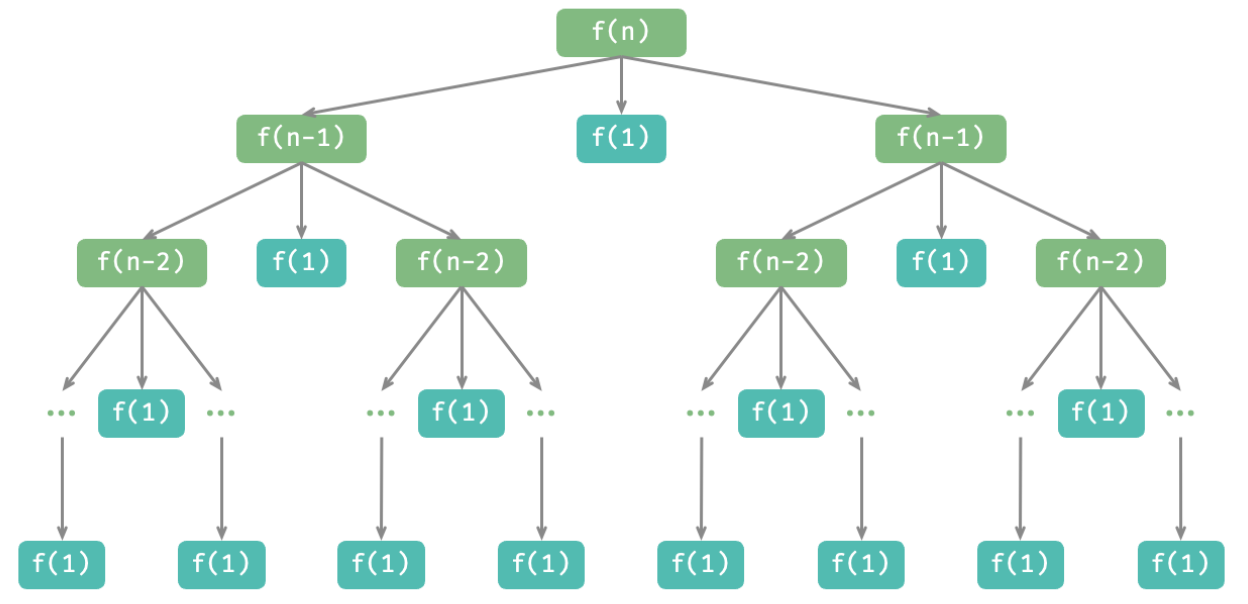
如下图所示,汉诺塔问题形成一个高度为 n n n 的递归树,每个节点代表一个子问题、对应一个开启的 dfs() 函数,因此时间复杂度为 O ( 2 n ) O(2^n) O(2n) ,空间复杂度为 O ( n ) O(n) O(n) 。
!!! quote
汉诺塔问题源自一种古老的传说故事。在古印度的一个寺庙里,僧侣们有三根高大的钻石柱子,以及 $64$ 个大小不一的金圆盘。僧侣们不断地移动原盘,他们相信在最后一个圆盘被正确放置的那一刻,这个世界就会结束。
然而,即使僧侣们每秒钟移动一次,总共需要大约 $2^{64} \approx 1.84×10^{19}$ 秒,合约 $5850$ 亿年,远远超过了现在对宇宙年龄的估计。所以,倘若这个传说是真的,我们应该不需要担心世界末日的到来。