仍然是西蒙.赫金的《自适应滤波器原理》第四版,距离上次看这本书已经过去半个月,要抓点紧了。本文主要包括:
1)何为维纳滤波器(Wiener Filter);
2)Wiener滤波器的推导;
3)应用实例;
4)Wiener变体;
内容为自己的学习总结,内容多有参考他人,最后一并给出链接。
一、维纳滤波器简介
A-基本概念
对于滤波器的具体实现,都依赖两个选择:
1)Filter的impulse选择(FIR / IIR)
2)统计优化准则的选择
维纳滤波器:由数学家维纳(Rorbert Wiener)提出的一种以最小平方(统计准则)为最优准则的线性滤波器。何为线性滤波器?文中图:

B-几个问题
在具体讨论之前,先来说说自己看的时候,想到的几个问题:
问题1:维纳滤波器与自适应滤波是什么关系,与LMS呢?
个人观点:常用的hamming、taylor都是固定的滤波器,滤波器参数需要根据信号进行计算调整的,这一类滤波器都是自适应滤波器,跟自己有关嘛,自适应理所当然,维纳滤波器是利用统计参数,实际应用中可能无法得到,需要借助迭代实现,这样就成了一个新框架→自适应滤波器。参数估计呢可以利用梯度下降法迭代逼近,例如常说的LMS就是迭代逼近的一种方式,LMS本身不同于weiner-filter,但迭代结果可以作为wiener-filter的近似。
问题2:维纳滤波器是有限长(FIR-Finite Impulse Response)还是无限长滤波器(IIR-Infinite Impulse Response)?
个人观点:维纳滤波器是大的理论框架,而FIR/IIR只是实现理论的不同途径,故二者均可,下文会一一介绍。
问题3:基于维纳滤波器这个理论框架的应用有哪些?
个人观点:1)自适应是一种解决工程问题的途径,故很多自适应滤波本质都是维纳滤波(不是全部);2)MVDR谱估计(Minimum variance distortionless response)、广义旁瓣相消GSC(Generalized Sidelobe Canceller )等都是维纳框架下的应用。
问题4:卡尔曼滤波(Kalman)是维纳滤波的一种吗?
个人观点:应该不是,维纳滤波器是线性滤波器,而卡尔曼滤波器据说是非线性,具体区别等看到卡尔曼再回头总结。
二、维纳滤波器理论分析
A-有限长维纳滤波(FIR)
1-基本定义
下图是使用M抽头FIR滤波器的结构图:
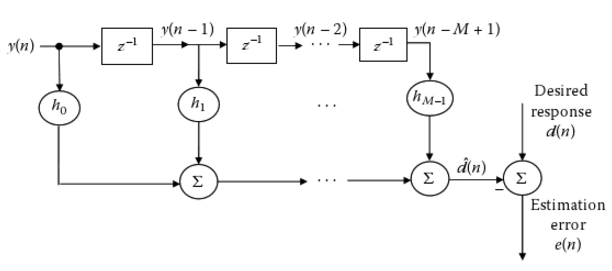
输出为:
d^(n)=∑k=0M−1hky(n−k)d^(n)=∑k=0M−1hky(n−k)
其中hkhk为FIR滤波器系数,M为系数个数。
以下推导基于宽平稳假设,首先计算估计误差:
e(n)=d(n)−d^(n)=d(n)−hTye(n)=d(n)−d^(n)=d(n)−hTy
其中hT=[h0,h1,h2,...,hM−1]hT=[h0,h1,h2,...,hM−1],yT=[y(n),y(n−1),y(n−2),...,y(n−M+1)]yT=[y(n),y(n−1),y(n−2),...,y(n−M+1)]是包括过去M个样本的输入向量。
Wiener Filter基于最小均方误差准则,给出均方误差定义:
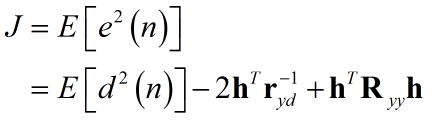
其中,r−1yd=E[yd(n)]ryd−1=E[yd(n)]为输入信号与期望信号的互相关。
2-维纳滤波器求解
最小化估计误差,对其中某个抽头系数求偏导:
∂J∂hk=0⇒−2E[e(n)y(n−k)]=0∂J∂hk=0⇒−2E[e(n)y(n−k)]=0
这就是正交定理(Orthogonality Principle):估计误差e(n)e(n)需要正交与输入信号y(n)y(n)。这也容易理解,在输入信号y(n)y(n)张成的子空间中,更加高维的信息无法被表达,故成了误差。如(x1,y1,z1)(x1,y1,z1)用x、yx、y两个单位向量表达,最小均方误差时z1z1就成了估计误差。
不失一般性,将偏导写成向量/矩阵形式:
∂J∂h=0⇒−2r−1yd+2hTRyy=0∂J∂h=0⇒−2ryd−1+2hTRyy=0
上式hTRyy=r−1ydhTRyy=ryd−1就是Wiener Hopf方程。
得到Wiener Filter最优解hopthopt:
hopt=R−1yyr−1ydhopt=Ryy−1ryd−1
上式就是Wiener-Hopf的解,也就是对应Wiener Filter的解。求解需要矩阵求逆,又相关矩阵为对称且为Toeplitz形式,故可借助数学手段对R高效求逆——Levinson-Durbin算法。
因为在时域分析,此时FIR的解也叫时域维纳滤波器。
B-无限长维纳滤波(IIR)
1-基本定义
滤波器为无限长时,d^(n)=∑k=0M−1hky(n−k)d^(n)=∑k=0M−1hky(n−k)改写为:
d^(n)=∑k=−∞∞hky(n−k)=h(n)∗y(n)d^(n)=∑k=−∞∞hky(n−k)=h(n)∗y(n)
∗∗表示卷积。易证:时域有限长对应频域无限长,时域无限长对应频域有限长,因此对于IIR情形,更希望在频域进行分析。
2-维纳滤波器求解
计算均方误差:
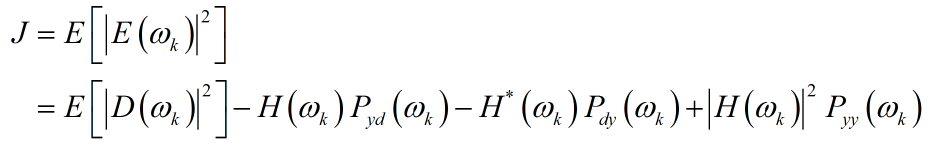
其中E(ωk)E(ωk)为e(n)e(n)的频域变换,Pyd(ωk)=E[Y(ωk)D∗(ωk)]Pyd(ωk)=E[Y(ωk)D∗(ωk)], Pyy(ωk)=E[|Y(ωk)|2]Pyy(ωk)=E[|Y(ωk)|2]。
针对J求解复导数:
∂J∂H(ωk)=0⇒H∗(ωk)Pyy(ωk)−Pyd(ωk)=0∂J∂H(ωk)=0⇒H∗(ωk)Pyy(ωk)−Pyd(ωk)=0
得到频域维纳滤波最优解:
Hopt(ωk)=Pdy(ωk)Pyy(ωk)Hopt(ωk)=Pdy(ωk)Pyy(ωk)
因为在频域分析,此时IIR的解也叫频域维纳滤波器。
三、应用实例
已知:
含有噪声的正弦波:y(n)=s(n)+w(n)=sin(2πfn+θ)+w(n)y(n)=s(n)+w(n)=sin(2πfn+θ)+w(n).
其中f=0.2f=0.2为归一化频率[-1/2, 1/2],θθ为正弦波相位,服从[0,2ππ]的均匀分布,w(n)w(n)为具有零均值和方差σ2=2σ2=2的高斯白噪声。
求:
时域以及频域维纳滤波器。假设滤波器为时域滤波器时M=2M=2.
A-对于时域维纳滤波器:
首先求解相关矩阵:
x(n)x(n)为广义平稳随机过程,可以计算其自相关函数:
rxx(m)=cos(2πfn)rxx(m)=cos(2πfn)
利用上面推导的Wiener-Hopf最优解公式:
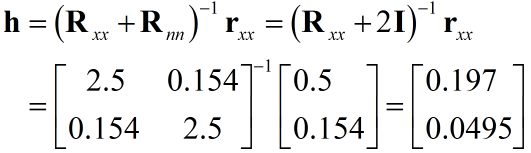
当然也可以求解准则函数JJ,求极值点:

B-对于频域维纳滤波器:
白噪声与信号不相关,直接调用上文推导的公式:
H(ωk)=Pxy(ωk)Pyy(ωk)=Pxx(ωk)Pxx(ωk)+Pnn(ωk)=Pxx(ωk)Pxx(ωk)+2H(ωk)=Pxy(ωk)Pyy(ωk)=Pxx(ωk)Pxx(ωk)+Pnn(ωk)=Pxx(ωk)Pxx(ωk)+2
时域相关函数与频域功率谱互为傅里叶变换,而时域相关函数在求时域维纳滤波时已写出,得出功率谱公式:

当L−>∞L−>∞,将PxxPxx代入上式,即使频域维纳滤波器的解。
C-闲话时域、频域维纳滤波器
时域求解维纳滤波器,但时域对应的都有频域的变换结果,如L=2L=2的频域解就是时域维纳解的傅里叶变换。画出LL不同取值对应的频域幅度响应:
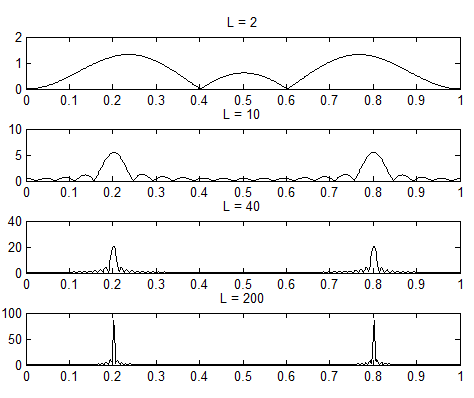
可以观察到:LL趋近∞时,频域响应接近σ(.)σ(.)冲激响应,这与理论:相关函数为时域余弦对应频域冲激响应是一致的。
这个例子只是理想情况,理一理求解的思路,事实上认为信号的自相关为已知,这是不符合实际的。实际应用中如何近似求解呢?给出一个简单例子。
D-基于频域维纳滤波的语音增强
还是利用上面的模型:
y(n)=x(n)+w(n)y(n)=x(n)+w(n)
这里y(n)y(n)是麦克风接收的带噪语音,x(n)x(n)是干净语音信号,w(n)w(n)为白噪声。显然相关函数我们无法得知。
利用一种近似的处理思路:利用前面几个分帧不带语音,估计噪声,从而得到噪声的功率谱近似,利用带噪语音功率减去噪声功率,得到
H(ωk)=Pxy(ωk)Pyy(ωk)=Pxx(ωk)Pxx(ωk)+Pnn(ωk)=Pyy(ωk)−Pnn(ωk)Pyy(ωk)H(ωk)=Pxy(ωk)Pyy(ωk)=Pxx(ωk)Pxx(ωk)+Pnn(ωk)=Pyy(ωk)−Pnn(ωk)Pyy(ωk)
利用估计出的维纳滤波器,即可实现信号的频域滤波。这里只是想到的一个实际例子,至于参数估计、迭代方式则是百花齐放了。
附上主要代码:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
nw = 512; ni = 64;
NIS = 100;
Y =
fft
(enframe(y,hamming(nw),ni)');
Yab =
abs
(Y);
Nest =
mean
(Yab(:,1:NIS),2);
Yest =
zeros
(
size
(Y));
for
i
= 1:
size
(Y,2)
Yest(:,
i
) = Yab(:,
i
).*((Yab(:,
i
)-Nest)./Yab(:,
i
));
end
Ye = Yest.*
exp
(1j*
angle
(Y));
result =
zeros
(1,
length
(y));
%estimation
for
i
=1:
size
(Y,2);
pos = ((
i
-1)*ni+1):((
i
-1)*ni+nw);
result(pos) = result(pos)+
real
(
ifft
(Ye(:,
i
))).';
end
result = result/
max
(
abs
(result));
|
上面思路处理结果:
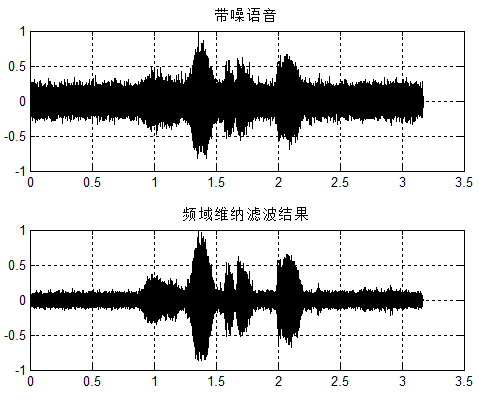
可以看出维纳降噪多少还是有些效果的,H(ωk)=Pxy(ωk)Pyy(ωk)=Pxx(ωk)Pxx(ωk)+Pnn(ωk)=11+1/SNRH(ωk)=Pxy(ωk)Pyy(ωk)=Pxx(ωk)Pxx(ωk)+Pnn(ωk)=11+1/SNR可以看出SNR越小,维纳滤波器衰减越大。
四、Wiener Filter变体
A-平方根维纳滤波
使用维纳滤波器的平方根,则滤波器在频域的滤波结果为:
X^(ωk)=H(ωk)−−−−−−√Y(ωk)X^(ωk)=H(ωk)Y(ωk)
仍然基于噪声与信号不相关的假设,分析滤波后信号的功率谱:
E∣∣X^(ωk)∣∣2=Px^x^=H(ωk)E|Y(ωk)|2=H(ωk)Pyy(ωk)=Pxx(ωk)E|X^(ωk)|2=Px^x^=H(ωk)E|Y(ωk)|2=H(ωk)Pyy(ωk)=Pxx(ωk)
可见采用平方根维纳滤波,滤波器输出信号的功率谱与纯净信号的功率谱相等。
B-参变维纳滤波器
以频域Wiener Filter为例:
H(ωk)=Pxy(ωk)Pyy(ωk)=Pxx(ωk)Pxx(ωk)+Pnn(ωk)H(ωk)=Pxy(ωk)Pyy(ωk)=Pxx(ωk)Pxx(ωk)+Pnn(ωk)
很自然地,可以将其扩展为广义Wiener Filter形式:
H(ωk)=(Pxx(ωk)Pxx(ωk)+αPnn(ωk))βH(ωk)=(Pxx(ωk)Pxx(ωk)+αPnn(ωk))β
这样通过调节(αα,ββ )即可对滤波器进行微调。
参考:
Philipos C.Loizou《speech enhancement theory and practice》.
Simon Haykin 《Adaptive Filter Theory Fourth Edition》.