如果我们指定了一个方向,则在各个方向上的接收天线,能收到的能量满足:
∣ G ( ψ ) ∣ = { ∣ s i n ( N ψ / 2 ) N s i n ( ψ / 2 ) ∣ , if ψ ≠ 0 1 , if ψ = 0 − − − − − − 公式 ( 1 ) |G(\psi)|= \begin{cases} |\frac{sin(N\psi/2)}{Nsin(\psi/2)}|, & \text {if $\psi \neq 0$} \\ 1, & \text{if $\psi=0$} \end{cases} ------公式(1) ∣G(ψ)∣={
∣Nsin(ψ/2)sin(Nψ/2)∣,1,if ψ=0if ψ=0−−−−−−公式(1)
其中:
ψ = 2 π d λ c o s ( θ ) − 2 π d λ c o s ( θ 0 ) \psi=\frac{2\pi d}{\lambda}cos(\theta)-\frac{2\pi d}{\lambda}cos(\theta_{0}) ψ=λ2πdcos(θ)−λ2πdcos(θ0)
θ 0 \theta_{0} θ0 表示我们想指向的方向, θ \theta θ 是一个变的量,遍历整个 − π -\pi −π 到 π \pi π 的这样的一圈。为了简单起见,我们不妨设 θ 0 = π / 2 \theta_{0}=\pi/2 θ0=π/2,则:
ψ = 2 π d λ c o s ( θ ) − 2 π d λ c o s ( θ 0 ) = 2 π d λ c o s ( θ ) − 公式 ( 2 ) \psi=\frac{2\pi d}{\lambda}cos(\theta)-\frac{2\pi d}{\lambda}cos(\theta_{0})=\frac{2\pi d}{\lambda}cos(\theta)-公式(2) ψ=λ2πdcos(θ)−λ2πdcos(θ0)=λ2πdcos(θ)−公式(2)
为了只有一个指定的波束方向(指哪儿打哪儿,这里应该理解为数学上的极大值点,应该保证只有一个波束极大值点),则 ψ / 2 \psi /2 ψ/2 应该介于 [ − π / 2 , π / 2 ] [-\pi/2,\pi/2] [−π/2,π/2] 之间,即 2 π d λ c o s ( θ ) \frac{2\pi d}{\lambda}cos(\theta) λ2πdcos(θ) 在 [ − π , π ] [-\pi,\pi] [−π,π] 之间,所以
d λ ≤ 1 2 \frac{d}{\lambda}\leq \frac{1}{2} λd≤21
我们可以画图来感受下,如果
d λ = 1 > 1 2 \frac{d}{\lambda}=1> \frac{1}{2} λd=1>21
那么 ψ = 2 π d λ c o s ( θ ) ∈ [ − 2 π , 2 π ] \psi=\frac{2\pi d}{\lambda}cos(\theta)\in[-2\pi,2\pi] ψ=λ2πdcos(θ)∈[−2π,2π]
则,我们对公式(1),按照上式画出幅度:
import numpy as np
from matplotlib import pyplot as plt
N = 32 #天线数量
psi = np.arange(-2*np.pi, 2*np.pi-0.0000001, 0.01)
r = np.abs(np.sin(N * psi/2)/np.sin(psi/2))/N
plt.figure()
plt.plot(psi/np.pi, r)
plt.grid()
plt.show()

在 [ − π , π ] [-\pi,\pi] [−π,π] 之间只有一个最高点,在这之外,极大值点开始逐渐增大,即在另外一些方向上,也有较大的能量辐射到那个方向上。
所以,当 d λ \frac{d}{\lambda} λd 从 0.5 逐渐增大到 1 的过程中,可以看到多出来的指向逐渐显现出来:
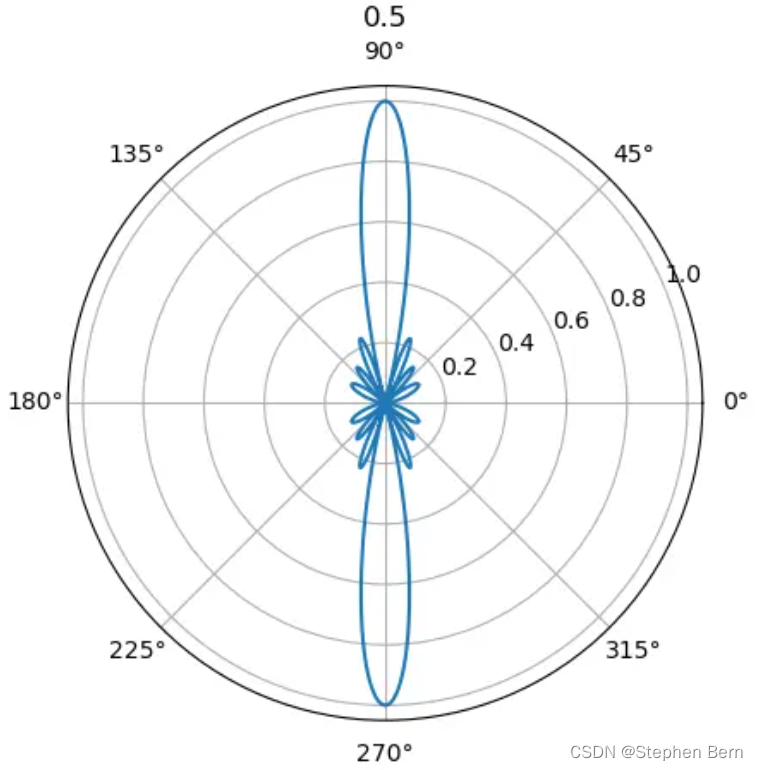
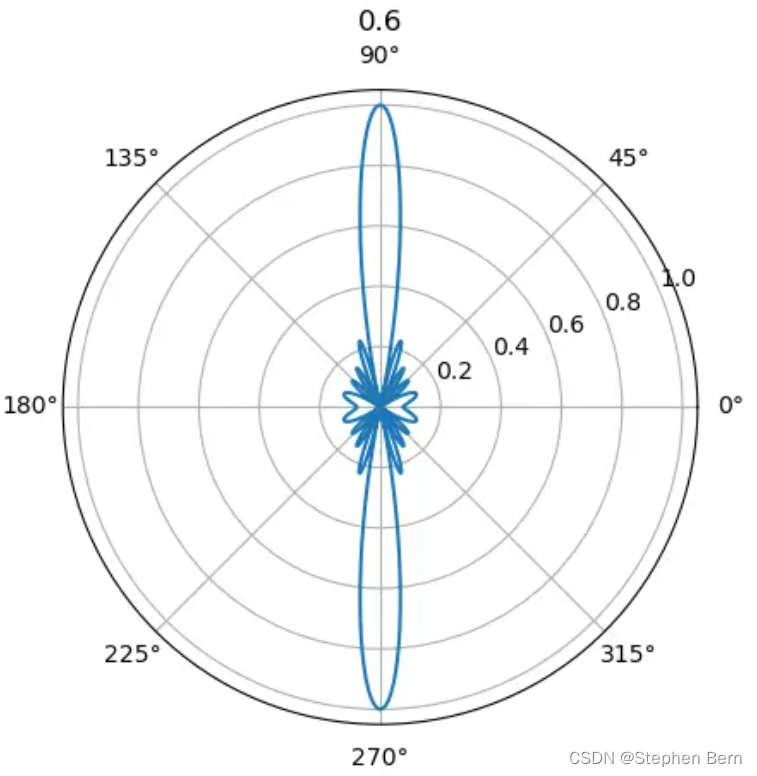

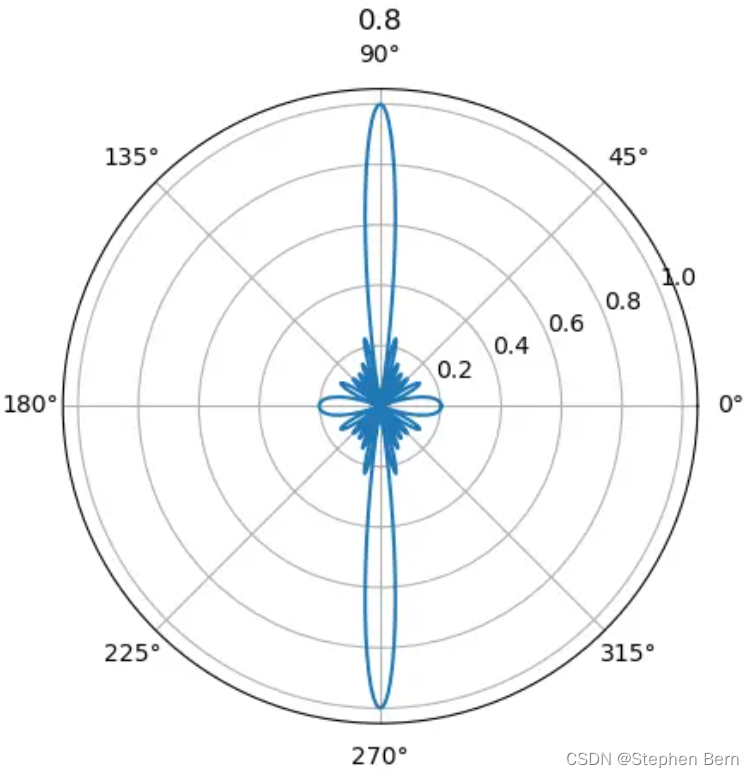
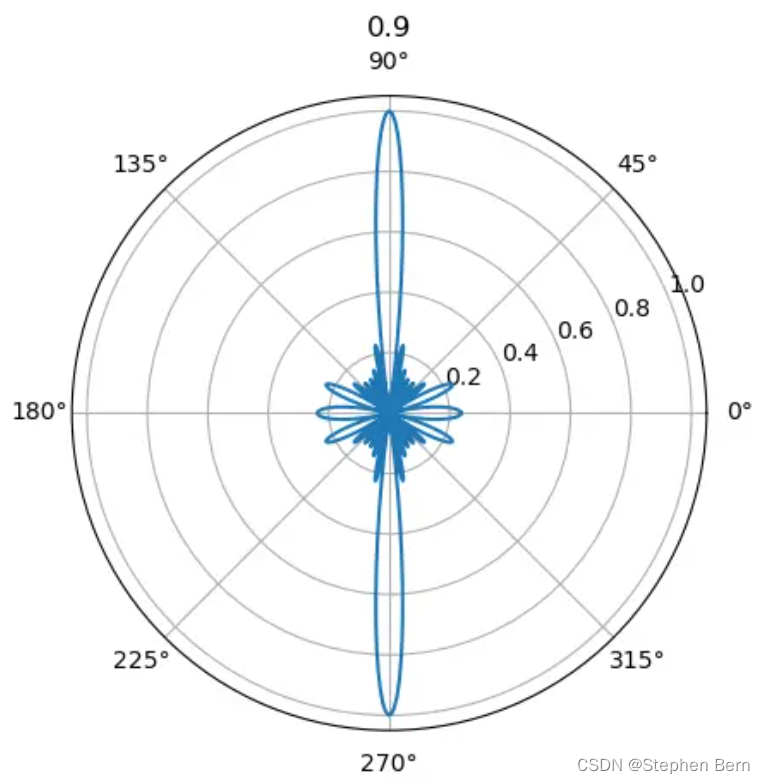

import numpy as np
from matplotlib import pyplot as plt
N = 8 #天线数量
theta = np.arange(0.000001,2*np.pi-0.0000001,0.01)
d_vs_lambda = 0.5
psi = 2 * np.pi * d_vs_lambda * np.cos(theta)
r = np.abs(np.sin(N * psi/2)/np.sin(psi/2))/N
plt.figure()
plt.polar(theta,r)
plt.title("0.5")
plt.show()
d_vs_lambda = 0.6
psi = 2 * np.pi * d_vs_lambda * np.cos(theta)
r = np.abs(np.sin(N * psi/2)/np.sin(psi/2))/N
plt.figure()
plt.polar(theta,r)
plt.title("0.6")
plt.show()
d_vs_lambda = 0.7
psi = 2 * np.pi * d_vs_lambda * np.cos(theta)
r = np.abs(np.sin(N * psi/2)/np.sin(psi/2))/N
plt.figure()
plt.polar(theta,r)
plt.title("0.7")
plt.show()
d_vs_lambda = 0.8
psi = 2 * np.pi * d_vs_lambda * np.cos(theta)
r = np.abs(np.sin(N * psi/2)/np.sin(psi/2))/N
plt.figure()
plt.polar(theta,r)
plt.title("0.8")
plt.show()
d_vs_lambda = 0.9
psi = 2 * np.pi * d_vs_lambda * np.cos(theta)
r = np.abs(np.sin(N * psi/2)/np.sin(psi/2))/N
plt.figure()
plt.polar(theta,r)
plt.title("0.9")
plt.show()
d_vs_lambda = 1.0
psi = 2 * np.pi * d_vs_lambda * np.cos(theta)
r = np.abs(np.sin(N * psi/2)/np.sin(psi/2))/N
plt.figure()
plt.polar(theta,r)
plt.title("1.0")
plt.show()