过拟合与欠拟合原因及解决办法、正则化类别、维灾难、正则化线性模型、岭回归、Lasso 回归、Elastic Net (弹性网络)、岭回归函数及案例使用、sklearn模型的保存和加载

一、过拟合与欠拟合

过拟合：一个假设在训练数据上能够获得比其他假设更好的拟合，但是在测试数据集上却不能很好地拟合数据，此时认为这个假设出现了过拟合的现象(模型过于复杂)
欠拟合：一个假设在训练数据上不能获得更好的拟合，并且在测试数据集上也不能很好地拟合数据，此时认为这个假设出现了欠拟合的现象(模型过于简单)

导致模型复杂的原因：线性回归进行训练学习的时候模型会变得复杂，这里就对应前面再说的线性回归的两种关系，非线性关系的数据，也就是存在很多无用的特征或者现实中的事物特征跟目标值的关系并不是简单的线性关系

1.1 欠拟合原因以及解决办法

原因：学习到数据的特征过少
解决办法
1. 添加其他特征项，有时候我们模型出现欠拟合的时候是因为特征项不够导致的，可以添加其他特征项来很好地解决。例如，“组合”、“泛化”、“相关性”三类特征是特征添加的重要手段，无论在什么场景，都可以照葫芦画瓢，总会得到意想不到的效果。除上面的特征之外，“上下文特征”、“平台特征”等等，都可以作为特征添加的首选项
2. 添加多项式特征，这个在机器学习算法里面用的很普遍，例如将线性模型通过添加二次项或者三次项使模型泛化能力更强。

1.2 过拟合原因以及解决办法

原因：原始特征过多，存在一些嘈杂特征，模型过于复杂是因为模型尝试去兼顾各个测试数据点
解决办法
1. 重新清洗数据，导致过拟合的一个原因也有可能是数据不纯导致的，如果出现了过拟合就需要我们重新清洗数据
2. 增大数据的训练量，还有一个原因就是我们用于训练的数据量太小导致的，训练数据占总数据的比例过小
3. 正则化
4. 减少特征维度，防止维灾难

二、正则化

在解决回归过拟合中，选择正则化
对于其他机器学习算法如分类算法来说也会出现这样的问题，除了一些算法本身作用之外（决策树、神经网络），我们更多的也是去自己做特征选择，包括删除、合并一些特征

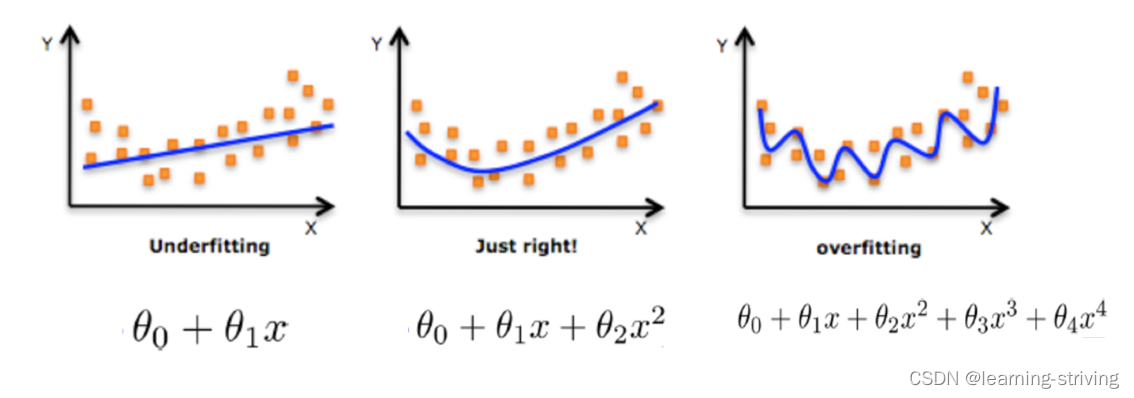
由图可知，应尽量减小高次项特征的影响

在学习的时候，数据提供的特征有些影响模型复杂度或者这个特征的数据点异常较多，所以算法在学习的时候尽量减少这个特征的影响（甚至删除某个特征的影响），这就是正则化

注：调整时候，算法并不知道某个特征影响，而是去调整参数得出优化的结果

2.1 正则化类别

L2正则化

作用：可以使得其中一些W的都很小，都接近于0，削弱某个特征的影响
优点：越小的参数说明模型越简单，越简单的模型则越不容易产生过拟合现象
Ridge回归

L1正则化

作用：可以使得其中一些W的值直接为0，删除这个特征的影响
LASSO回归

三、维灾难

随着维度的增加，分类器性能逐步上升，到达某点之后，其性能便逐渐下降

有一系列猫和狗的图片，通过对猫和狗用一些描述性特征如颜色等构造一个分类器对其进行分类，单个颜色特征可能无法得到一个准确的分类器，需加入一些其他特征，随着特征的增加，分类器性能随之增加，即分类准确率更高，但当特征数量达到一定规模后，分类器性能是下降的

在增加特征过程中，初始时特征越多，分类就越准确，但随着特征维度的增加，样本分布变得越来越稀疏，即过多的特征会导致过拟合现象(训练集上表现良好，对新数据缺乏泛化能力)，要想避免过拟合，需持续增加样本数量

使用更少的特征，能够避免维数灾难的发生，也即避免了高维情况下的过拟合，训练集维度越高，过度拟合风险就越大，训练实例数量随使用的维度数量呈指数增长

扫描二维码关注公众号，回复： 15856638 查看本文章

四、正则化线性模型

4.1 岭回归 (Ridge Regression)

岭回归是线性回归的正则化版本，即在原来的线性回归的 cost function 中添加正则项（regularization term）

$\alpha \sum_{i=1}^{n} \theta_{i}^{2}$

以达到在拟合数据的同时，使模型权重尽可能小的目的,岭回归代价函数

$J(\theta)=M S E(\theta)+\alpha \sum_{i=1}^{n} \theta_{i}^{2}$ ，也即是： $J(\theta)=\frac{1}{m} \sum_{i=1}^{m}\left(\theta^{T} \cdot x^{(i)}-y^{(i)}\right)^{2}+\alpha \sum_{i=1}^{n} \theta_{i}^{2}$

当α=0：岭回归退化为线性回归

4.2 Lasso 回归(Lasso Regression)

Lasso 回归是线性回归的另一种正则化版本，正则项为权值向量的ℓ1范数，Lasso回归的代价函数为

$J(\theta)=\operatorname{MSE}(\theta)+\alpha \sum_{i=1}^{n}\left|\theta_{i}\right|$

Lasso Regression 的代价函数在 $\theta _{i}$ =0处是不可导的
解决方法：在 $\theta _{i}$ =0处用一个次梯度向量(subgradient vector)代替梯度，如下式Lasso Regression 的次梯度向量

$g(\theta, J)=\nabla_{\theta} \operatorname{MSE}(\theta)+\alpha\left(\begin{array}{c} \operatorname{sign}\left(\theta_{1}\right) \\ \operatorname{sign}\left(\theta_{2}\right) \\ \vdots \\ \operatorname{sign}\left(\theta_{n}\right) \end{array}\right) \text { where } \operatorname{sign}\left(\theta_{i}\right)=\left\{\begin{array}{ll} -1 & \text { if } \theta_{i}<0 \\ 0 & \text { if } \theta_{i}=0 \\ +1 & \text { if } \theta_{i}>0 \end{array}\right.$

Lasso Regression 有一个很重要的性质是：倾向于完全消除不重要的权重

例如：当α 取值相对较大时，高阶多项式退化为二次甚至是线性：高阶多项式特征的权重被置为0

也就是说，Lasso Regression 能够自动进行特征选择，并输出一个稀疏模型（只有少数特征的权重是非零的）

4.3 Elastic Net (弹性网络)

弹性网络在岭回归和Lasso回归中进行了折中，通过 混合比(mix ratio) r 进行控制：

r=0：弹性网络变为岭回归
r=1：弹性网络便为Lasso回归

弹性网络的代价函数

$J(\theta)=\operatorname{MSE}(\theta)+r \alpha \sum_{i=1}^{n}\left|\theta_{i}\right|+\frac{1-r}{2} \alpha \sum_{i=1}^{n} \theta_{i}^{2}$

一般来说，我们应避免使用朴素线性回归，而应对模型进行一定的正则化处理

总结

常用的是岭回归
假设只有少部分特征是有用的，则可用弹性网络或Lasso，一般来说，弹性网络的使用更为广泛，因为在特征维度高于训练样本数，或者特征是强相关的情况下，Lasso回归的表现不太稳定
api：from sklearn.linear_model import Ridge, ElasticNet, Lasso
除了上述三种，Early Stopping 也是正则化迭代学习的方法之一，其做法为：在验证错误率达到最小值的时候停止训练

五、线性回归的改进-岭回归api使用

sklearn.linear_model.Ridge(alpha=1.0, fit_intercept=True,solver="auto", normalize=False)：具有l2正则化的线性回归
- alpha：正则化力度，也叫 λ，λ取值为0~1 ，1~10
- solver：会根据数据自动选择优化方法
  - sag:如果数据集、特征都比较大，选择该随机梯度下降优化
- normalize：数据是否进行标准化
  - normalize=False：可以在fit之前调用preprocessing.StandardScaler标准化数据
- Ridge.coef_：回归权重
- Ridge.intercept_：回归偏置
Ridge方法相当于SGDRegressor(penalty='l2', loss="squared_loss"),只不过SGDRegressor实现了一个普通的随机梯度下降学习，推荐使用Ridge(实现了SAG)
sklearn.linear_model.RidgeCV(_BaseRidgeCV, RegressorMixin)：具有l2正则化的线性回归，可以进行交叉验证
- coef_:回归系数

正则化函数的岭系数变化如下

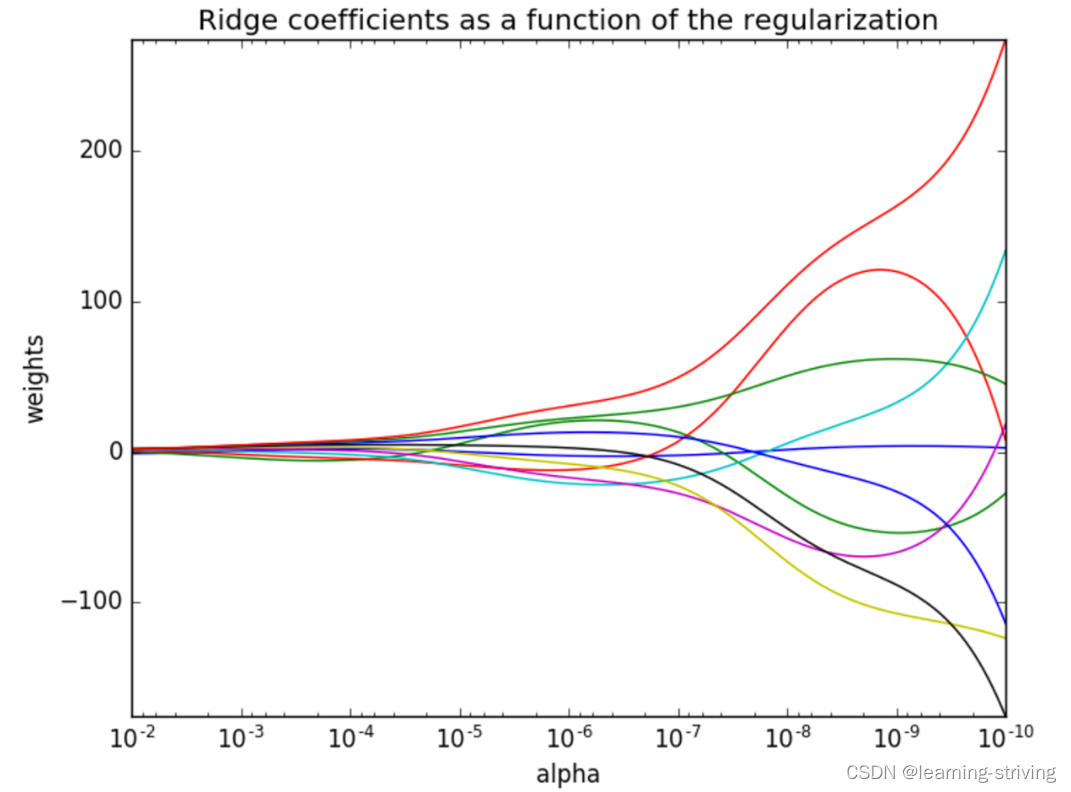
正则化力度越大，权重系数会越小
正则化力度越小，权重系数会越大

from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import Ridge, RidgeCV   # 导入模块
from sklearn.metrics import mean_squared_error

def linear_model():     # 线性回归:岭回归

    # 1.获取数据
    data = load_boston()
    # 2.数据集划分
    x_train, x_test, y_train, y_test = train_test_split(data.data, data.target, random_state=22)
    # 3.特征工程-标准化
    transfer = StandardScaler()
    x_train = transfer.fit_transform(x_train)
    x_test = transfer.fit_transform(x_test)
    # 4.机器学习-线性回归(岭回归)
    estimator = Ridge(alpha=1)
    # estimator = RidgeCV(alphas=(0.001, 0.1, 1, 10, 100))
    estimator.fit(x_train, y_train)
    # 5.模型评估
    # 5.1 获取系数等值
    y_predict = estimator.predict(x_test)
    print("预测值为:\n", y_predict)
    print("模型中的系数为:\n", estimator.coef_)
    print("模型中的偏置为:\n", estimator.intercept_)
    # 5.2 评价
    # 均方误差
    error = mean_squared_error(y_test, y_predict)
    print("误差为:\n", error)

if __name__ == '__main__':
    linear_model()
---------------------------------------------------------
输出：
预测值为:
 [28.13514381 31.28742806 20.54637256 31.45779505 19.05568933 18.26035004
 20.59277879 18.46395399 18.49310689 32.89149735 20.38916336 27.19539571
 14.82641534 19.22385973 36.98699955 18.29852297  7.78481347 17.58930015
 30.19228148 23.61186682 18.14688039 33.81334203 28.44588593 16.97492092
 34.72357533 26.19400705 34.77212916 26.62689656 18.63066492 13.34246426
 30.35128911 14.59472585 37.18259957  8.93178571 15.10673508 16.1072542
  7.22299512 19.14535184 39.53308652 28.26937936 24.62676357 16.76310494
 37.85719041  5.71249289 21.17777272 24.60640023 18.90197753 19.95020929
 15.1922374  26.27853095  7.55102357 27.10160025 29.17947182 16.275476
  8.02888564 35.42165713 32.28262473 20.9525814  16.43494393 20.88177884
 22.92764493 23.58271167 19.35870763 38.27704421 23.98459232 18.96691367
 12.66552625  6.122414   41.44033214 21.09214394 16.23412117 21.51649375
 40.72274345 20.53192898 36.78646575 27.01972904 19.91315009 19.66906691
 24.59629369 21.2589005  30.93402996 19.33386041 22.3055747  31.07671682
 26.39230161 20.24709071 28.79113538 20.85968277 26.04247756 19.25344252
 24.9235031  22.29606909 18.94734935 18.83346051 14.09641763 17.43434945
 24.16599713 15.86179766 20.05792005 26.51141362 20.11472351 17.03501767
 23.83611956 22.82305362 20.88305157 36.10592864 14.72050619 20.67225818
 32.43628539 33.17614341 19.8129561  26.45401305 20.97734485 16.47095097
 20.76417338 20.58558754 26.85985053 24.18030055 23.22217136 13.7919355
 15.38830634  2.78927979 28.87941047 19.80046894 21.50479706 27.53668749
 28.48598562]
模型中的系数为:
 [-0.63591916  1.12109181 -0.09319611  0.74628129 -1.91888749  2.71927719
 -0.08590464 -3.25882705  2.41315949 -1.76930347 -1.74279405  0.87205004
 -3.89758657]
模型中的偏置为:
 22.62137203166228
误差为:
 20.064724392806898

六、sklearn模型的保存和加载API

导入模块：from sklearn.externals import joblib # 已失效
使用import joblib
- 保存：joblib.dump(estimator, 'test.pkl')
- 加载：estimator = joblib.load('test.pkl')

线性回归的模型保存加载案例

from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import Ridge, RidgeCV   # 导入模块
from sklearn.metrics import mean_squared_error
# from sklearn.externals import joblib   # 无效，改用下行导入
import joblib

def load_dump_demo():     # 线性回归:岭回归

    # 1.获取数据
    data = load_boston()
    # 2.数据集划分
    x_train, x_test, y_train, y_test = train_test_split(data.data, data.target, random_state=22, test_size=0.2)
    # 3.特征工程-标准化
    transfer = StandardScaler()
    x_train = transfer.fit_transform(x_train)
    x_test = transfer.fit_transform(x_test)

    # 4.机器学习-线性回归(岭回归)
    # 4.1 模型训练
    # estimator = Ridge(alpha=1)
    # estimator.fit(x_train, y_train)
    # # 4.2 模型保存
    # joblib.dump(estimator, "./test.pkl")

    # 4.3 模型加载
    estimator = joblib.load("./test.pkl")   # 先运行注释代码进行模型保存，注释后再运行该行代码

    # 5.模型评估
    # 5.1 获取系数等值
    y_predict = estimator.predict(x_test)
    print("预测值为:\n", y_predict)
    print("模型中的系数为:\n", estimator.coef_)
    print("模型中的偏置为:\n", estimator.intercept_)

    # 5.2 评价
    # 均方误差
    error = mean_squared_error(y_test, y_predict)
    print("误差为:\n", error)


if __name__ == '__main__':
    load_dump_demo()
-------------------------------------------------------------------------
输出：  # 运行4.1,4.2
预测值为:
 [27.78873457 30.88050916 20.7278544  31.57167054 18.75977878 18.46287435
 20.719399   18.02915627 18.21657378 32.22520354 20.47916624 27.2511531
 15.05294942 19.27076022 36.15980162 18.42723014  7.79369197 17.3680282
 29.41241038 23.3281782  18.43319722 33.27590755 28.35135334 17.41391778
 34.21591336 26.0296379  34.5838712  26.07766082 19.11301251 12.78779461
 29.97371042 14.61585424 36.81099837  9.12517646 15.10411068 16.64292828
  8.01158958 19.38880315 39.11889581 27.46040948 24.24640334 16.94638444
 38.04105813  6.62389382 21.47631033 24.37881408 18.9059369  19.89761521
 15.7132391  26.46605334  8.2025957  26.86177914 29.18720561 16.85456495
  8.49458658 34.83395243 32.30959733 20.61181045 16.29762508 20.34090122
 22.830845   23.43394661 19.05120909 37.44873593 23.7104196  19.41216025
 13.00521048  6.97818359 40.99752892 20.87747386 16.7024726  20.82862838
 39.88275744 20.24968244 36.11441189 26.7758095  19.31349113 19.6245034
 24.0553401  20.6065828  30.48446232 19.0989152  22.55823821 30.74827306
 26.23282983 20.46955834 28.50915212 20.20310585 25.96357801 19.03376439
 24.9380452  22.82851545 19.181656   18.93235434 14.50560797 17.77224626
 23.97068811 16.0106808  20.47816964 26.18277209 20.61876916 17.35873382]
模型中的系数为:
 [-0.71845222  1.10899367 -0.16686116  0.86602377 -1.99228506  2.73072103
 -0.16588061 -3.32715968  2.48093423 -1.60572264 -1.66849991  0.91120104
 -3.78188807]
模型中的偏置为:
 22.57970297029704
误差为:
 20.945827015197693
-----------------------------------
加载已保存模型运行结果为：  # 即运行4.3
……    # 省略，由输出可知结果相同
模型中的系数为:
 [-0.71845222  1.10899367 -0.16686116  0.86602377 -1.99228506  2.73072103
 -0.16588061 -3.32715968  2.48093423 -1.60572264 -1.66849991  0.91120104
 -3.78188807]
模型中的偏置为:
 22.57970297029704
误差为:
 20.945827015197693

学习导航：http://xqnav.top/