目录
前言：
回溯算法是一个比较抽象的算法，因此我们如果初学者，难度可以说是非常大，因此我们利用这篇来讲解回溯算法的理论知识，后续在力扣刷题里面也会详细介绍回溯算法的相关例题。
回溯算法：
回溯算法是一种常见的求解问题的算法。它通常被用来在大量的解空间中搜索所有可能的解，找到所需的解或最优解。
回溯算法通常使用递归来实现。在回溯算法中，递归函数用于在候选解空间中搜索所有可能的解。
回溯算法将问题分解为许多子问题，并递归地对每个子问题进行求解。通过回溯和剪枝，可以避免不必要的计算，提高算法效率。每当算法解决了一个子问题时，它需要回溯到上一个状态，再求解下一个子问题。
因此，回溯算法与递归有密切的关系。实现回溯算法的一种常见方法是使用递归来穷举所有可能的解。递归函数中的状态变量可以充当回溯的历史状态，以便在必要时将其还原到以前的状态。
回溯算法工作流程如下：
1. 定义问题的解空间:定义问题的解空间，并决定要寻找哪些变量或解。
2. 约束条件:针对解空间中的每个子集进行约束条件。
3. 构建候选解:构建候选解。
4. 检查约束:检查每个候选解是否满足约束条件。
5. 解决或回溯:如果候选解满足约束条件，则保存解并继续构建更多解。如果候选解不满足约束条件，则回溯到前一个状态，并继续构建其他候选解。这个过程一直进行，直到找到所需的解或所有的解都被考虑过。
回溯算法常常用于组合优化问题，如旅行商问题、八皇后问题、数独等。其时间复杂度通常为指数级别，因此在解空间较大时，需要谨慎使用。
回溯搜索法其实就是一个纯暴力的搜索，主要是因为部分问题实在太过于复杂，此时使用回溯法暴力搜索如果可以搜索出来就已经是很好的结果了。
回溯算法的特点：
- 穷举搜索：回溯算法会尝试所有可能的解，因此可以找到所有满足条件的解。
- 适用范围广：回溯算法可以用于求解组合优化问题、排列组合问题、子集划分问题等各种问题。
- 可以剪枝优化：通过剪枝操作，可以减少无效的搜索，提高算法的效率。
然而，回溯算法的时间复杂度通常很高，因为它需要遍历大量的可能解。在实际应用中，为了减小搜索空间，可以结合其他优化技巧，如剪枝、启发式搜索等。
启发式搜索：
启发式搜索（Heuristic Search）是一种通过使用启发信息来引导搜索方向的搜索算法。它针对问题的特定特征和启发信息（也称为估价函数、启发函数或评估函数），在搜索过程中选择最有希望的路径来达到目标。
在传统的搜索算法中，如深度优先搜索和广度优先搜索，是盲目地按照某种搜索策略进行搜索，没有充分利用问题本身的特征信息。而启发式搜索不同，它使用问题的特定启发信息来评估搜索状态的优劣性，并根据启发信息指导搜索方向。
启发函数给出了当前搜索状态的一个估计值，表示该状态与目标之间的距离或优劣程度。通过比较不同状态的启发函数值，启发式搜索算法可以选择具有更优启发函数值的状态作为下一步的搜索目标。这样做的目的是尽量将搜索方向朝向更有希望接近目标的位置。
回溯法的常见应用:
回溯算法通常用于求解组合优化问题。组合优化问题的特点是：在给定一组变量的情况下，需要找到满足一定约束条件的最优解或所有解。
回溯算法常用于解决切割字符串问题，例如如何切割字符串使得切割结果都是回文子串。
回溯算法常用于解决子集问题，求一个集合的所有子集。
回溯算法常用于解决排列问题
回溯法常用于解n皇后，数独问题。
回溯法的模板:
void backtrack(vector<int>& path, vector<int>& choices) {
// 满足结束条件，处理结果并返回
if (满足结束条件) {
处理结果
return;
}
for (int i = 0; i < choices.size(); i++) {
int choice = choices[i];
// 跳过无效选择
if (选择不满足约束条件) {
continue;
}
// 选择当前路径
做出选择
path.push_back(choice);
// 进入下一层决策树
backtrack(path, choices);
// 撤销选择
撤销选择
path.pop_back();
}
}
在使用时，需要根据具体问题自行定义结束条件、约束条件、处理结果和选择操作。在backtrack函数中，将问题的路径存储在path中，choices为当前可选择的选项。
需要注意的是，上述模板中的具体代码需要根据实际问题进行实现，包括判断结束条件、约束条件、做出选择和撤销选择等操作。
回溯法的图解：
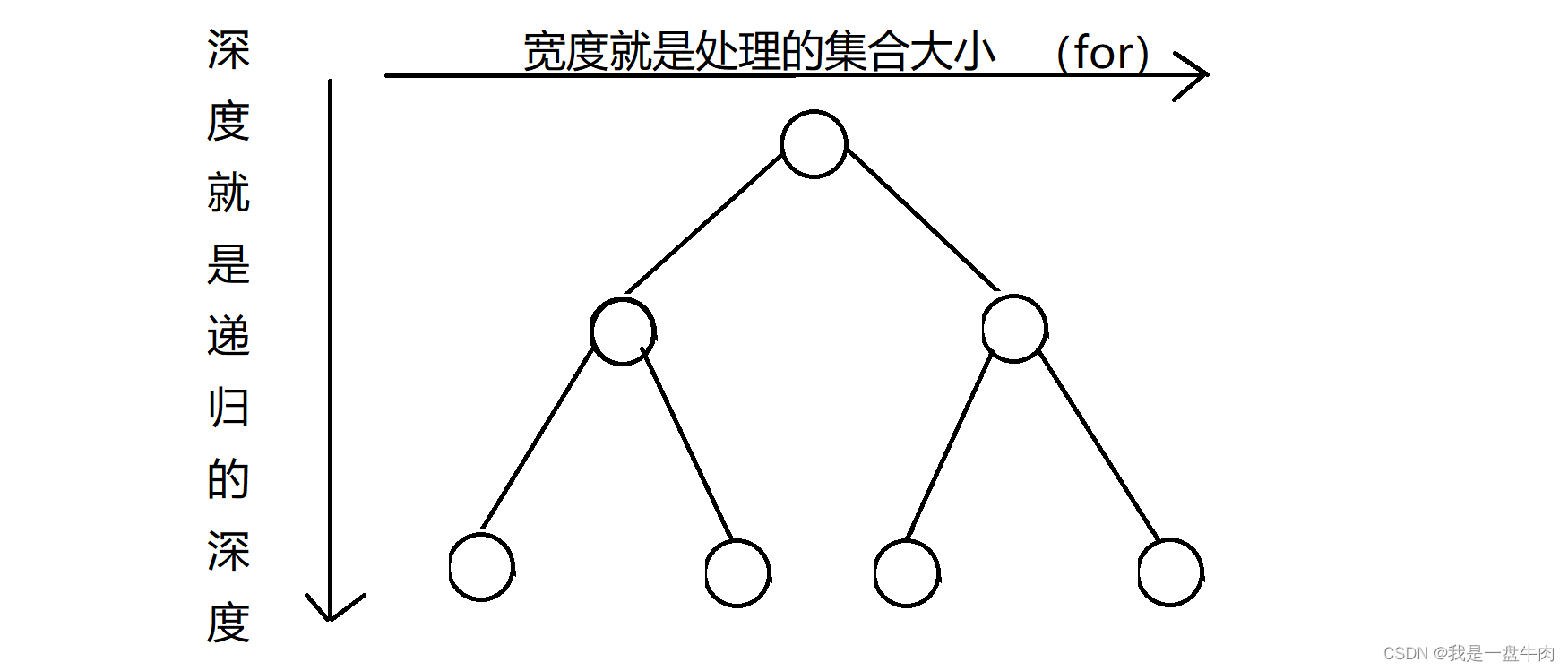
回溯可以看作一个N叉树结构，因为它的运行过程可以用树的方式进行描述和可视化。
在回溯算法中，我们通过尝试不同的选择和路径来解决问题，直到找到可行的解决方案或者确定无解。这个过程可以看作是在一个多叉树中不断搜索的过程。
下面以一个经典的例子来说明回溯算法的树结构表示：
假设我们要解决一个迷宫问题，迷宫由一个起点和一个终点组成，中间有若干个墙壁。我们可以选择上下左右四个方向中的一个方向前进，直到到达终点或者无路可走。
首先，我们在起点开始，向四个方向中的一个前进，得到四个子节点，分别代表向上、向下、向左、向右四个方向的移动。
对于每个子节点，我们再次尝试向四个方向中的一个前进，得到八个子节点。
以此类推，我们不断生成新的子节点，直到到达终点或者无路可走。
整个过程可以看作是一个树的遍历过程，每个节点代表一个状态，代表当前所在的位置和已经走过的路径。树的根节点是初始状态，叶子节点是最终的解决方案。
此外，回溯算法的树结构还具有回溯的特点，即在搜索过程中，如果发现当前选择导致了无解或者不可行的情况，就返回上一层，撤销当前选择，重新尝试其他选择。这种撤销和回退的操作也可以通过树的退回到上一层的操作来表示。
因此，回溯算法的运行过程可以看作是在一个树结构中进行搜索和回退的过程，通过遍历树的节点来得到问题的解。
案例：
77. 组合 - 力扣（LeetCode）
给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。
你可以按 任何顺序 返回答案。
这道题其实还是可以用for循环来做，但是问题在于要返回几个数的组合，就要写几个for循环，因为返回几个数是由我们自己决定的。如何控制for循环的个数，就成了本题的关键，而本题给出的方法就是回溯算法。
需要注意的是组合不是排列，组合中[1,2]和[2,1]是一个组合，这也是为什么我们下面2，3，4节点只取后续节点而不往前取。
我们在这里先用图讲解一下基本思路（1234组合，取两个数字作为集合）：
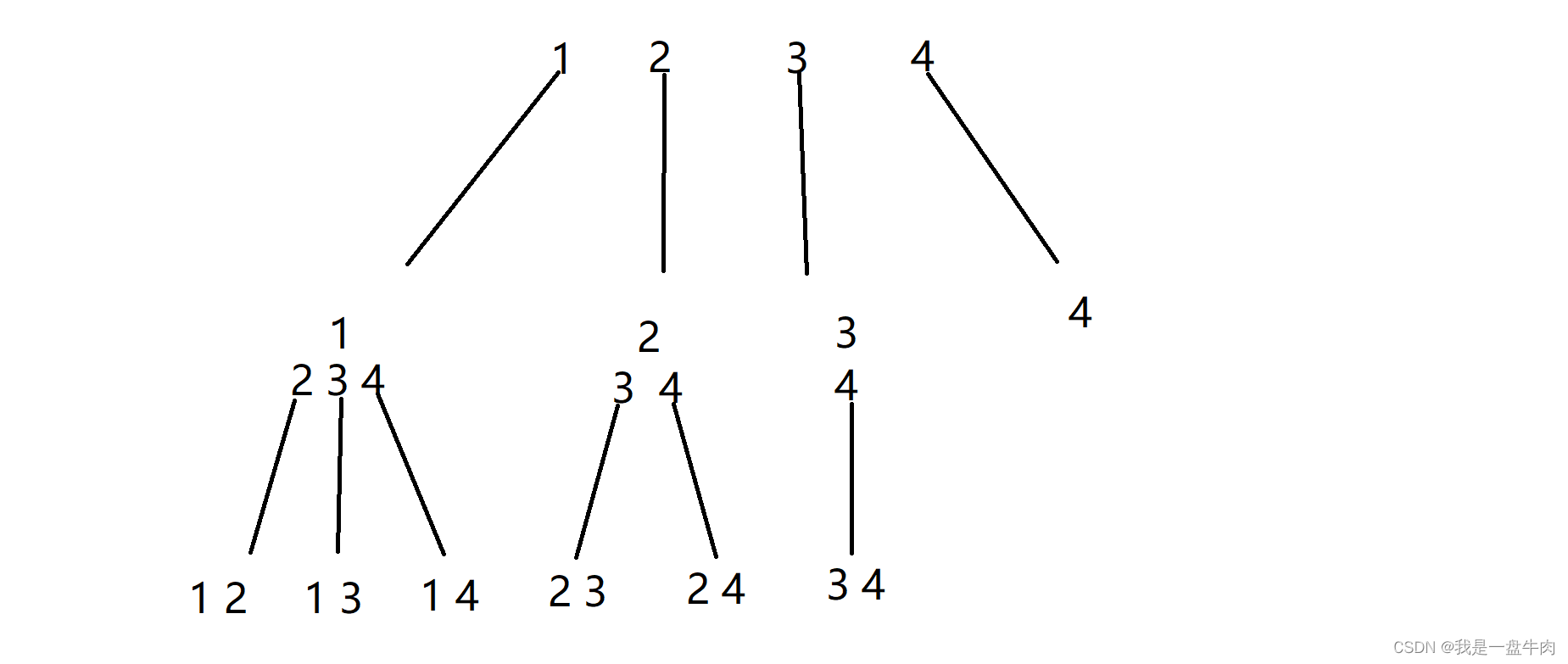回溯的过程就是：我们以 1 节点为例，1向下取 12 满足条件，回溯到1，再取13 满足条件 回溯到1，再取14，满足条件，此时1节点已经满足需求了，因此我们在回溯，到初始节点，选择2在进行上述步骤。
class Solution {
private:
vector<vector<int>> result; // 存放符合条件结果的集合
vector<int> path; // 用来存放符合条件结果
void backtracking(int n, int k, int startIndex) {
if (path.size() == k) {
result.push_back(path);
return;
}
for (int i = startIndex; i <= n; i++) {
path.push_back(i); // 处理节点
backtracking(n, k, i + 1); // 递归
path.pop_back(); // 回溯，撤销处理的节点
}
}
public:
vector<vector<int>> combine(int n, int k) {
backtracking(n, k, 1);
return result;
}
};总结：
回溯算法实际上就是递归和for循环的组合，利用递归来自定义了for循环的个数，是一个很不错的思路，并且回溯算法也有自己比较固定的模板，我们在写的时候可以根据这个模板来确定大体框架，补全框架细节，就能得到利用回溯苏纳法解决问题的代码。
如果我的内容对你有帮助，请点赞，评论，收藏。创作不易，大家的支持就是我坚持下去的动力！
