概述
变分模态分解由Konstantin Dragomiretskiy于2014年提出,可以很好抑制EMD方法的模态混叠现象(通过控制带宽来避免混叠现象)。
与EMD原理不同,VMD分解方式是利用迭代搜索变分模型最优解来确定每个分解的分量中心频率及带宽,属于完全非递归模型,该模型寻找模态分量的集合及其各自的中心频率,而每个模态在解调成基带之后是平滑的。
Konstantin Dragomiretskiy通过实验结果证明:对于采样和噪声方面,该方法更具有鲁棒性。
模态变分分解是一种自适应、完全非递归的模态变分和信号处理的方法。该技术具有可以确定模态分解个数的优点,其自适应性表现在根据实际情况确定所给序列的模态分解个数.
随后的搜索和求解过程中可以自适应地匹配每种模态的最佳中心频率和有限带宽,并且可以实现固有模态分量(IMF)的有效分离、信号的频域划分、进而得到给定信号的有效分解成分,最终获得变分问题的最优解。
它克服了EMD方法存在端点效应和模态分量混叠的问题,并且具有更坚实的数学理论基础,可以降低复杂度高和非线性强的时间序列非平稳性,分解获得包含多个不同频率尺度且相对平稳的子序列,适用于非平稳性的序列,VMD的核心思想是构建和求解变分问题。
构造变分问题
假设原始信号f被分解为k个分量,保证分解序列为具有中心频率的有限带宽的模态分量,同时各模态的估计带宽之和最小,约束条件为所有模态之和与原始信号 相等,则VMD约束变分模型如下:

其中,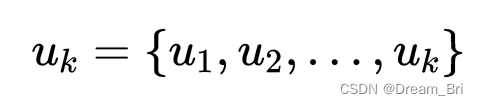
为各模态函数,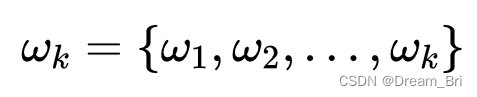
为各模态中心频率。
变分求解问题(引入拉格朗日)
解决上述的约束最优化问题,将约束变分问题转变为非约束变分问题,利用二次惩罚项和拉格朗日乘子法的优势,引入了增广拉格朗日(Lagrangian)函数,如式所示:
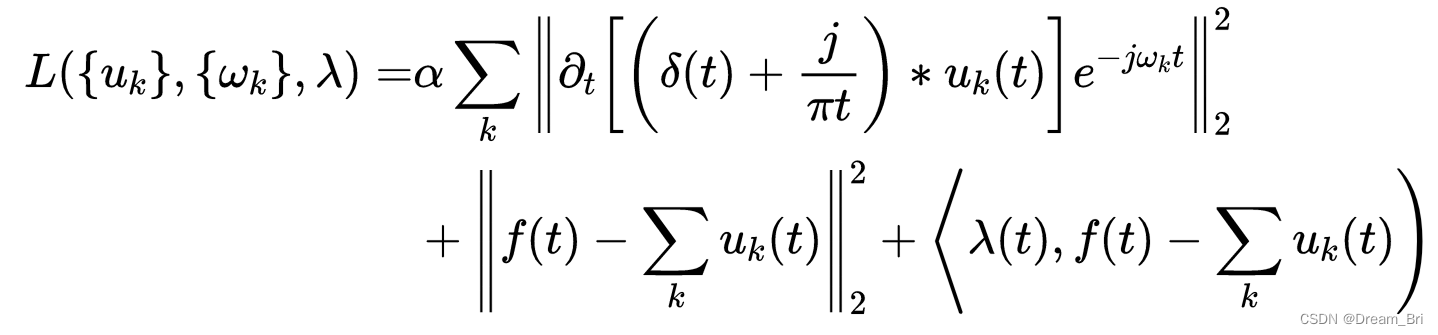
其中, α \alpha α是罚参数, λ \lambda λ是Lagrangian乘子。
对于所有 ω \omega ω>=0,更新泛函
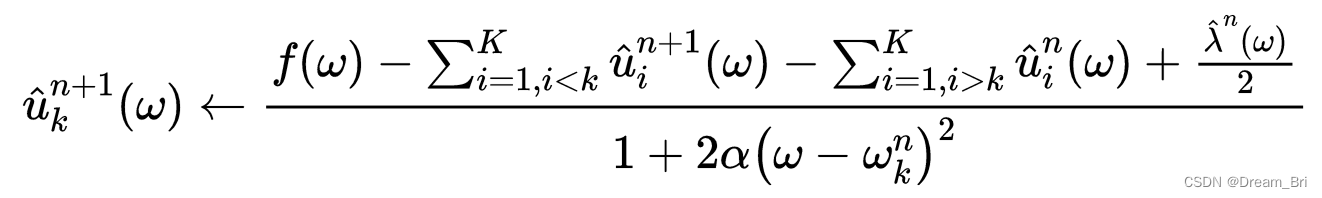
更新泛函 ω \omega ωk:
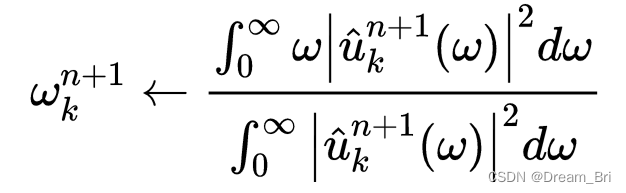
所有 ω \omega ω>=0,进行双重提升:
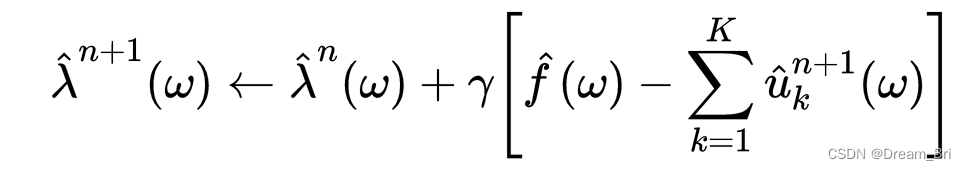
γ \gamma γ表示噪声,当信号含有强噪声时,可以设定 γ \gamma γ=0达到更好的去噪效果。
不断重复更新泛函,知道满足下面的迭代约束条件:
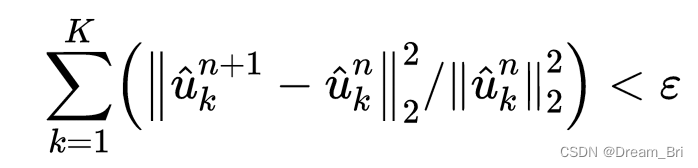
对于所有的 ω \omega ω>=0 —>解析信号的单边谱只包含非负频率。
以上过程的程序框图如下:
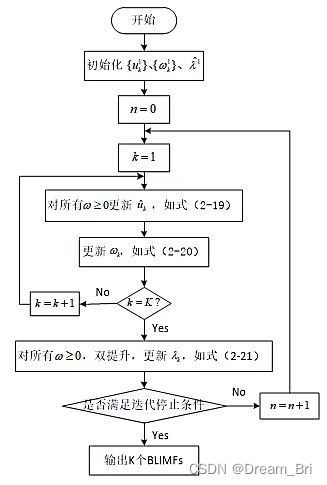
文字解释:
1、初始化uk、ωk、λ和n=0,k=0
2、n=n+1(迭代次数)
3、k=k+1,根据VMD算法公式更新uk、ωk
4、又根据相关的算法更新拉格朗日乘数λ
5、知直到满足一定条件,停止迭代,不然转到2步骤
以上便是求解每一个模态的单步骤
关于变分构造中的函数理解
变分构造函数如下:
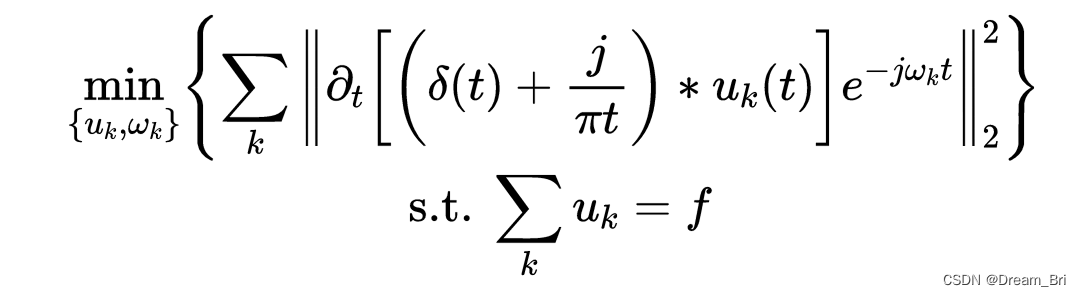
关于Uk(t)
有如下定义:
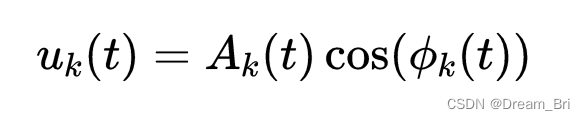

关于希尔伯特变换
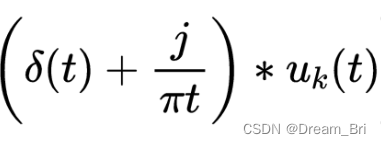
希尔伯特变换:

上面的Hilbert变换的表达式实际上就是将原始信号和一个信号做卷积的结果。因此,Hilbert变换可以看成是将原始信号通过一个滤波器,或者一个系统,这个系统的冲击响应为h(t)。
希尔伯特变换的意义:
信号通过Hilbert变换后,正频率部分乘以-j,也就是说,保持幅度不变的条件下,将相位移动了-π/2,而对于负频率成分,移动了π/2,因此Hilbert变换又称为90°相移滤波器或者垂直滤波器。
希尔伯特变换下的解析信号意义:首先,将实数信号变换成解析信号的结果就是,把一个一维的信号变成了二维复平面上的信号,复数的模和幅角代表了信号的幅度和相位,如图所示:

关于频谱调制
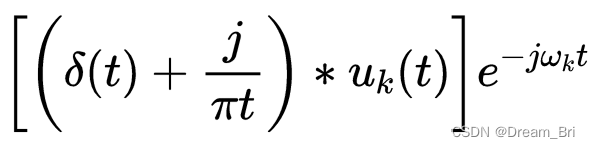
此处采用了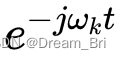
来调节每个模态的频谱,使之调制到相应的基频带。
调制定理:
调制信号在时域成以一个等幅高频振荡,相当于在频域把调制信号的各频率分量均搬至高频振荡的频率上,调制信号的各频率分量幅度减半。
所用到的基本式子如下:
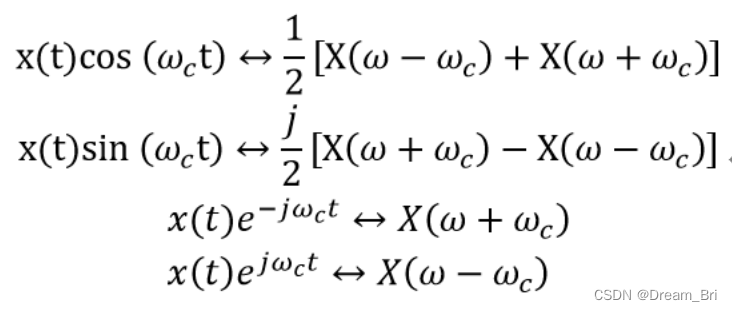
VMD算法(python)
代码程序:
import numpy as np
import matplotlib.pyplot as plt
from vmdpy import VMD
# Time Domain 0 to T
T = 1000
fs = 1/T
t = np.arange(1,T+1)/T#通过指定起始值和终值来创建一维数组
freqs = 2*np.pi*(t-0.5-fs)/(fs)
# center frequencies of components
f_1 = 2
f_2 = 20
f_3 = 40
# modes
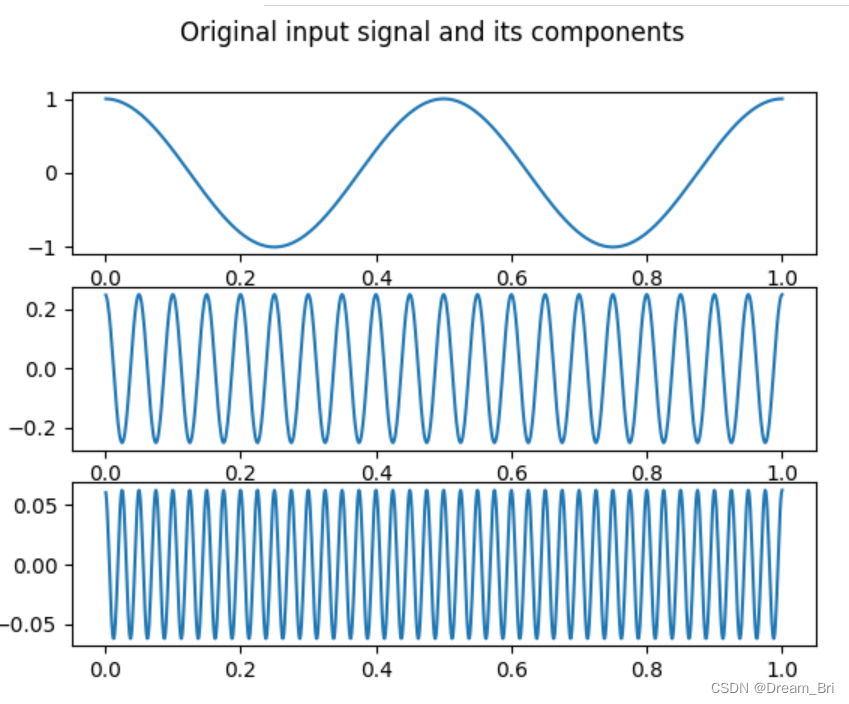
v_1 = (np.cos(2*np.pi*f_1*t))
v_2 = 1/4*(np.cos(2*np.pi*f_2*t))
v_3 = 1/16*(np.cos(2*np.pi*f_3*t))
#% for visualization purposes
fsub = {
1:v_1,2:v_2,3:v_3}
wsub = {
1:2*np.pi*f_1,2:2*np.pi*f_2,3:2*np.pi*f_3}
# composite signal, including noise
f1=v_1 + v_2 + v_3
f = v_1 + v_2 + v_3 + 0.1*np.random.randn(v_1.size)
f_hat = np.fft.fftshift((np.fft.fft(f)))
fig1 = plt.figure()
plt.xlim((0,1))
for key, value in fsub.items():
plt.subplot(3,1,key)
plt.plot(t,value)
fig1.suptitle('Original input signal and its components')
# some sample parameters for VMD
alpha = 2000
tau = 0.
K = 3
DC = 0
init = 1
tol = 1e-7
# Run actual VMD code
u, u_hat, omega = VMD(f, alpha, tau, K, DC, init, tol)
# Simple Visualization of decomposed modes
plt.figure()
plt.plot(u.T)
plt.title('Decomposed modes')
fig4 = plt.figure()
plt.loglog(freqs[T//2:], abs(f_hat[T//2:]), 'k:')
plt.xlim(np.array([1, T//2])*np.pi*2)
for k in range(K):
plt.loglog(freqs[T//2:], abs(u_hat[T//2:,k]), linestyles[k])
#plt.plot(freqs[T // 2:], abs(u_hat[T // 2:, k]), linestyles[k])
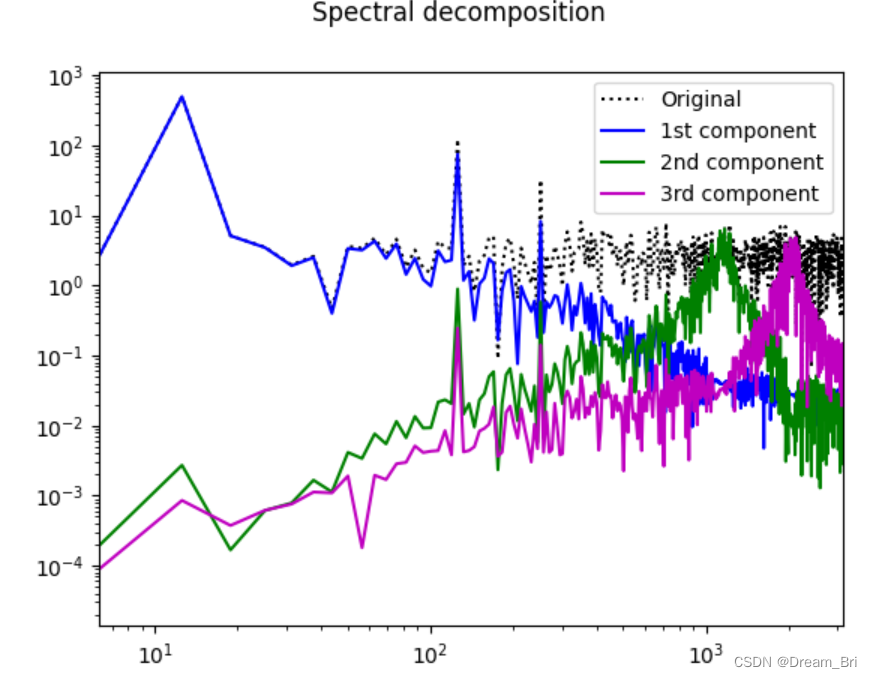
fig4.suptitle('Spectral decomposition')
plt.legend(['Original','1st component','2nd component','3rd component'])
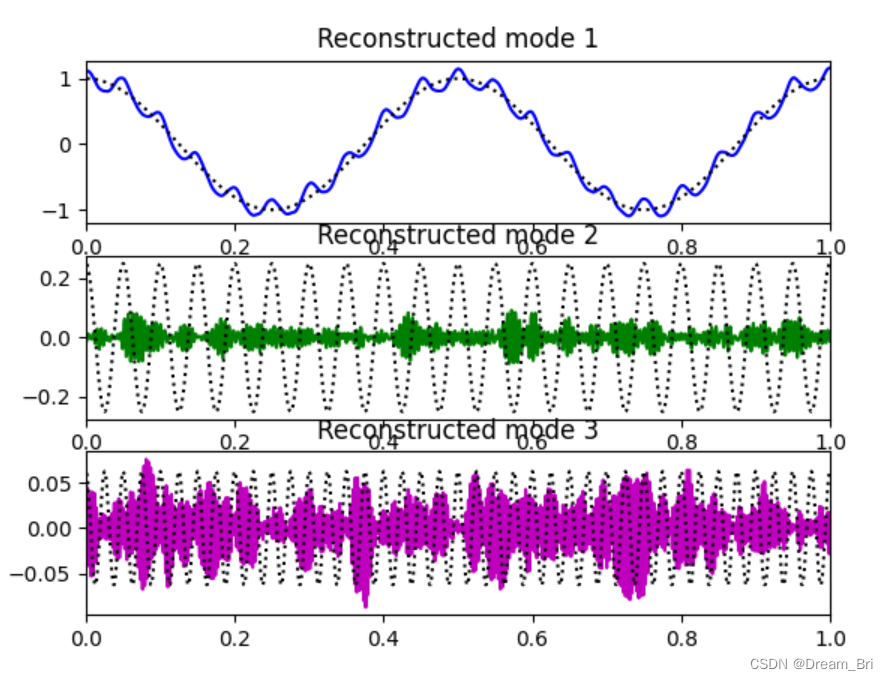
fig5 = plt.figure()
for k in range(K):
plt.subplot(3,1,k+1)
plt.plot(t,u[k,:], linestyles[k])
plt.plot(t, fsub[k+1], 'k:')
plt.xlim((0,1))
plt.title('Reconstructed mode %d'%(k+1))
plt.show()
程序显示:

参考:
https://blog.csdn.net/SparkQiang/article/details/103498160
https://blog.csdn.net/arm_qiao/article/details/108482727