提升方法采用加法模型(即基函数的线性组合)与前向分步算法。以决策树为基 函数的提升方法称为提升树(boosting tree)。对分类问题决策树是二叉分类树,对回归 问题决策树是二叉回归树。在AdaBoost的案例中看到的基本分类器x<v或x>v,可以看作是由一个根 结点直接连接两个叶结点的简单决策树,即所谓的决策树桩(decision stump)。
提升树 模型可以表示为决策树的加法模型:

提升树算法:
提升树算法采用前向分步算法。首先确定初始提升树f 0(x)=0,第m歩的模型是:
![]()
其中,fm-1(x)为当前模型,通过经验风险极小化确定下一棵决策树的参数Θm,

下面讨论针对不同问题的提升树学习算法,其主要区别在于使用的损失函数不同。包 括用平方误差损失函数的回归问题,用指数损失函数的分类问题,以及用一般损失函数的 一般决策问题。
对于二类分类问题,提升树算法只需将AdaBoost算法中的基本分类器限制为二类 分类树即可,可以说这时的提升树算法是AdaBoost算法的特殊情况,这里不再细述。下面 叙述回归问题的提升树。

回归问题提升树使用以下前向分步算法:
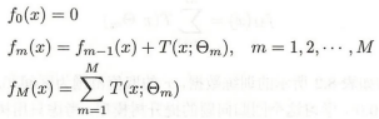
在前向分步算法的第m步,给定当前模型fm-1(x),需求解:

得到 m,即第m棵树的参数。
当采用平方误差损失函数时,
![]()
其损失变为:

这里,![]() 是当前模型拟合数据的残差(residual)。
是当前模型拟合数据的残差(residual)。
所以,对回归问题的提升树算法来说,只需简 单地拟合当前模型的残差。这样,算法是相当简单的。

案例:
已知如表8.2所示的训练数据,x的取值范围为区间[0.5,10.5],y的取值范围为 区间[5.0,10.0],学习这个回归问题的提升树模型,考虑只用树桩作为基函数。

解:
(1)第1步求f 1(x)即回归树T1(x)。
首先通过以下优化问题,求解训练数据的切分点s:

![]()
容易求得在R1,R2内部使平方损失误差达到最小值的c1,c2。

这里N1,N2是R1,R2的样本点数。
求训练数据的切分点。
根据所给数据,考虑如下切分点: 1.5,2.5,3.5,4.5,5.5,6.5,7.5,8.5,9.5
对各切分点,不难求出相应的R1,R2,c1,c2及
![]()
例如,当s=1.5时,R1={1},R2={2,3,…,10},c1=5.56,c2=7.50,
![]()
现将s及m(s)的计算结果列表如下(见表8.3)

由表8.3可知,当s=6.5时m(s)达到最小值,此时R1={1,2,…,6},R2= {7,8,9,10},c1 =6.24,c2=8.91,所以回归树T1(x)为

以上就是求解回归树的标准流程。
(2)第二轮:
用f 1(x)拟合训练数据的残差见表8.4,表中r 2i=yi-f 1(xi),i=1,2,…,10。

计算出用f 1(x)拟合训练数据得到的模型的平方损失误差:

第2步求T2(x)。方法与求T1(x)一样,只是拟合的数据是表8.4的残差。可以得到:

用f 2(x)拟合训练数据的平方损失误差是:

继续求得:

用f 6(x)拟合训练数据的平方损失误差是:

假设此时已满足误差要求,那么f(x)=f 6(x)即为所求提升树。
梯度提升算法:
提升树利用加法模型与前向分歩算法实现学习的优化过程。当损失函数是平方损失和 指数损失函数时,每一步优化是很简单的。但对一般损失函数而言,往往每一步优化并不 那么容易。针对这一问题,Freidman提出了梯度提升(gradient boosting)算法。这是利用 最速下降法的近似方法,其关键是利用损失函数的负梯度在当前模型的值

作为回归问题提升树算法中的残差的近似值,拟合一个回归树。
算法:

解释:
(1)初始化一个最初的模型,用下面优化公式估计一个能使损失比较小的常数值c,这个常数值相当于一个只有单一根节点的树的模型。

(2)计算当前模型的损失函数的负梯度的值,将它作为残差的估计。对于平方损失函 数,它就是通常所说的残差;对于一般损失函数,它就是残差的近似值。

(3)有了残差,用残差来作为输入来进行回归树的切分,就是执行之前讲过的标准的回归决策树的切分流程,进行本次切分。得到的这次回归树就是c,下面公式就是这个意思.

因此就得到了该轮的模型:
这一次的切分得到的最优子数记为Cm,加上之前数轮的模型就是当前轮得到的回归树的模型。

前面的由Cm得到的模型就是,

就是回归树的模型。
(4)M轮的循环之后,最终得到回归树模型:
