引言
如果您刚刚接触傅里叶变换,不要害怕。傅里叶变换的原理和应用可能会有些抽象和难以理解,但是只要有耐心和恒心,学习傅里叶变换还是非常有意义和值得的。本篇博客将会介绍傅里叶变换的基础概念和应用。
情景引入
设想你正走在一个嘈杂的菜市场里,耳边传来各种各样的声音。如果你仔细分辨,就可以慢慢分辨出来其中有小贩的叫卖声,有小孩子的哭闹声,有讨价还价的声音等等。傅里叶变换和这个情景非常类似,就是将一个复杂的信号在时间域和频率域之间进行转换。将你耳朵里听到的声波视作原始数据,那么傅里叶变换就是将这个复杂的声波转换成多个周期性的声波。
概念
对于傅里叶变换,我们 需要了解两个概念,一个是傅里叶级数,一个是傅里叶变换。我们先从傅里叶级数开始说起
傅里叶级数
高中里我们知道,将两个或者多个正(余)弦函数函数相加减,得到的结果也是周期性函数。例如我将Sin(x)和Cos(x)相加,得到的结果还是周期性函数。那么问题来了,对于任意一个周期性函数,能不能将其拆分成由多个正(余)弦函数的和呢?傅里叶发现是可以的。(具体怎么证明是可以的大家就自行了解吧)
所以这里引出了傅里叶级数的定理:任何一个周期函数都可以表示为一组正弦和余弦函数的级数。
具体来说,设f(x) 为一个周期为 T 的函数,则它的傅里叶级数可表示为:

看上去很复杂,将其用正弦表达并化简就变成:
![]()
当然也可以将其用余弦表达。
因此我们就得到了三个东西,一个振幅c,一个ω可以认为是周期(真正周期为2π除以ω),一个相位ф。
如果以时间为x轴,函数值为y轴,绘制图像,那么我们可以得到这个函数(波)随着时间的推移呈现出周期性变化的图像(其实也就是原函数图像),我们称之为时域。
用图像示意一下。

三个波合成为一个波,就会得到一个新的周期性函数,下图红色的线就是新的周期性函数。红色的波由以上三种波合成。可以被分解为以上的三个波。

而如果以振幅c为y轴,以ω作为x轴,那么我们就可以画出一个柱形图。表示分成了几个波,每隔波的振幅又是多少,这个柱形图就被称为频域。与此同时,如果在这个柱形图中加入相位数据,就可以得到一个三维的图。
图像示意一下

代码示意:
附上一小段代码,如何绘制上图,大家不用看也行,主要是介绍python怎么实现傅里叶变换的一个demo:
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# 生成测试数据(一个带有多个频率分量的正弦波信号)
t = np.linspace(0, 1, 1000)
y = 5 * np.sin(2*np.pi*10*t) + 2 * np.sin(2*np.pi*30*t) + 3 * np.sin(2*np.pi*60*t)
# 傅里叶变换得到振幅和相位信息
freqs = np.fft.fftfreq(len(t), t[1]-t[0])
fft_vals = np.fft.fft(y)
amps = np.abs(fft_vals)
phases = np.angle(fft_vals)
# 创建 3D 坐标轴
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
# 绘制 3D 傅里叶变换结果
ax.bar(freqs, amps, zs=phases, zdir='y')
ax.set_xlabel('Frequency (Hz)')
ax.set_ylabel('Phase')
ax.set_zlabel('Amplitude')
# 显示图形
plt.show()
稍微解释一下,使用 np.linspace 生成一个包含1000 个点的时间序列 t,从 0 到 1000,然后根据这个时间序列生成一个带有多个频率分量的正弦波信号 y,其中包括频率为 10 Hz、30 Hz 和 60 Hz 的三个正弦波分量。这个是准备了一个测试数据。
接着,使用 np.fft.fftfreq 函数计算离散傅里叶变换中的频率值,也就是求出了10,30,60Hz,储存在变量freqs中,而后使用 np.fft.fft 函数对信号 y 进行傅里叶变换得到频域上的振幅和相位信息fft_vals, 分别通过求模和求角的方式计算出真正的振幅和相位。
剩下的就是matplotlib绘制三维图片,最终得到的图像已经在上文展示。这个三维图就是频域。
傅里叶变换:
了解完傅里叶级数,我们就可以了解傅里叶变换了。那么傅里叶变换有两种,第一种是离散型傅里叶变换,第二种是连续性傅里叶变换。
离散型傅里叶变换
对于离散型傅里叶变换,很简单,我们回到之前的傅里叶级数的公式:
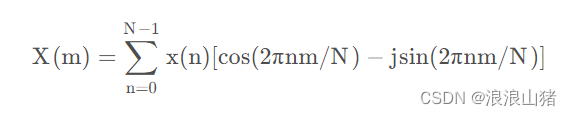
我们要了解一个公式叫做欧拉公式:

那么通过欧拉公式我们就能将傅里叶级数的原始公式转换成以指数形式表达的形式:
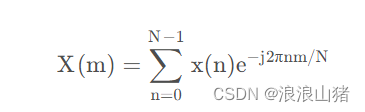
这个公式也就是我们常说的离散型傅里叶变换(Discrete Fourier Transform, DFT),其实就是傅里叶级数的指数型表达。
离散型傅里叶变换就是将连续时域信号转换为离散的频域信号的数学算法。例子在上文讲傅里叶级数的时候看到了,它的分解的结果是有限个。
连续性傅里叶变换
其实傅里叶变换的全名就叫连续性傅里叶变换,毕竟那些很有规律可以被分解成有限个波的的波在生活中也是少数。通常情况下,我们遇到的波都是没有规律的。
对于一个函数,他是没有周期的,那我们可以把他看作是一个周期为无穷的函数。
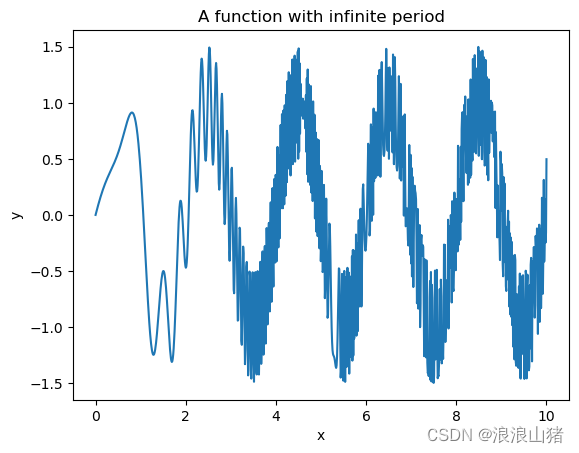
我们对这个函数做一个积分,

让原函数乘以e的-jωt次方,这个代表乘以其对应的一个正交积组合(理解不了这个也没关系)。然后做一个积分。这个积分就是连续性傅里叶变换。
这个积分有两种结果。如果它等于0,那么就没有ω,如果不等于0,那么他就有无数个ω。ω指组成这个波的其中一个波的ω。
写的正式一些
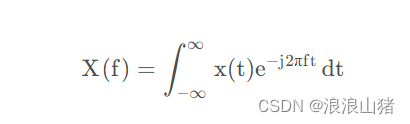
这就是连续性傅里叶变换的公式。
连续傅里叶变换(CTFT)和离散型傅里叶变换(DFT)不同,CTFT 的结果是一个连续的函数,在频域上对应于所有可能的频率,因此其结果是无限个。
后话
记住公式就行。后续我会在OpenCV系列博客中实际应用傅里叶变换。