VAE--part1

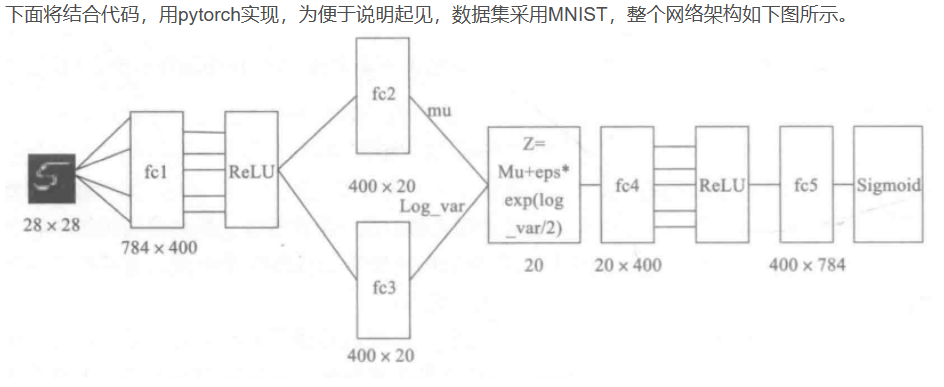
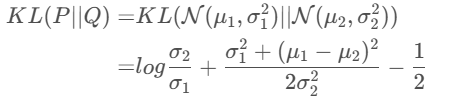参考博客仅做学习记录，侵删

分布变换

VAE和GAN都是生成式模型，它们俩的目标基本一致：希望构建一个从隐变量Z，来生成目标数据X的模型，但实现上有所不同。

更准确地讲，它们是假设Z服从了某些常见的分布(比如：正态分布或均匀分布)，然后希望训练一个模型X=g(Z), g为生成器generator, 这个模型可以将原来的概率分布映射到训练集的概率分布，即，它们的目的都是进行分布之间的变换。

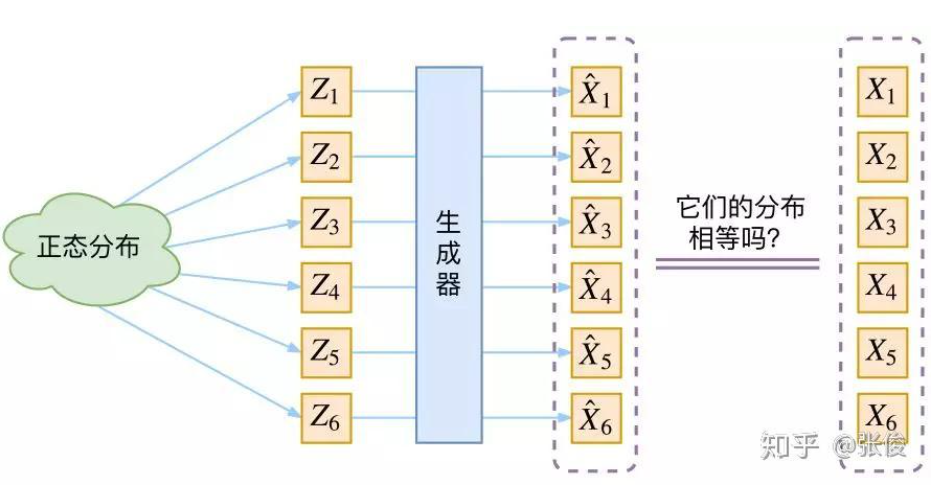
生成模型的难题就是判断生成分布与真实分布的相似度，因为我们只知道两者的采样结果，不知道它们的分布表达式。

那现在假设 Z 服从标准的正态分布，那我们就可以从中采样得到若干个 $Z_1,Z_2,Z_3,\cdots ,Z_n$, 然后输入到生成器中，得到${\hat{X}}_1=g(Z_1),{\hat{X}}_2=g(Z_2),\cdots {\hat{X}}_n=g(Z_n)$, 我们怎么判断这个通过 $g$ 构造出来的数据集，它的分布跟我们目标的数据集分布是不是一样的呢？

思考：
Q1：KL散度用来衡量两个分布之间的相似度，用KL散度可以吗？
答：不行，因为 KL 散度是根据两个概率分布的表达式来算它们的相似度的，然而目前我们并不知道它们的概率分布的表达式。

我们只有一批从构造的分布采样而来的数据{ ${\hat{X}}_1,{\hat{X}}_2,{\hat{X}}_3,\cdots ,{\hat{X}}_n$}, 还有一批从真实的分布采样而来的数据{ $X_1,X_2,X_3,\cdots ,X_n$}, 即训练集，我们只有样本本身，没有分布表达式，当然也就没有办法算 KL 散度。

虽然遇到困难，但还是要想办法解决的。GAN 的思路很直接粗犷：既然没有合适的度量，那我干脆把这个度量也用神经网络训练出来吧。

VAE慢谈

首先我们有一批数据样本{ $X_1,X_2,\cdots ,X_n$}，其整体用 X 来描述，我们本想根据{ $X_1,X_2,\cdots ,X_n$}得到 X 的分布 p(X), 如果能得到的话，那我直接根据 p(X) 来采样，这样就可以得到所有的 X 了(包括{ $X_1,X_2,\cdots ,X_n$}之外的 $X_i$), 这是一个终极理想的生成模型了。

当然，这个理想很难实现，于是我们将分布改一改：
$$p(X)=\sum _{Z}p(X|Z)p(Z)①$$

这里我们就不区分求和还是求积分了，意思对了就行。此时 p(X|Z) 就描述了一个由 Z 来生成 X的模型，而我们假设 Z 服从标准正态分布，也就是 $p(Z)=N(0,I)$。如果这个理想能实现，那么我们就可以先从标准正态分布中采样一个 Z，然后根据 Z 来算一个 X，也是一个很棒的生成模型。

接下来就是结合自编码器来实现重构，保证有效信息没有丢失，再加上一系列的推导，最后把模型实现。框架的示意图如下:

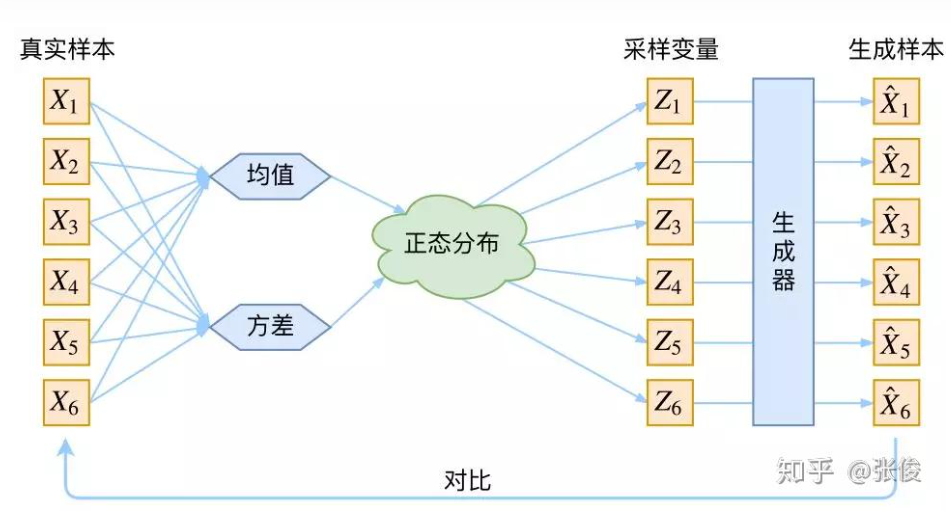
上图的疑惑所在：

对于上图的话，我们其实完全不清楚：究竟经过重新采样出来的$Z_k$，是不是还对应着原来的 $X_k$，所以我们如果直接最小化 $D({\hat{X}}_k,X_k{)}^2$（这里 D 代表某种距离函数）是很不科学的，而事实上你看代码也会发现根本不是这样实现的。

VAE 初现

其实，在整个 VAE 模型中，我们并没有去使用 p(Z)（先验分布）是正态分布的假设，我们用的是假设 p(Z|X)（后验分布）是正态分布。

具体来说，给定一个真实样本 $X_k$，我们假设存在一个专属于 $X_k$ 的分布 $p(Z|X_k)$（学名叫后验分布），并进一步假设分布 $p(Z|X_k)$ 是(独立的、多元的)正态分布。

为什么要强调“专属”呢？因为我们后面要训练一个生成器 X=g(Z)，希望能够把从分布 $p(Z|X_k)$ 采样出来的一个 $Z_k$ 还原为 $X_k$。

如果假设 p(Z) 是正态分布，然后从 p(Z) 中采样一个 Z，那么我们怎么知道这个 Z 对应于哪个真实的 X 呢？现在 $p(Z|X_k)$ 专属于 $X_k$，我们有理由说从这个分布采样出来的 Z 应该要还原到 $X_k$ 中去。

事实上，在论文 Auto-Encoding Variational Bayes 的应用部分，也特别强调了这一点：

In this case, we can let the variational approximate posterior be a multivariate Gaussian with a diagonal covariance structure:
$$\log q_{\varphi }(z|x_i)=\log N(z;{\mu }_i,{\sigma }_i^{2}I)②$$
论文中的上式是实现整个模型的关键，不知道为什么很多教程在介绍 VAE 时都没有把它凸显出来。尽管论文也提到 p(Z) 是标准正态分布，然而那其实并不是本质重要的。

再次强调，这时候每一个 $X_k$ 都配上了一个专属的正态分布，才方便后面的生成器做还原。但这样有多少个 X 就有多少个正态分布了。我们知道正态分布有两组参数：均值 $\mu$ 和方差 ${\sigma }^2$（如果X为向量的话，则$\mu$ 和${\sigma }^2$都是向量）。

那怎么找出专属于 $X_k$ 的正态分布 $p(Z|X_k)$ 的均值和方差呢？好像并没有什么直接的思路。

好吧，就用神经网络来拟合出来。这就是神经网络时代的哲学：难算的我们都用神经网络来拟合，在 WGAN 那里我们已经体验过一次了，现在再次体验到了。

于是我们构建了两个神经网络 ${\mu }_k=f_1(X_k),\log {\sigma }^2=f_2(X_k)$来求 $\mu$ 和 $\sigma$。我们选择拟合 $\log {\sigma }^2$, 而不是直接拟合 ${\sigma }^2$, 是因为 ${\sigma }^2$ 总是非负的，需要加激活函数处理，而拟合 $\log {\sigma }^2$ 不需要加激活函数，因为它可正可负。

具体这个是咋用神经网络去求$\mu ,\sigma$呢？可以参看下图
或者可以去看这篇博客：用VAE生成图像会得到更深刻的理解

到这里，我能知道专属于 $X_k$ 的均值和方差了，也就知道它的正态分布长什么样了，然后从这个专属分布中采样一个 $Z_k$ 出来，然后经过一个生成器得到 ${\hat{X}}_k=g(Z_k)$。
其实就是：
$$Z_k=\mu +ϵ\ast \sigma ,ϵ\sim N(0,1)③$$
也可以写成：$Z_k=\mu +ϵ\ast e^{\frac{1}{2}.\log {\sigma }^2},ϵ\sim N(0,1)④$，这俩式子本质都是一样的。

现在我们可以放心地最小化 $D({\hat{X}}_k,X_k{)}^2$，因为 $Z_k$ 是从专属 $X_k$ 的分布中采样出来的，这个生成器应该要把开始的 $X_k$ 还原回来。于是可以画出 VAE 的示意图：

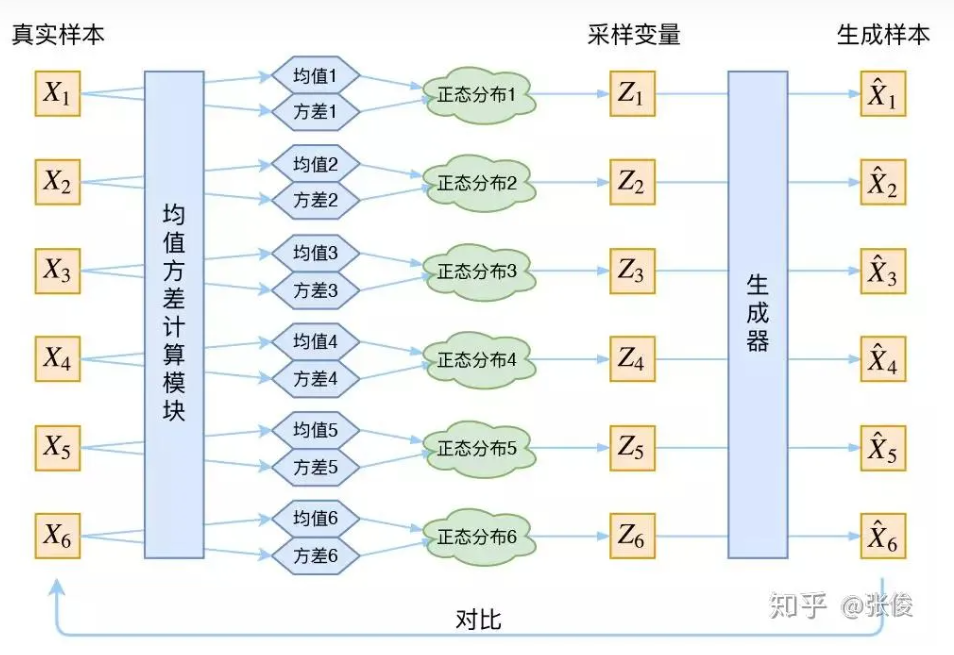
事实上，VAE 是为每个样本构造专属的正态分布，然后采样来重构。

分布标准化

让我们来思考一下，根据上图的训练过程，最终会得到什么结果。

首先，我们希望重构 X，也就是最小化 $D({\hat{X}}_k,X_k{)}^2$，但是这个重构过程受到噪声的影响，因为 $Z_k$ 是通过重新采样过的，即上面式子③$Z_k=\mu +ϵ\ast \sigma ,ϵ\sim N(0,1)$，不是直接由 encoder 算出来的,直接由encoder算出来的是$\mu ,\sigma$（或者$\log {\sigma }^2$）。

显然噪声会增加重构的难度，不过好在这个噪声强度（也就是方差$\sigma$）通过一个神经网络算出来的，所以最终模型为了重构得更好，肯定会想尽办法让方差为0。即让这个Z 更接近 X。

但是由$Z_k=\mu +ϵ\ast \sigma ,ϵ\sim N(0,1)$可知，当$\sigma =0$时，也就没有随机性了，即固定有$Z=\mu$，所以不管怎样采样其实都只是得到确定的结果(也就是均值$\mu$)，只拟合一个当然比拟合多个要容易，而均值是通过另外一个神经网络算出来的。

说白了，模型会慢慢退化为普通的AE(autoEncoder)，噪声不再起作用。

但是自编码器AE不能随意产生合理的潜在变量，从而导致它无法产生新的内容。因为潜在变量Z都是编码器从原始图片中产生的。这样不就白费力气了吗？说好的生成模型呢？

别急别急，其实 VAE 还让所有的 p(Z|X) 都向标准正态分布看齐，这样就防止了噪声为零，同时保证了模型具有生成能力。即不能都是$Z=\mu$,

那为什么这样就可以保证“生成能力”了呢？ 如果所有的 p(Z|X) 都很接近标准正态分布 N(0,I)，那么根据定义：
$$p(Z)=\sum _{X}p(Z|X)p(X)=\sum _{X}N(0,I)p(X)=N(0,I)\sum _{X}p(X)=N(0,I)⑤$$

这样我们就能达到我们的先验假设：p(Z) 是标准正态分布。然后我们就可以放心地从 N(0,I) 中采样来生成图像了。

为什么符合先验假设p(Z)是标准正态分布，就可以放心从N(0,I)中采样生成图像了呢？
答：个人理解是：如下图中的{ $Z_1,Z_2\cdots ,Z_6$}都是从N(0,I)中采样得到的，然后通过生成器可以得到{ $\widehat{X_1},\widehat{X_2},\cdots \widehat{X_6}$}（假设已经经过训练好了），那就是说训练后我们认为训练的还不错，即$\widehat{X_i}\approx X_i$,即生成样本和真实样本很像，即符合真实样本的分布。这个时候拿训练好的模型，然后从标准正态分布N(0,I)中随机采样Z，然后inference得到生成的样本也就可以认为是符合真实样本的分布了。

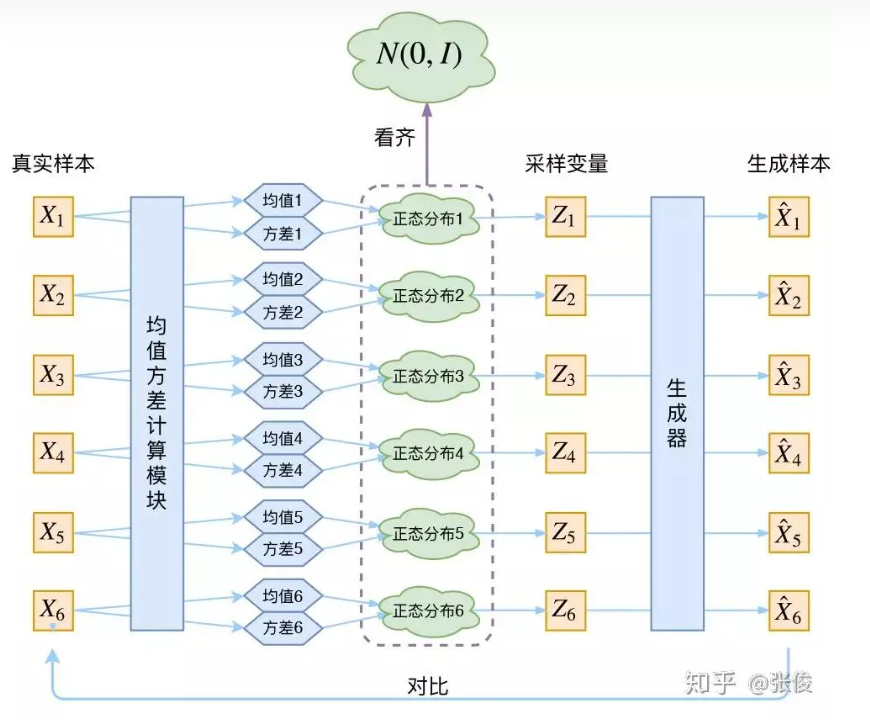
为了使模型具有生成能力，VAE要求每个p(Z|X)都向正态分布看齐。

那怎么让所有的 p(Z|X) 都向 N(0,I) 看齐呢？如果没有外部知识的话，其实最直接的方法应该是在重构误差的基础上中加入额外的 loss：

$${\mathcal{L}}_{\mu }={\Vert f_1\left(X_k\right)\Vert }^2⑥$$
$${\mathcal{L}}_{{\sigma }^2}={\Vert f_2\left(X_k\right)\Vert }^2⑦$$

因为它们分别代表了均值${\mu }_k$和方差的对数$\log {\sigma }^2$， 达到N(0,I)就是希望${\mathcal{L}}_{\mu }$和${\mathcal{L}}_{{\sigma }^2}$尽量接近于0。不过，这又会面临着这两个损失的比例要怎么选取的问题，选取得不好，生成的图像会比较模糊。

说明：
1.希望${\mathcal{L}}_{\mu }$尽量接近于0
首先要知道$f_1(X_k)$就是指：用神经网络求出来的$\mu$，那自然是希望$\mu$越接近0了。
2.为啥希望${\mathcal{L}}_{{\sigma }^2}$也尽量接近于0呢？
$f_1(X_k)$就是指：用神经网络求出来的$\log {\sigma }^2$。
因为是希望$\sigma \approx 1$, 那就是$\log {\sigma }^2\approx 0$。

所以，原论文直接算了一般（各分量独立的）正态分布与标准正态分布的 KL 散度 $KL(N(\mu ,{\sigma }^2)\Vert N(0,I))$ 作为这个额外的 loss，计算结果为：

$${\mathcal{L}}_{\mu ,{\sigma }^2}=\frac{1}{2}\sum _{i=1}^d({\mu }_{(i)}^2+{\sigma }_{(i)}^2-\log {\sigma }_i^2-1)⑧$$

这里的 d 是隐变量 Z 的维度，而 ${\mu }_{(i)}$ 和 ${\sigma }_{(i)}^2$ 分别代表一般正态分布的均值向量和方差向量的第 i 个分量。直接用这个式子做补充 loss，就不用考虑均值损失和方差损失的相对比例问题了。

显然，这个loss也可以分为两部分理解：
$${\mathcal{L}}_{\mu ,{\sigma }^2}={\mathcal{L}}_{\mu }+{\mathcal{L}}_{{\sigma }^2}⑨$$
$${\mathcal{L}}_{\mu }=\frac{1}{2}\sum _{i=1}^d{\mu }_{(i)}^2=\frac{1}{2}{\Vert f_1\left(X\right)\Vert }^2⑩$$
$${\mathcal{L}}_{{\sigma }^2}=\frac{1}{2}\sum _{i=1}^d({\sigma }_{(i)}^2-\log {\sigma }_{(i)}^2-1)$$

说明：
式⑧的由来：

具体可以见高斯分布的KL散度了解详细推导过程

重参数技巧

Reparameterization Trick

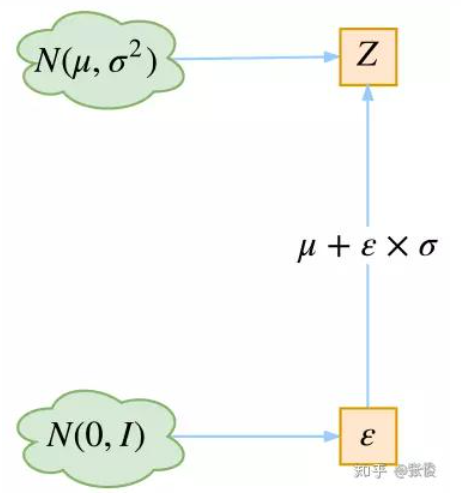
其实很简单，就是我们要从 $p(Z|X_k)$ 中采样一个 $Z_k$ 出来，尽管我们知道了 $p(Z|X_k)$ 是正态分布，但是均值方差都是靠模型算出来的，我们要靠这个过程反过来优化均值方差的模型，但是“采样”这个操作是不可导的，而采样的结果是可导的，于是我们利用了一个事实：

从$N(\mu ,{\sigma }^2)$中采样一个Z, 相当于从$N(0,I)$中采样一个$ϵ$, 然后让$Z=\mu +ϵ\ast \sigma$

所以，我们将从 $N(\mu ,{\sigma }^2)$
采样变成了从 $N(0,I)$
中采样，然后通过参数变换得到从$N(\mu ,{\sigma }^2)$ 中采样的结果。这样一来，“采样”这个操作就不用参与梯度下降了，改为采样的结果参与，使得整个模型可训练了。
具体可以参看这篇博客

VAE的本质是什么？

VAE 的本质是什么？VAE 虽然也称是 AE（AutoEncoder）的一种，但它的做法（或者说它对网络的诠释）是别具一格的。

在 VAE 中，它的 Encoder 有两个，一个用来计算均值，一个用来计算方差，这已经让人意外了：Encoder 不是用来 Encode 的，是用来算均值和方差的，这真是大新闻了，还有均值和方差不都是统计量吗，怎么是用神经网络来算的？

VAE 从让普通人望而生畏的变分和贝叶斯理论出发，最后落地到一个具体的模型中，虽然走了比较长的一段路，但最终的模型其实是很接地气的。

它本质上就是在我们常规的自编码器的基础上，对 encoder 的结果（在VAE中对应着计算均值的网络）加上了“高斯噪声”，使得结果 decoder 能够对噪声有鲁棒性；而那个额外的 KL loss（目的是让均值为 0，方差为 1），事实上就是相当于对 encoder 的一个正则项，希望 encoder 出来的东西均有零均值。

那另外一个 encoder（对应着计算方差$\sigma$的网络）的作用呢？它是用来动态调节噪声的强度的。

直觉上来想，当 decoder 还没有训练好时（重构误差远大于 KL loss），就会适当降低噪声（KL loss 增加），使得拟合起来容易一些（重构误差开始下降）。

反之，如果 decoder 训练得还不错时（重构误差小于 KL loss），这时候噪声就会增加（KL loss 减少），使得拟合更加困难了（重构误差又开始增加），这时候 decoder 就要想办法提高它的生成能力了。

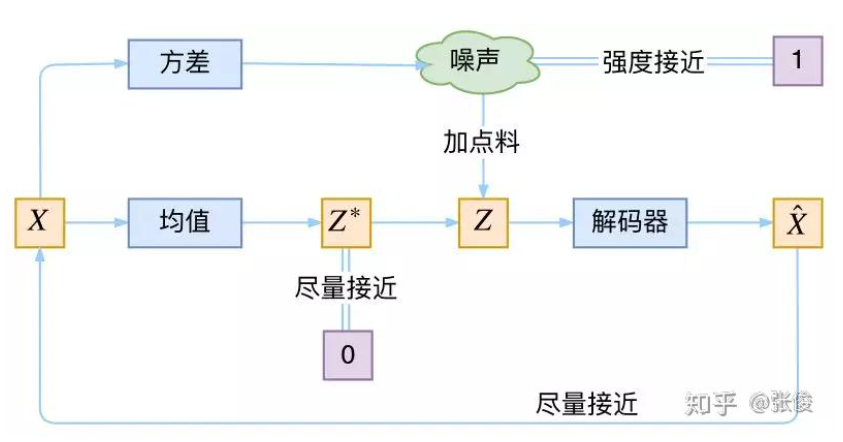
VAE的本质结构

说白了，重构的过程是希望没噪声的，而 KL loss 则希望有高斯噪声的，两者是对立的。所以，VAE 跟 GAN 一样，内部其实是包含了一个对抗的过程，只不过它们两者是混合起来，共同进化的。

说明：
重构：即训练的过程中，从$X_a$到Z再到$X_b$，自然是希望Z能稳定下来为一个定值，这样恢复出来的$X_b$就更具有确定性，更能接近真实样本$X_a$。

KL loss: 因为我们训练的目的就是为了让模型有生成能力，即从噪声出发，通过模型来生成符合真是样本分布的新样本。如果我们在训练过程中让Z稳定下来为一个定值，那我们在inference的时候就不能从噪声出发了。
因为我们最终的目的是：拿训练好的模型，然后从标准正态分布N(0,I)中随机采样Z，然后inference得到生成的样本也就可以认为是符合真实样本的分布了，所以我们并不能真的让Z为一个定值固定下来。这样用含有噪声的Z去生成$\widehat{X_i}$, 然后来衡量生成数据$\widehat{X_i}的分布$与原始数据$X_i$的分布之间的相似度，自然是越相似越好。

可以结合前面这个问题：**为什么符合先验假设p(Z)是标准正态分布，就可以放心从N(0,I)中采样生成图像了呢？**来进行思考。

正态分布？

对于 p(Z|X) 的分布，读者可能会有疑惑：是不是必须选择正态分布？可以选择均匀分布吗？

首先，这个本身是一个实验问题，两种分布都试一下就知道了。但是从直觉上来讲，正态分布要比均匀分布更加合理，因为正态分布有两组独立的参数：均值和方差，而均匀分布只有一组。

前面我们说，在 VAE 中，重构跟噪声是相互对抗的，重构误差跟噪声强度是两个相互对抗的指标，而在改变噪声强度时原则上需要有保持均值不变的能力，不然我们很难确定重构误差增大了，究竟是均值变化了（encoder的锅）还是方差变大了（噪声的锅）。

而均匀分布不能做到保持均值不变的情况下改变方差，所以正态分布应该更加合理。

变分在哪里

还有一个有意思（但不大重要）的问题是：VAE 叫做“变分自编码器”，它跟变分法有什么联系？在VAE 的论文和相关解读中，好像也没看到变分法的存在？

其实如果读者已经承认了 KL 散度的话，那 VAE 好像真的跟变分没多大关系了，因为 KL 散度的定义是：
$$KL(p(x)||q(x))=\int p(x)\ln \frac{p(x)}{q(x)}dx$$

如果是离散概率分布就要写成求和，我们要证明：已概率分布 p(x)（或固定q(x)）的情况下，对于任意的概率分布 q(x)（或 p(x)），都有 KL(p(x)‖q(x))≥0，而且只有当p(x)=q(x)时才等于零。
KL散度的非负性证明

因为 KL(p(x)‖q(x))实际上是一个泛函，要对泛函求极值就要用到变分法，当然，这里的变分法只是普通微积分的平行推广，还没涉及到真正复杂的变分法。而 VAE 的变分下界，是直接基于 KL 散度就得到的。所以直接承认了 KL 散度的话，就没有变分的什么事了。

一句话，VAE 的名字中“变分”，是因为它的推导过程用到了 KL 散度及其性质。