森林就是多棵树的集合,但是森林也可以只有一棵树,二叉树是一种特殊的树,固定的度为2,这是基本前情提要~
树常见的存储方式有三种:
(1)双亲表示法
仅用定义一个结点对象,一个数组,代码定义如下:
typedef struct {
char data;
int parent;
} Node;
typedef struct {
Node node[100];
int maxSize;
} NodeTree;
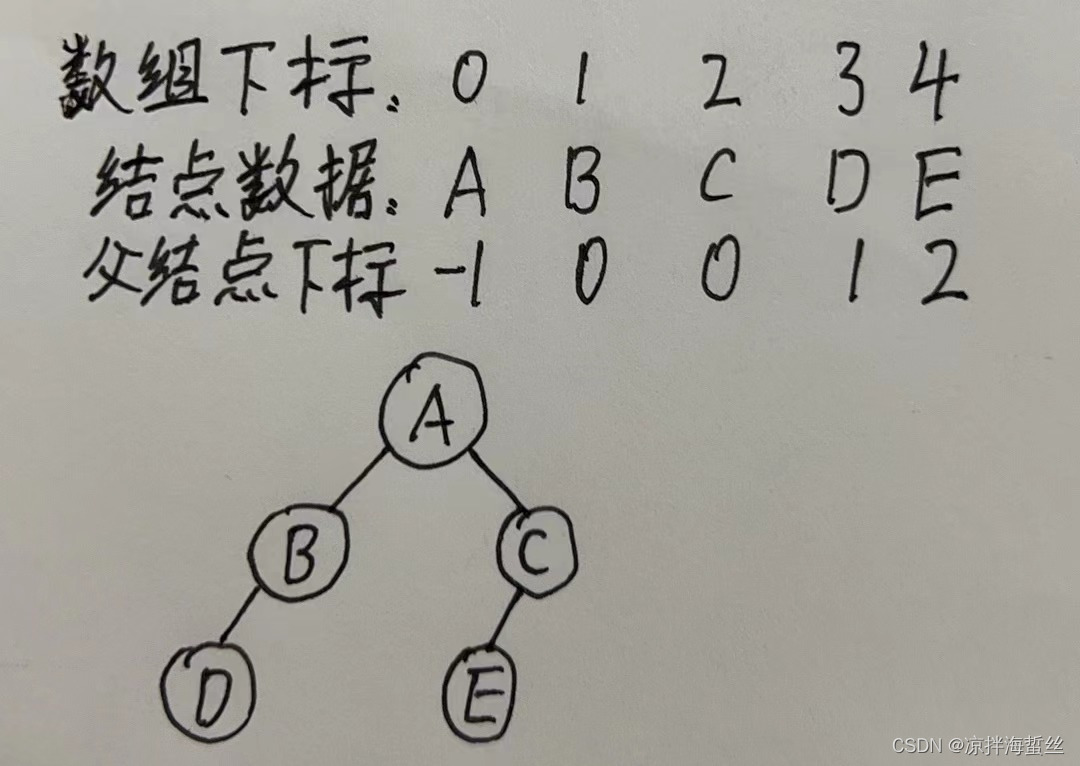
优点:由于对应元素的parent参数存储了父结点在数组中的下标,所以定义某个子结点的父结点非常简单,所以是:找父亲简单
缺点:但是如果想知道某个父亲x有多少个孩子,就必须遍历整个数组,看看哪个元素的parent是x,所以:找儿子们困难
(2)孩子表示法
为了克服找孩子困难问题,那么很容易想到把每个结点的孩子存起来,还是看定义比较简单理解
typedef struct {
char data;
int childs[];
} Node;
typedef struct {
Node node[100];
int maxSize;
} NodeTree;
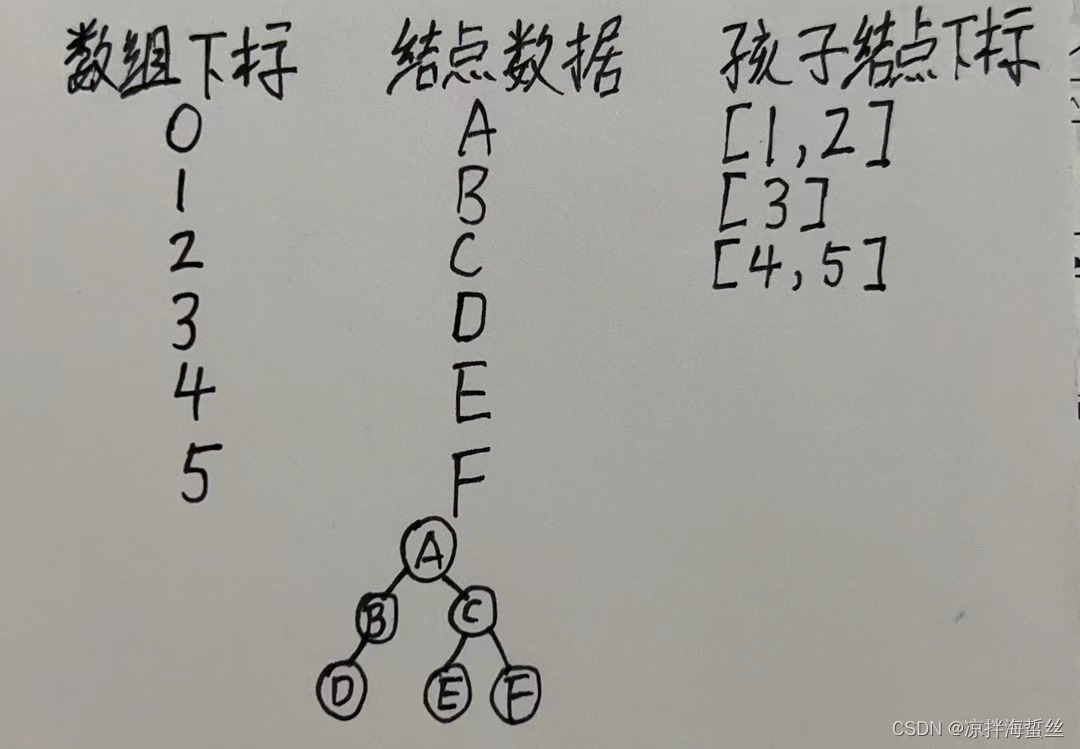
优点:找对应结点的孩子结点们简单
缺点:若要找某个结点的父结点,想象一下是不是应该拿着结点x的下标,去便利数组中所有的结点,看看x的下标在哪个结点的childs数组里面?
(注意,childs数组也可以用链表来实现,都一个意思)
记忆:双亲表示法找双亲简单,找孩子难;孩子表示法找孩子简单,找双亲难!
(3)孩子兄弟表示法
这个存储方式是最常用的,最方便的,而且它能很顺利实现树和二叉树甚至森林的转换,所以它很重要
结构定义上,它就是之前学过的双向链表而已,左指针指向孩子,右指针指向兄弟;也就是背到烂的“左孩子右兄弟”
typedef struct Nodes{
char data;
Nodes child;
Nodes sibling;
} Tree;
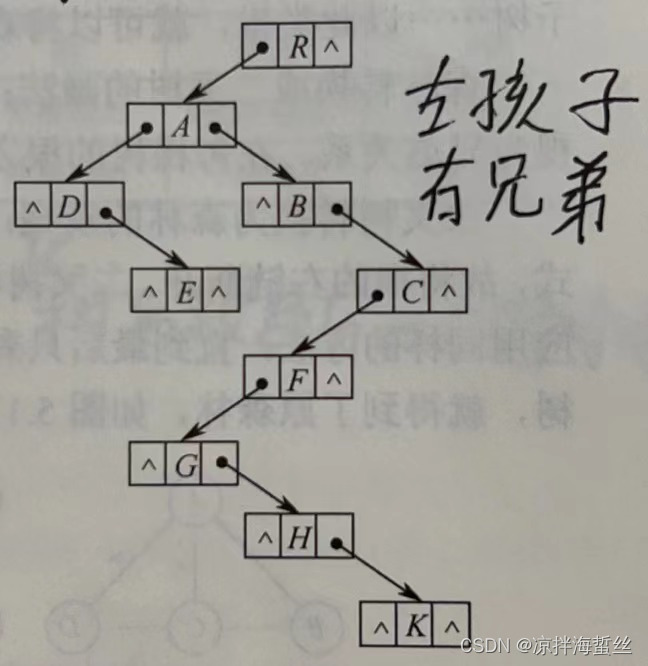
这种数据结构从父亲找孩子,或者从孩子找父亲都会很方便,例如如果需求需要根据孩子再找回父亲,只需要新增一个parent结点指回父亲结点即可(如果有父亲结点的指针,那么某个结点的右子树的parent应该全部一致,因为右兄弟,兄弟们的父亲肯定一样)
typedef struct Nodes{
char data;
Nodes parent;
Nodes child;
Nodes sibling;
} Tree;
树与二叉树的转换
规则还是“左孩子右兄弟”;不管有多少个兄弟,只要往右子树一直延伸即可,如下图:
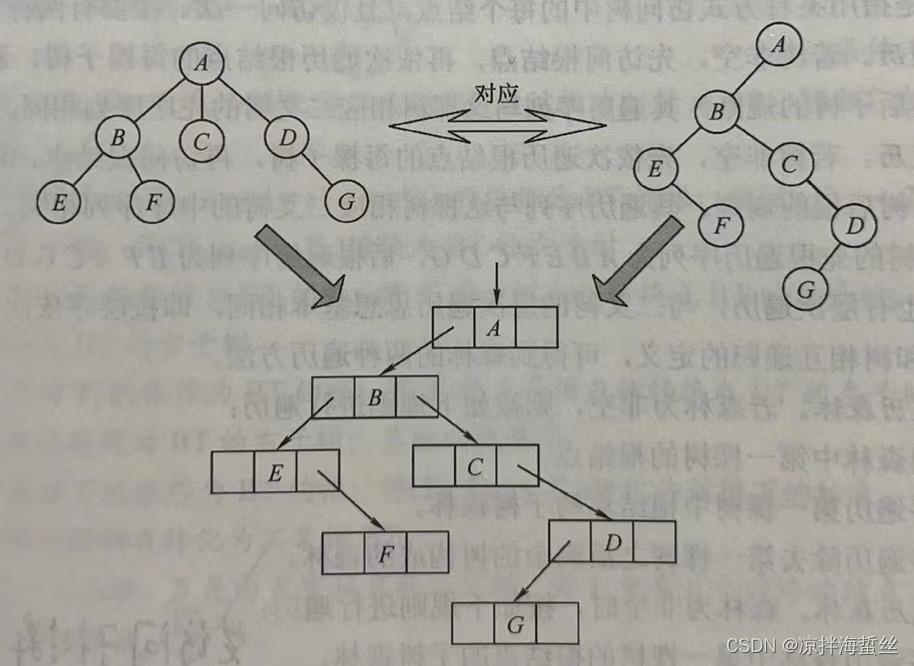
二叉树转换回树
因为根结点没有兄弟,所以它仅有左孩子,所以从二叉树的左结点入手,找左结点的全部右兄弟,使它们连接到左结点的parent结点(下图虚线所示),然后断开兄弟之间的连线(打叉叉的地方),然后再从第一个兄弟的左结点继续往下找,依次
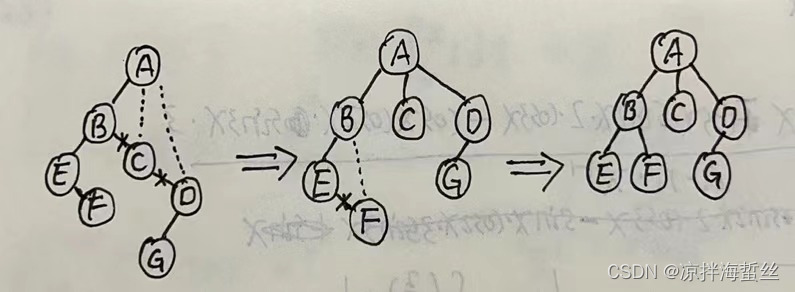
在这样转还回去的树中,可以发现,G结点放在D的左孩子位置可以,右孩子位置也可以;但是它们都是唯一的一棵树!
当时这个问题我纠结了一下,因为摆放左和右,不是对应不同样的两棵树吗?
后来回头看了资料,说是如果一个结点只有一个孩子,那么不管放在哪个位置,左还是右,都是同一棵树
但是有序树的两个孩子之间的位置就一定不能调换(例如EF的位置不能调换)。 如果是无序树,EF的位置就可以对换,还是同一棵无序树。
森林转换成二叉树
所谓森林,就是多棵树构成的,这非常好理解,
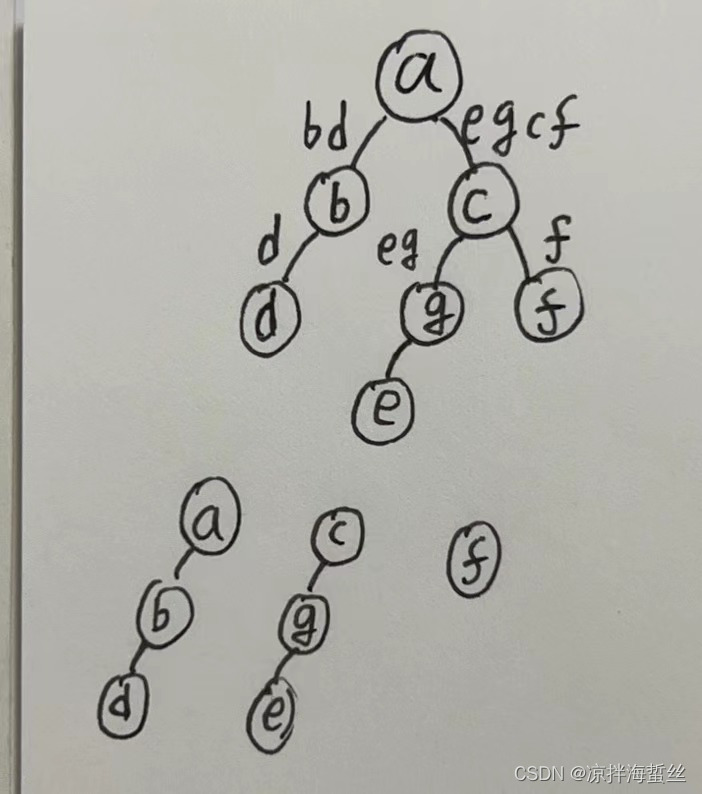
将森林转二叉树,首先运用左孩子右兄弟的规则,把每棵树都单独转成二叉树,然后再运用左孩子右兄弟的规则,把三棵同属于该森林的兄弟二叉树连起来即可,如下图:
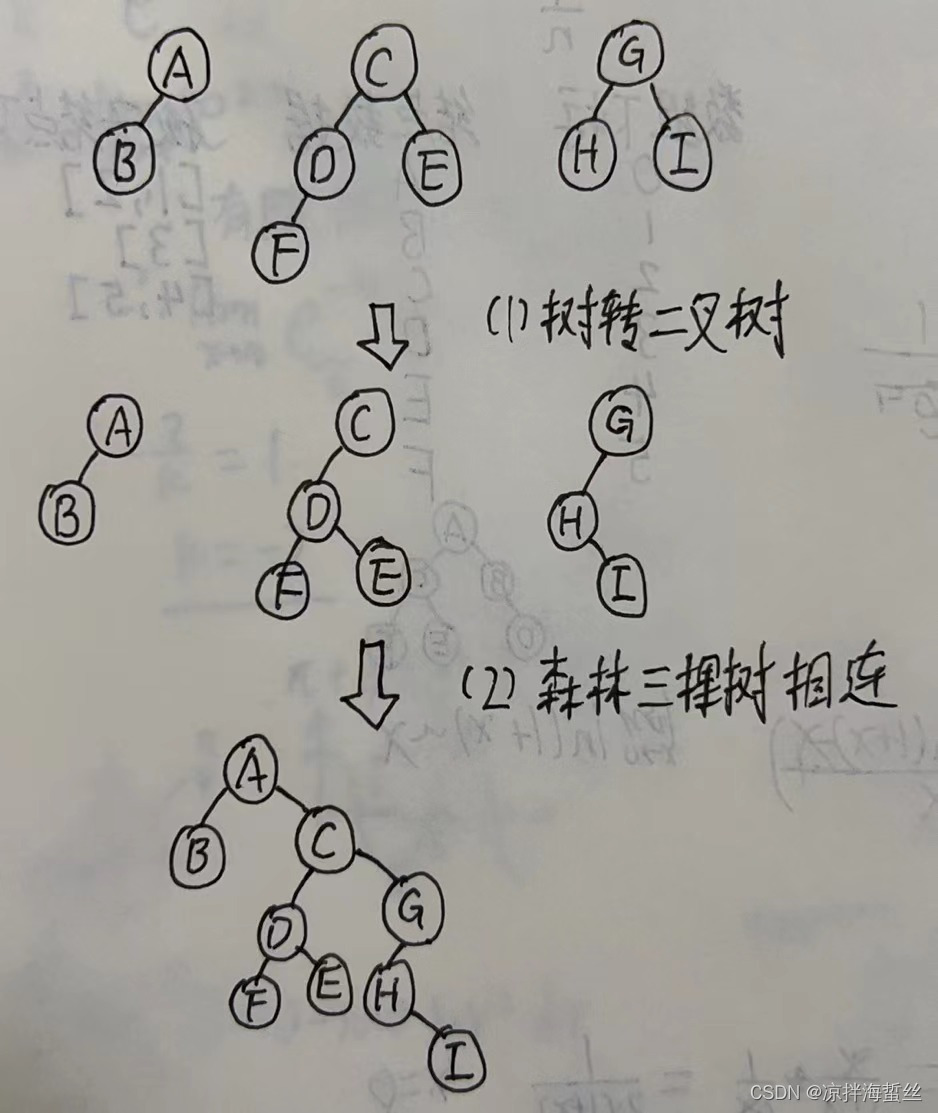
二叉树转换回森林
有了上图的例子,二叉树转回森林其实也非常好理解
(1)首先把根结点的右兄弟单独一个个断开联系,使其成为独立的二叉树
(2)根据二叉树转树的规则,左孩子右兄弟,恢复成原来的树即可
其实就是上图的逆操作过程,这里就不画新图了
遍历
二叉树的遍历:
先序遍历:根左右(NLR)
中序遍历:左根右(LNR)
后序遍历:左右根(LRN)
层次遍历:即从根结点开始,从上往下,从左往右依次扫描结点遍历
(若给出中序和其它任意一种遍历序,都可以还原回唯一的一棵二叉树)
树的遍历
由于树每个结点可能有多个孩子,所以它不可能规定哪个孩子在前的遍历顺序,只能规定父结点优先或者孩子们优先
先根遍历:先访问根结点,再依次遍历孩子结点(若孩子结点又是根结点,则深入下一层继续找孩子的孩子,这种专注于找孩子的遍历方式,很明显用孩子表示法比较简单实现)
后根遍历:从最左下角的孩子开始,先依次遍历各个孩子结点,最后访问根结点,逐层上升
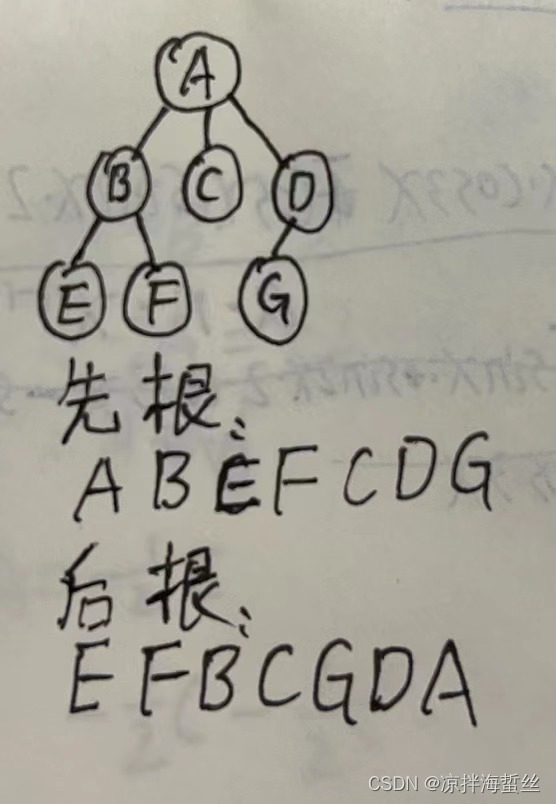
层次遍历:与二叉树层次遍历一样,从上至下从左到右,依次遍历每个结点
森林的遍历
先序遍历:
先遍历第一棵树的根结点
先序遍历第一棵树中根结点的子树森林
先序遍历第二棵树…
简单点说,就是一棵棵树用先序遍历即可
中序遍历(后序遍历):
记住这里有点坑!所谓森林的中序遍历!其实是先访问第一棵树的子树森林,最后才访问第一棵树的根结点
然后继续开始访问第二棵树的子树森林,最后访问第二棵树的根结点…
以此类推,直到一棵棵树访问完
其实,这就是最后才访问根结点,所以也称之为后序遍历
(森林所生成的对应的二叉树,其森林的中序遍历或者称后序遍历,一定一定一定跟对应的二叉树的中序遍历结果一样!)
这样说很抽象,还是看图:
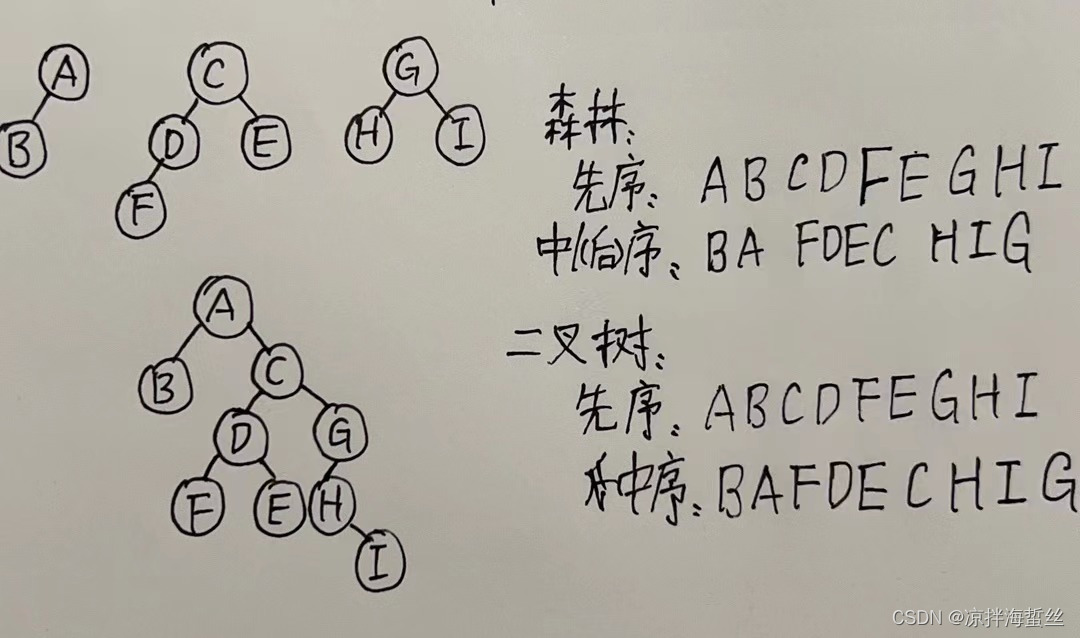
例子:
1 : 若T1是有序树T转换而来的二叉树,则T中结点的后根序列就是T1中结点的(中序)序列
因为T1是二叉树,T1是有序树(有序树则说明它的左右结点不能对换位置,是有序的,以此保证二叉树唯一),树的后根遍历,就是二叉树的中序遍历。
解析:
因为树转二叉树后,对应二叉树只有左子树(根结点无右兄弟,所以无右子树),对树做后根遍历,则是先把孩子们扫了一遍,最后扫父亲。而对于仅有左子树的二叉树来说,做中序遍历是:左中右,既然无右子树,其实也只是把左边全部孩子扫一遍,最后扫根结点父亲。那么这两者的顺序就是一样的了。
也可以画图看:
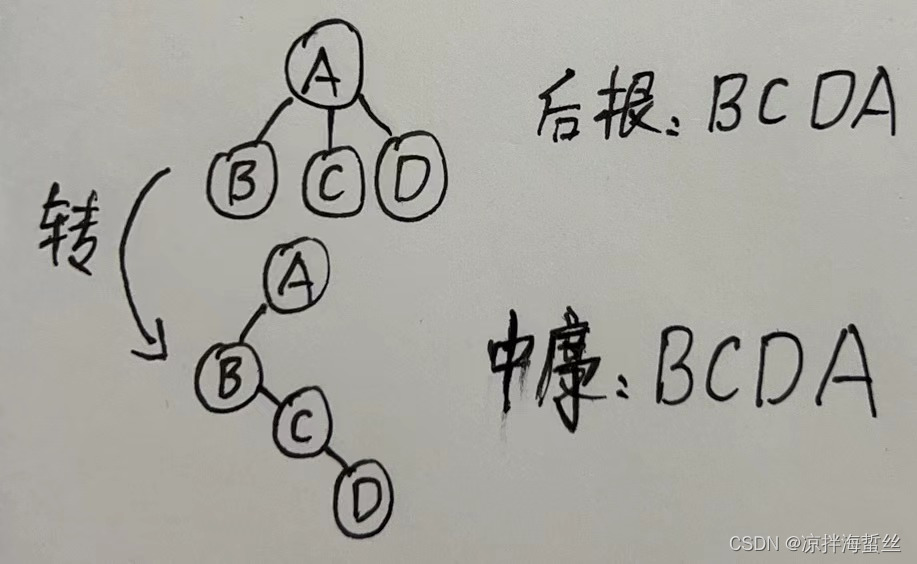
或者死记:树的后根遍历 = 二叉树的中序遍历
这个在2019年真题中也考到了
(2)设森林F有3棵树,第一第二第三棵树的结点个数分别为M1,M2,M3。与森林F对应的二叉树根结点的右子树上的结点个数是(M2+M3)
这题只需要回想一下上面我们自己推导的森林转成二叉树的过程,不难想象出对应二叉树的右子树其实就是其余两棵树的总结点数
(3)设森林F对应的二叉树为B,它有m个结点,B的根为p,p的右子树结点个数为n,森林F中第一棵树的结点个数是:m-n
森林总结点数为m,即二叉树的总结点数也是m, 根p的右子树结点数有n个,我们根据森林转二叉树规则知道根结点的右子树都是由森林中其它树构成的,既然右子树结点n,也就是除了第一棵树外总的结点数n,所以第一棵树就有m-n个结点
(4)设F是一个森林,B是由F变换来的二叉树,若F中有n个非终端结点,则B中右指针域为空的个数有()个
右指针域为空,也就是没有右兄弟,在森林变成二叉树过程,最后一棵树肯定没有右兄弟,所以它右指针域一定为空
⚠️其次,每一个非终端结点,也就是说肯定会有左孩子,在转换成二叉树后,最后那个孩子肯定没有右兄弟,所以n个非终端结点,会产生n个空的右指针域。
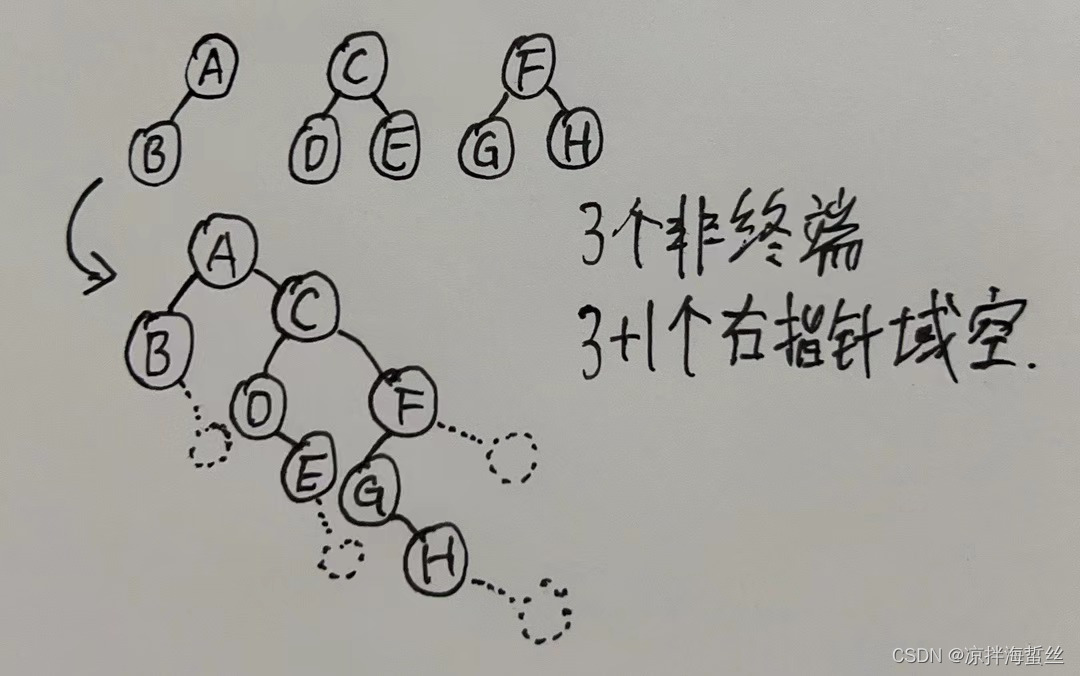
这种题还是画图,然后看题目中哪个选项符合比较好做。光靠想很难理解…
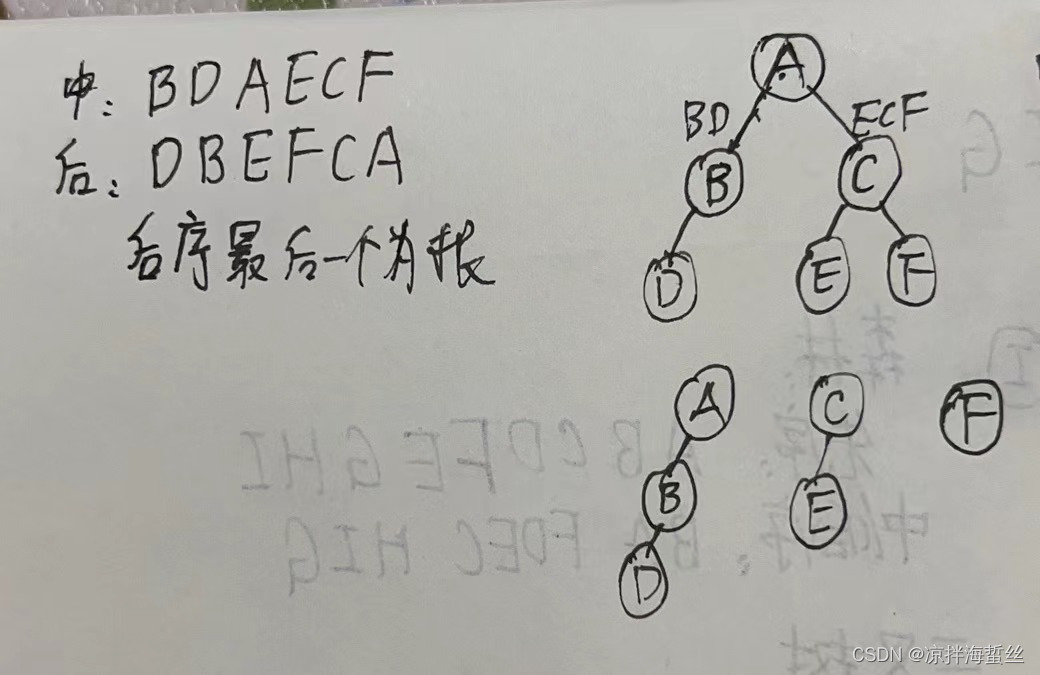
(5)某二叉树结点的中序序列为BDAECF, 后序序列为DBEFCA,则该二叉树对应的森林包括(3)棵树
首先要根据中序后序复原二叉树,首先抓后序最后一个是根,A
A在中序中的位置,把结点分成左子树BD和右子树ECF
再根据后序“左右中”,确定D肯定是左子树中最先被访问到的左结点,那么B只能是其父结点(B不可能是其右兄弟,因为这样的话他们就要有一个父结点,可是左子树只有他两,D又不父,只能B当父亲)
这样左子树就恢复完成了
右子树中,ECF,根据中序遍历左中右,很明显E是左孩子,C是父结点,F是右孩子
如果不放心,再根据后序看看:EFC,左右中,E还是左孩子,F右孩子,C是父结点
(6)【2009】将森林转换成对应的二叉树,若在二叉树中,结点U是结点V的父结点的父结点,则在原来森林中,U和V可能具有的关系是:
V和它的父结点若在U的右侧,则在原森林中它们是兄弟关系
V和它的父结点若在U的左侧,则在原森林中V和它的父是U的孩子和孙子关系
若在原森林中U还有父结点,则不管V和它的父结点在U的左侧还是右侧,辈分都是比U的父结点小
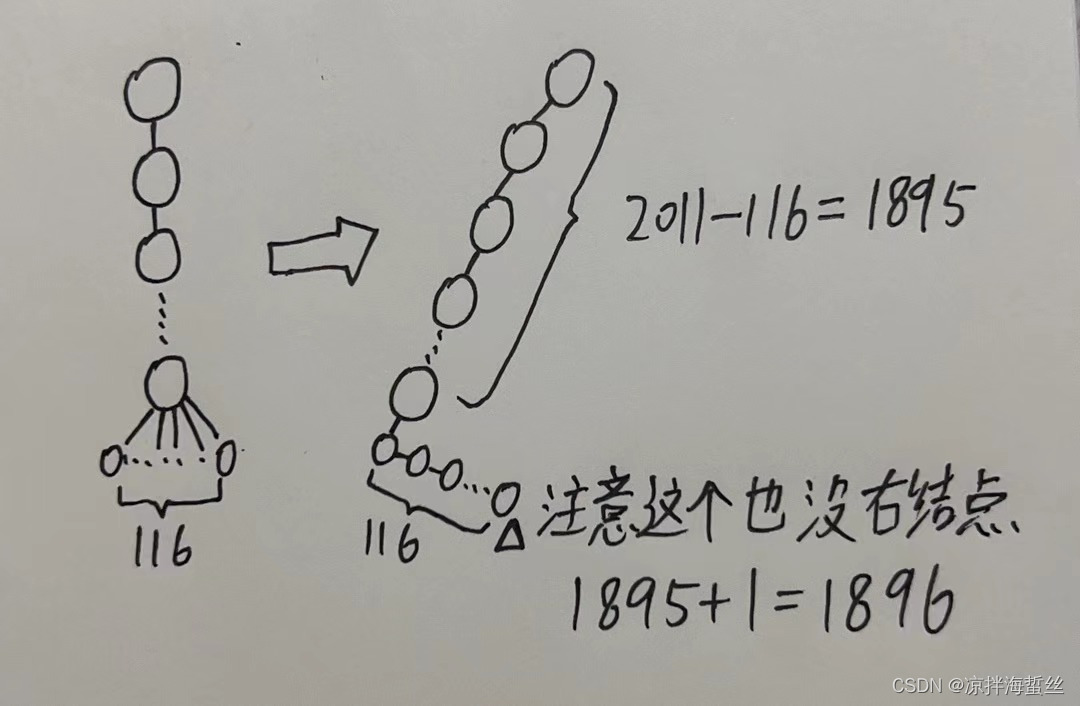
(7)【2011】已知一棵有2011个结点的树,其叶子结点个数为116,该树对应的二叉树中无右孩子的结点个数是:
(8)【2014】将森林F转换为对应的二叉树T,F中叶结点的个数等于(T中左孩子指针为空的结点个数)
因为T为对应二叉树,若T无左孩子,证明对应结点没有孩子(左孩子右兄弟),所以没有左孩子的一定是原森林F中的叶子结点
(6)【2020】已知森林F及与之对应的二叉树T,若F的先根遍历序列是a,b,c,d,e,f ,中根遍历是b,a,d,f,e,c ,则T的后根遍历序列是:
注意森林的中根遍历也是后根遍历,它是一棵棵树逐个遍历的,要注意跟二叉树的后序遍历区分
这个问题只给出了森林F的中根和先根,但是经过上面推导知道,森林的先根和中根遍历与对应的二叉树的先序和中序完全一致,所以直接按照森林的遍历顺序来恢复二叉树
先根的第一个a肯定是根结点
根结点a把中根切成两半,因为中根遍历是“左中右”,那么左边只有一个b, 且b肯定只能是a的左孩子,右边子树部分有d,f,e,c;
再根据先序“中左右”,第三个位置是c,则c是右子树的根结点,C在中根遍历中的位置又会把结点切分成左右子树,可看到dfe都是c的左孩子
再根据先序,第四个位置是d,则d是c的左子树的根结点,也就是c的左孩子,c在中根遍历中的位置再次把结点切分,看到fe是d的右孩子
…这个逻辑慢慢推,就能把二叉树还原出来,最后根据还原的二叉树,做一次后根遍历即可
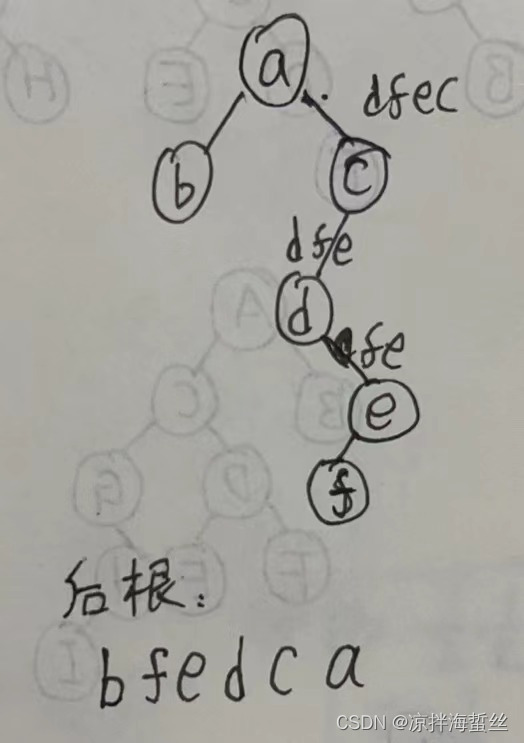
(7)【2021】某森林F对应的二叉树为T,若T的先序遍历序列是a,b,d,c,e,g,f 中序遍历是 b,d,a,e,g,c,f 则F中树的棵数是:3
还是按照T的遍历序列先还原,然后看根结点有多少个右孩子即可:
代码设计:
(1)编程求以孩子兄弟表示法存储的森林的叶子结点数
算法思路:
以孩子兄弟表示法的链式存储结构,则无左孩子的一定是叶子结点,我们仅需定义一个全局变量sum,然后对该森林生成的二叉树进行一次先序遍历,当某个结点没有左孩子,就sum++;直到遍历完成,得到的就是原森林中所有树的所有叶子结点数
伪代码如下:
int sum = 0;
findLeaves(Tree t){
if(t==null){
return ;
}
if(t.lchild == null){
sum ++;
}
findLeaves(t.lchild); // 递归找左子树
findLeaves(t.rchild); // 递归找右子树
}
(2)以孩子兄弟链表为存储结构,设计递归算法求树的深度
算法思路:
求深度,还是可以先序遍历,定义一个全局变量deep和max,每次递归下一层就deep++,判断++后的deep是否大于max最大深度,如果是,把deep赋值给max,记住递归结束的时候要deep–恢复上一层的深度数,不如deep只增不减。
伪代码如下:
int deep = 0;
int max = 0;
findDeep(Tree t, deep){
if(t==null){
return 0;
}
deep++;
if(deep > max){
max = deep;
}
findDeep(t.lchild, deep);
findDeep(t.rchild, deep);
deep--;
}
(3)已知一棵树的层次序列及每个结点的度,编写算法构造此数的孩子兄弟链表
算法思路:
树转二叉树,左孩子右兄弟,链表存储,第一层只有一个根结点只有左孩子,无右兄弟(右指针为空),第二层结点才可能开始有左孩子和右兄弟(即左右指针不为空)
已知层次序列数组和每个结点的度的数组,首先创建一个根结点T,定义类似双向链表的结构体,把层次序列的第一个元素A塞进根结点T中(根结点无兄弟),然后令它左结点是层次序列的第二个元素B
这个时候从结点度的数组中查找第1个元素A的度(即它会有多少个孩子),把度-1(减去B),for循环拼在B的右指针域链表(A的孩子就是B的兄弟,所以拼在右边);每拼一个,都从层次遍历数组中拿一个元素放入新的结点中,记住这里数组下标要随着变,模拟出队。
再从度的数组中找到B的度,循环给它生成左孩子,链接在左边
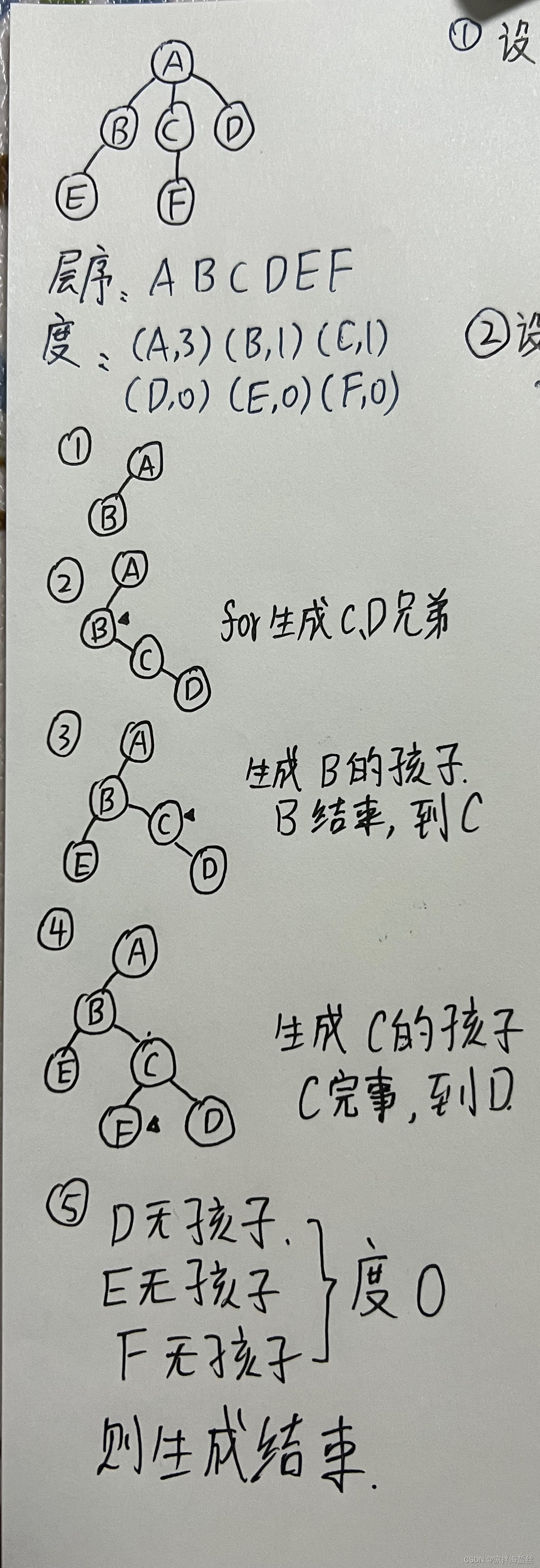
核心是针对层次遍历的数组做每个元素的循环,看看该元素的度多少(在原来树中的度,就代表了它有多少个孩子),还要注意上一层父结点的度数-1的值,下一层第一个孩子就要循环往自己右结点拼多少个兄弟。