Glow introduce

设$X$是一个真实但分布未知的高维随机向量，记为$X\sim p^{\ast }(X)$。我们收集了独立同分布的数据集$D$，我们选择带有参数$\theta$的模型$p_{\theta }(X)$，假设数据$X$是离散的，则log-likehood（log似然）的目的等效于最小化下面的公示：
$$L(D)=\frac{1}{N}\sum _{i=1}^N(-log{p}_{\theta }(X^{(i)}))$$

大多数的基于流的生成模型，其过程可以定义为：
$$z\sim p_{\theta }(z)$$
$$x=g_{\theta }(z)$$
$z$是潜在变量，$p_{\theta }(z)$是一个简单的概率密度，比如球形高斯：$p_{\theta }(z)=N(z;0,I)$

函数$g_{\theta }$是可逆的，也叫双射，给一个数据$x$，潜变量可以通过$z=f_{\theta }(x)=g_{\theta }^{-1}(x)$

为了简便，下面我们将省略下标$\theta$

我们假设函数$f$由一系列的转换组成：$f=f_1\circ f_2\circ \cdot \cdot \cdot \circ f_n$，如此$x$和$z$的关系可以描述为：

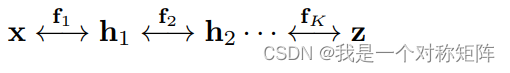
这样一个可逆变换的序列也可以被称为(正则化)流，