目录
- 第六章
-
- 17.设机器数字长为8位(含1位符号位),对下列各机器数进行算术左移一位、两位,算术右移一位、两位,讨论结果是否正确。
- 18.试比较逻辑移位和算术移位。
- 19.设机器数字长为8位(含1位符号位),用补码运算规则计算下列各题。
- 20.用原码一位乘、两位乘和补码一位乘(Booth算法)、两位乘计算x·y。
- 21.用原码加减交替法和补码加减交替法计算 x ÷ y x\div y x÷y。
- 22.设机器字长为16位(含1位符号位),若一次移位需 1 μ s 1\mu s 1μs,一次加法需 1 μ s 1\mu s 1μs,试问原码一位乘、补码一位乘、原码加减交替除和补码加减交替除法最多各需多少时间?
- 23.画出实现 Booth算法的运算器框图。
- 24.画出实现补码加减交替法的运算器框图。
- 25.对于尾数为40位的浮点数(不包括符号位在内),若采用不同的机器数表示,试问当尾数左规或右规时,最多移位次数各为多少?
- 26.按机器补码浮点运算步骤计算 [ x ± y ] 补 [x\pm y]_补 [x±y]补
- 27.假设阶码取3位,尾数取6位(均不包括符号位),计算下列各题。
- 28.如何判断定点和浮点补码加减运算结果是否溢出,如何判断原码和补码的定点除法运算结果是否溢出?
- 29.设浮点数阶码取3位,尾数取6位(均不包括符号位),要求阶码用移码运算,尾数用补码运算,计算x·y,且结果保留1倍字长。
- 30.机器数格式同上题,要求阶码用移码运算,尾数用补码运算,计算 x ÷ y x\div y x÷y。(注:改用阶移尾原格式作。)
- 31.设机器字长为32位,用与非门和与或非门设计一个并行加法器(假设与非门的延迟时间为30ns,与或非门的延迟时间为45ns),要求完成32位加法时间不得超过0.6 μ s \mu s μs。画出进位链及加法器逻辑框图。
- 32.设机器字长为16位,分别按4、4、4、4和5、5、3、3分组后
第六章
17.设机器数字长为8位(含1位符号位),对下列各机器数进行算术左移一位、两位,算术右移一位、两位,讨论结果是否正确。
[ x 1 ] 原 = 0.001 1010 ; [ y 1 ] 补 = 0.101 0100 ; [ z 1 ] 反 = 1.010 1111 ; [x1]_原=0.001\ 1010;[y1]_补=0.101\ 0100;[z1]_反=1.010\ 1111; [x1]原=0.001 1010;[y1]补=0.101 0100;[z1]反=1.010 1111;
[ x 2 ] 原 = 1.110 1000 ; [ y 2 ] 补 = 1.110 1000 ; [ z 2 ] 反 = 1.110 1000 ; [x2]_原=1.110\ 1000;[y2]_补=1.110\ 1000;[z2]_反=1.110\ 1000; [x2]原=1.110 1000;[y2]补=1.110 1000;[z2]反=1.110 1000;
[ x 3 ] 原 = 1.001 1001 ; [ y 3 ] 补 = 1.001 1001 ; [ z 3 ] 反 = 1.001 1001 。 [x3]_原=1.001\ 1001;[y3]_补=1.001\ 1001;[z3]_反=1.001\ 1001。 [x3]原=1.001 1001;[y3]补=1.001 1001;[z3]反=1.001 1001。
答:
算术左移一位:
[ x 1 ] 原 = 0.011 0100 ; 正确 [x_1]_原=0.011\ 0100;正确 [x1]原=0.011 0100;正确
[ x 2 ] 原 = 1.101 0000 ; 溢出 ( 丢 1 ) 出错 [x_2]_原=1.101\ 0000;溢出(丢1)出错 [x2]原=1.101 0000;溢出(丢1)出错
[ x 3 ] 原 = 1.011 0010 ; 正确 [x_3]_原=1.011\ 0010;正确 [x3]原=1.011 0010;正确
[ y 1 ] 补 = 0.010 1000 ; 溢出 ( 丢 1 ) 出错 [y_1]_补=0.010\ 1000;溢出(丢1)出错 [y1]补=0.010 1000;溢出(丢1)出错
[ y 2 ] 补 = 1.101 0000 ; 正确 [y_2]_补=1.101\ 0000;正确 [y2]补=1.101 0000;正确
[ y 3 ] 补 = 1.011 0010 ; 溢出 ( 丢 0 ) 出错 [y_3]_补=1.011\ 0010;溢出(丢0)出错 [y3]补=1.011 0010;溢出(丢0)出错
[ z 1 ] 反 = 1.101 1111 ; 溢出 ( 丢 0 ) 出错 [z_1]_反=1.101\ 1111;溢出(丢0)出错 [z1]反=1.101 1111;溢出(丢0)出错
[ z 2 ] 反 = 1.101 0001 ; 正确 [z_2]_反=1.101\ 0001;正确 [z2]反=1.101 0001;正确
[ z 3 ] 反 = 1.011 0011 ; 溢出 ( 丢 0 ) 出错 [z_3]_反=1.011\ 0011;溢出(丢0)出错 [z3]反=1.011 0011;溢出(丢0)出错
算术左移两位:
[ x 1 ] 原 = 0.110 1000 ; 正确 [x_1]_原=0.110\ 1000;正确 [x1]原=0.110 1000;正确
[ x 2 ] 原 = 1.010 0000 ; 溢出 ( 丢 11 ) 出错 [x_2]_原=1.010\ 0000;溢出(丢11)出错 [x2]原=1.010 0000;溢出(丢11)出错
[ x 3 ] 原 = 1.110 0100 ; 正确 [x_3]_原=1. 110\ 0100;正确 [x3]原=1.110 0100;正确
[ y 1 ] 补 = 0.101 0000 ; 溢出 ( 丢 10 ) 出错 [y_1]_补=0.101\ 0000;溢出(丢10)出错 [y1]补=0.101 0000;溢出(丢10)出错
[ y 2 ] 补 = 1.010 0000 ; 正确 [y_2]_补=1.010\ 0000;正确 [y2]补=1.010 0000;正确
[ y 3 ] 补 = 1.110 0100 ; 溢出 ( 丢 00 ) 出错 [y_3]_补=1.110\ 0100;溢出(丢00)出错 [y3]补=1.110 0100;溢出(丢00)出错
[ z 1 ] 反 = 1.011 1111 ; 溢出 ( 丢 01 ) 出错 [z_1]_反=1.011\ 1111;溢出(丢01)出错 [z1]反=1.011 1111;溢出(丢01)出错
[ z 2 ] 反 = 1.010 0011 ; 正确 [z_2]_反 =1.010\ 0011;正确 [z2]反=1.010 0011;正确
[ z 3 ] 反 = 1.110 0111 ; 溢出 ( 丢 00 ) 出错 [z_3]_反 =1.110\ 0111;溢出(丢00)出错 [z3]反=1.110 0111;溢出(丢00)出错
算术右移一位:
[ x 1 ] 原 = 0.000 1101 ; 正确 [x_1]_原=0.000\ 1101;正确 [x1]原=0.000 1101;正确
[ x 2 ] 原 = 1.011 0100 ; 正确 [x_2]_原=1.011\ 0100;正确 [x2]原=1.011 0100;正确
[ x 3 ] 原 = 1.000 1100 ( 1 ) ; 丢 1 ,产生误差 [x_3]_原=1.000\ 1100(1);丢1,产生误差 [x3]原=1.000 1100(1);丢1,产生误差
[ y 1 ] 补 = 0.010 1010 ; 正确 [y_1]_补=0.010\ 1010;正确 [y1]补=0.010 1010;正确
[ y 2 ] 补 = 1.111 0100 ; 正确 [y_2]_补=1.111\ 0100;正确 [y2]补=1.111 0100;正确
[ y 3 ] 补 = 1.100 1100 ( 1 ) ; 丢 1 ,产生误差 [y_3]_补=1.100\ 1100(1);丢1,产生误差 [y3]补=1.100 1100(1);丢1,产生误差
[ z 1 ] 反 = 1.101 0111 ; 正确 [z_1]_反=1.101\ 0111;正确 [z1]反=1.101 0111;正确
[ z 2 ] 反 = 1.111 0100 ( 0 ) ; 丢 0 ,产生误差 [z_2]_反=1.111\ 0100(0);丢0,产生误差 [z2]反=1.111 0100(0);丢0,产生误差
[ z 3 ] 反 = 1.100 1100 ; 正确 [z_3]_反=1.100\ 1100;正确 [z3]反=1.100 1100;正确
算术右移两位:
[ x 1 ] 原 = 0.000 0110 ( 10 ) ; 产生误差 [x_1]_原=0.000\ 0110(10);产生误差 [x1]原=0.000 0110(10);产生误差
[ x 2 ] 原 = 1.001 1010 ; 正确 [x_2]_原=1.001\ 1010;正确 [x2]原=1.001 1010;正确
[ x 3 ] 原 = 1.000 0110 ( 01 ) ; 产生误差 [x_3]_原=1.000\ 0110(01);产生误差 [x3]原=1.000 0110(01);产生误差
[ y 1 ] 补 = 0.001 0101 ; 正确 [y_1]_补=0.001\ 0101;正确 [y1]补=0.001 0101;正确
[ y 2 ] 补 = 1.111 1010 ; 正确 [y_2]_补=1.111\ 1010;正确 [y2]补=1.111 1010;正确
[ y 3 ] 补 = 1.110 0110 ( 01 ) ; 产生误差 [y_3]_补=1.110\ 0110(01);产生误差 [y3]补=1.110 0110(01);产生误差
[ z 1 ] 反 = 1.110 1011 ; 正确 [z_1]_反=1.110\ 1011;正确 [z1]反=1.110 1011;正确
[ z 2 ] 反 = 1.111 1010 ( 00 ) ; 产生误差 [z_2]_反=1.111\ 1010(00);产生误差 [z2]反=1.111 1010(00);产生误差
[ z 3 ] 反 = 1.110 0110 ( 01 ) ; 产生误差 [z_3]_反=1.110\ 0110(01);产生误差 [z3]反=1.110 0110(01);产生误差
18.试比较逻辑移位和算术移位。
答:
逻辑移位和算术移位的区别:
逻辑移位是对逻辑数或无符号数进行的移位,其特点是不论左移还是右移,空出位均补0,移位时不考虑符号位。
算术移位是对带符号数进行的移位操作,其关键规则是移位时符号位保持不变,空出位的补入值与数的正负、移位方向、采用的码制等有关。补码或反码右移时具有符号延伸特性。左移时可能产生溢出错误,右移时可能丢失精度。
19.设机器数字长为8位(含1位符号位),用补码运算规则计算下列各题。
(1)A=9/64,B=-13/32,求A+B;
(2)A=19/32,B=-17/128,求A-B;
(3)A=-3/16,B=9/32, 求A+B;
(4)A=-87, B=53, 求A-B;
(5)A=115,B=-24, 求A+B。
答:
( 1 ) A = 9 / 64 = ( 0.001 0010 ) 2 B = − 13 / 32 = ( − 0.011 0100 ) 2 (1)A=9/64=(0.001\ 0010)_2\\ B=-13/32=(-0.011\ 0100)_2 (1)A=9/64=(0.001 0010)2B=−13/32=(−0.011 0100)2
[ A ] 补 = 0.001 0010 [A]_补=0.001\ 0010 [A]补=0.001 0010
[ B ] 补 = 1.100 1100 [B]_补=1.100\ 1100 [B]补=1.100 1100
[ A + B ] 补 = [A+B]_补= [A+B]补=
0.001 0010 + 1.100 1100 1.101 1110 ——无溢出 \begin{array}{c} &0.001\ 0010 \\ +&1.100\ 1100\\ \hline &1.101\ 1110&——无溢出 \\ \end{array} +0.001 00101.100 11001.101 1110——无溢出
A + B = ( − 0.010 0010 ) 2 = − 17 / 64 A+B=(-0.010\ 0010)_2= -17/64 A+B=(−0.010 0010)2=−17/64
( 2 ) A = 19 / 32 = ( 0.100 1100 ) 2 B = − 17 / 128 = ( − 0.001 0001 ) 2 (2)A=19/32=(0.100\ 1100)_2\\ B=-17/128=(-0.001\ 0001)_2 (2)A=19/32=(0.100 1100)2B=−17/128=(−0.001 0001)2
[ A ] 补 = 0.100 1100 [A]_补=0.100\ 1100 [A]补=0.100 1100
[ B ] 补 = 1.110 1111 [B]_补=1.110\ 1111 [B]补=1.110 1111
[ − B ] 补 = 0.001 0001 [-B]_补=0.001\ 0001 [−B]补=0.001 0001
[ A − B ] 补 = [A-B]_补= [A−B]补=
0.100 1100 + 0.001 0001 0.101 1101 ——无溢出 \begin{array}{c} &0.100\ 1100\\ +&0.001\ 0001\\ \hline &0.101\ 1101&——无溢出 \\ \end{array} +0.100 11000.001 00010.101 1101——无溢出
A − B = ( 0.101 1101 ) 2 = 93 / 128 A-B= (0.101\ 1101)_2= 93/128 A−B=(0.101 1101)2=93/128
( 3 ) A = − 3 / 16 = ( − 0.001 1000 ) 2 B = 9 / 32 = ( 0.010 0100 ) 2 (3)A=-3/16=(-0.001\ 1000)_2\\ B=9/32=(0.010\ 0100)_2 (3)A=−3/16=(−0.001 1000)2B=9/32=(0.010 0100)2
[ A ] 补 = 1.110 1000 [A]_补=1.110\ 1000 [A]补=1.110 1000
[ B ] 补 = 0.010 0100 [B]_补=0.010\ 0100 [B]补=0.010 0100
[ A + B ] 补 = [A+B]_补= [A+B]补=
1.110 1000 + 0.010 0100 0.000 1100 ——无溢出 \begin{array}{c} &1.110\ 1000\\ +&0.010\ 0100\\ \hline &0.000\ 1100&——无溢出 \\ \end{array} +1.110 10000.010 01000.000 1100——无溢出
A + B = ( 0.000 1100 ) 2 = 3 / 32 A+B= (0.000\ 1100)_2= 3/32 A+B=(0.000 1100)2=3/32
( 4 ) A = − 87 = ( − 101 0111 ) 2 B = 53 = ( 110 101 ) 2 (4)A=-87=(-101\ 0111)_2\\ B=53=(110\ 101)_2 (4)A=−87=(−101 0111)2B=53=(110 101)2
[ A ] 补 = 1 , 010 1001 [A]_补=1,010\ 1001 [A]补=1,010 1001
[ B ] 补 = 0 , 011 0101 [B]_补=0,011\ 0101 [B]补=0,011 0101
[ − B ] 补 = 1 , 100 1011 [-B]_补=1,100\ 1011 [−B]补=1,100 1011
[ A − B ] 补 = [A-B]_补= [A−B]补=
1 , 010 1001 + 1 , 100 1011 0 , 111 0100 ——溢出 \begin{array}{c} &1,010\ 1001\\ +&1,100\ 1011\\ \hline &0,111\ 0100&——溢出 \\ \end{array} +1,010 10011,100 10110,111 0100——溢出
A − B = ( − 1 , 000 1100 ) 2 = − 140 A-B=(-1,000\ 1100)_2= -140 A−B=(−1,000 1100)2=−140
( 5 ) A = 115 = ( 111 0011 ) 2 B = − 24 = ( − 11 000 ) 2 (5)A=115=(111\ 0011)_2\\ B=-24=(-11\ 000)_2 (5)A=115=(111 0011)2B=−24=(−11 000)2
[ A ] 补 = 0 , 111 0011 [A]_补=0,111\ 0011 [A]补=0,111 0011
[ B ] 补 = 1 , 110 1000 [B]_补=1,110\ 1000 [B]补=1,110 1000
[ A + B ] 补 = [A+B]_补= [A+B]补=
0 , 111 0011 + 1 , 110 1000 0 , 101 1011 ——无溢出 \begin{array}{c} &0,111\ 0011\\ +&1,110\ 1000\\ \hline &0,101\ 1011&——无溢出 \\ \end{array} +0,111 00111,110 10000,101 1011——无溢出
A + B = ( 101 1011 ) 2 = 91 A+B= (101\ 1011)_2= 91 A+B=(101 1011)2=91
注意:
1、单符号位运算要用单符号位的判断方法判溢出;
2、结果的真值形式上要和原始数据一致
20.用原码一位乘、两位乘和补码一位乘(Booth算法)、两位乘计算x·y。
(1)x=0.110 111,y=-0.101 110;
(2)x=-0.010 111,y=-0.010 101:
(3)x=19, y= 35;
(4)x= 0.110 11, y= -0.111 01。
答:
先将数据转换成所需的机器数,然后计算,最后结果转换成真值。 ( 1 ) [ x ] 原 = x = 0.110111 , [ y ] 原 = 1.101110 x ∗ = 0.110111 , y ∗ = 0.101110 x 0 = 0 , y 0 = 1 , z 0 = x 0 ⊕ y 0 = 0 ⊕ 1 = 1 x ∗ × y ∗ = 0.100 111 100 010 先将数据转换成所需的机器数,然后计算,最后结果转换成真值。\\ (1)[x]_原=x=0.110111,[y]_原=1.101110\\ x^*=0.110111,y^*=0.101110 \\ x_0=0,y_0=1,z_0=x_0\oplus y_0=0\oplus 1=1 \\ x^*\times y^*=0.100\ 111\ 100\ 010 先将数据转换成所需的机器数,然后计算,最后结果转换成真值。(1)[x]原=x=0.110111,[y]原=1.101110x∗=0.110111,y∗=0.101110x0=0,y0=1,z0=x0⊕y0=0⊕1=1x∗×y∗=0.100 111 100 010
[ x × y ] 原 = 1.100 111 100 010 x ⋅ y = − 0.100 111 100 010 [x\times y]_原=1.100\ 111\ 100\ 010\\ x·y=-0.100\ 111\ 100\ 010 [x×y]原=1.100 111 100 010x⋅y=−0.100 111 100 010
原码一位乘:
( → 1 表示右移一位 ) (\to 1表示右移一位) (→1表示右移一位)

2 x ∗ = 01.101110 , [ − x ∗ ] 补 = [ − x ] 补 = 1.001001 2x^*=01.101110,[-x^*]_补=[-x]_补=1.001001 2x∗=01.101110,[−x∗]补=[−x]补=1.001001
原码两位乘:

结果同一位乘, x ⋅ y = − 0.100 111 100 010 结果同一位乘,x·y=-0.100\ 111\ 100\ 010 结果同一位乘,x⋅y=−0.100 111 100 010
[ x ] 补 = x = 0.110 111 [x]_补=x=0.110\ 111 [x]补=x=0.110 111
[ y ] 补 = 1.010 010 [y]_补=1.010\ 010 [y]补=1.010 010
[ − x ] 补 = 1.001 001 [-x]_补=1.001\ 001 [−x]补=1.001 001
[ 2 x ] 补 = 01.101 110 [2x]_补=01.101\ 110 [2x]补=01.101 110
[ − 2 x ] 补 = 10.010 010 [-2x]_补=10.010\ 010 [−2x]补=10.010 010
[ x × y ] 补 = 1.011 000 011 110 0 [x\times y]_补=1.011\ 000\ 011\ 110\ 0 [x×y]补=1.011 000 011 110 0
x ⋅ y = − 0.100 111 100 010 0 x·y=-0.100\ 111\ 100\ 010\ 0 x⋅y=−0.100 111 100 010 0
补码一位乘、两位乘运算过程如下 : 补码一位乘、两位乘运算过程如下: 补码一位乘、两位乘运算过程如下:
补码一位乘:

补码两位乘:
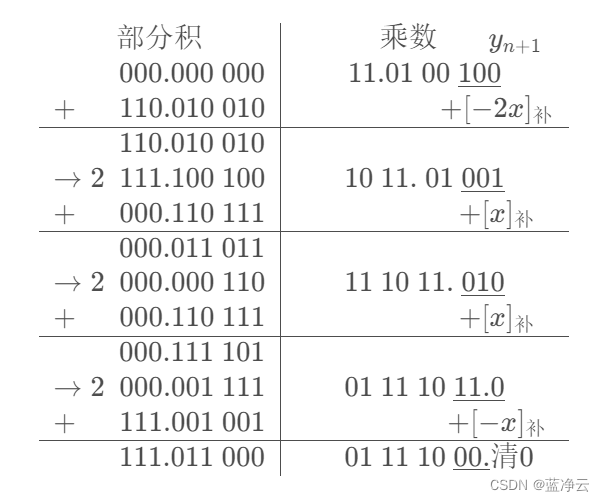
结果同补码一位乘, x ⋅ y = − 0.100 111 100 010 00 结果同补码一位乘,x·y=-0.100\ 111\ 100\ 010\ 00 结果同补码一位乘,x⋅y=−0.100 111 100 010 00
( 2 ) x = − 0.010111 , y = − 0.010101 (2)x=-0.010111, y=-0.010101 (2)x=−0.010111,y=−0.010101
[ x ] 原 = 1.010111 , [ y ] 原 = 1.010101 [x]_原=1.010111, [y]_原=1.010101 [x]原=1.010111,[y]原=1.010101
x ∗ = 0.010111 , y ∗ = 0.010101 x^*=0.010111, y^*=0.010101 x∗=0.010111,y∗=0.010101
[ − x ∗ ] 补 = 1.101001 , 2 x ∗ = 0.101110 [-x^*]_补=1.101001,2x^*=0.101110 [−x∗]补=1.101001,2x∗=0.101110
[ − 2 x ∗ ] 补 = 1.010010 [-2x^*]_补=1.010010 [−2x∗]补=1.010010
x 0 = 1 , y 0 = 1 , z 0 = x 0 ⊕ y 0 = 1 ⊕ 1 = 0 x_0=1,y_0=1,z_0=x_0\oplus y_0=1\oplus 1=0 x0=1,y0=1,z0=x0⊕y0=1⊕1=0
[ x ] 补 = 1.101001 , [ y ] 补 = 1.101011 [x]_补=1.101001,[y]_补=1.101011 [x]补=1.101001,[y]补=1.101011
[ − x ] 补 = 0.010111 , [ 2 x ] 补 = 1.010010 [-x]_补=0.010111,[2x]_补=1.010010 [−x]补=0.010111,[2x]补=1.010010
[ − 2 x ] 补 = 0.101110 [-2x]_补=0.101110 [−2x]补=0.101110
x ∗ × y ∗ = 0.000 111 100 011 x^*\times y^*=0.000\ 111\ 100\ 011 x∗×y∗=0.000 111 100 011
[ x × y ] 原 = 0.000 111 100 011 [x\times y]_原=0.000\ 111\ 100\ 011 [x×y]原=0.000 111 100 011
[ x × y ] 补 = 0.000 111 100 011 0 [x\times y]_补=0.000\ 111\ 100\ 011\ 0 [x×y]补=0.000 111 100 011 0
x ⋅ y = 0.000 111 100 011 x·y= 0.000\ 111\ 100\ 011 x⋅y=0.000 111 100 011
运算过程如下 : 运算过程如下: 运算过程如下:
原码一位乘:
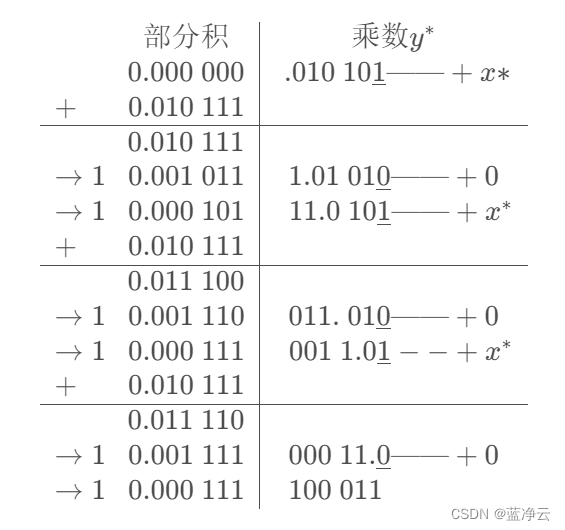
原码两位乘:
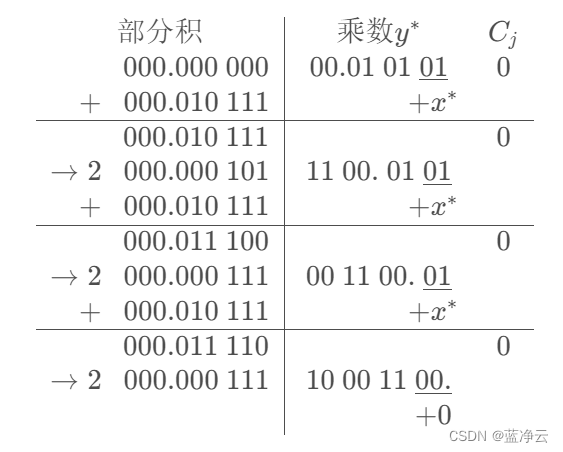
结果同一位乘, x ⋅ y = 0.000 111 100 011 结果同一位乘,x·y= 0.000\ 111\ 100\ 011 结果同一位乘,x⋅y=0.000 111 100 011
补码一位乘:

补码两位乘:
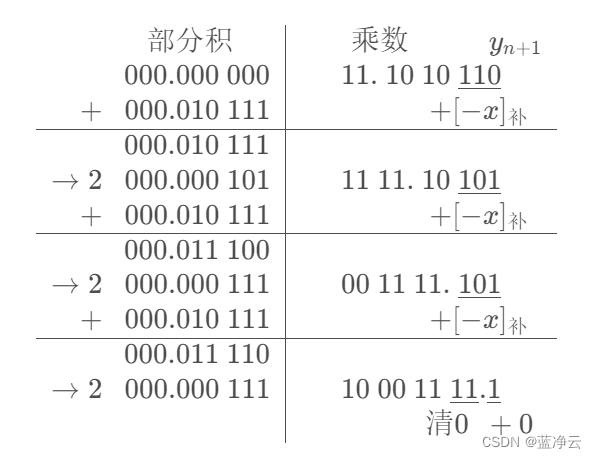
结果同补码一位乘, x ⋅ y = 0.000 111 100 011 00 结果同补码一位乘,x·y= 0.000\ 111\ 100\ 011\ 00 结果同补码一位乘,x⋅y=0.000 111 100 011 00
( 3 ) x = 19 , y = 35 x = ( 10011 ) 2 , y = ( 100 011 ) 2 x ∗ = [ x ] 原 = [ x ] 补 = 0 , 010 011 y ∗ = [ y ] 原 = [ y ] 补 = 0 , 100 011 (3)x=19, y= 35 \\ x=(10 011)_2,y=(100\ 011)_2 \\ x^*=[x]_原=[x]_补=0,010\ 011 \\ y*=[y]_原=[y]_补=0,100\ 011 (3)x=19,y=35x=(10011)2,y=(100 011)2x∗=[x]原=[x]补=0,010 011y∗=[y]原=[y]补=0,100 011
[ − x ∗ ] 补 = [ − x ] 补 = 1 , 101 101 x ∗ = [ 2 x ] 补 = 0 , 100 110 [-x^*]_补=[-x]_补=1,101\ 101\\ x^*= [2x]_补=0,100\ 110 [−x∗]补=[−x]补=1,101 101x∗=[2x]补=0,100 110
[ − 2 x ∗ ] 补 = [ − 2 x ] 补 = 1 , 011 010 x 0 = 0 , y 0 = 0 , z 0 = x 0 ⊕ y 0 = 0 ⊕ 0 = 0 x ⋅ y = x ∗ × y ∗ = [ x × y ] 原 = [ x × y ] 补 = 0 , 001 010 011 001 = ( 665 ) 10 运算过程如下 : [-2x^*]_补=[-2x]_补=1,011\ 010\\ x_0=0,y_0=0,z_0=x_0\oplus y_0=0\oplus0=0 \\ x·y= x^*\times y*= [x\times y]_原= [x\times y]_补=0,001\ 010\ 011\ 001=(665)_{10}\\ 运算过程如下: [−2x∗]补=[−2x]补=1,011 010x0=0,y0=0,z0=x0⊕y0=0⊕0=0x⋅y=x∗×y∗=[x×y]原=[x×y]补=0,001 010 011 001=(665)10运算过程如下:
原码一位乘:
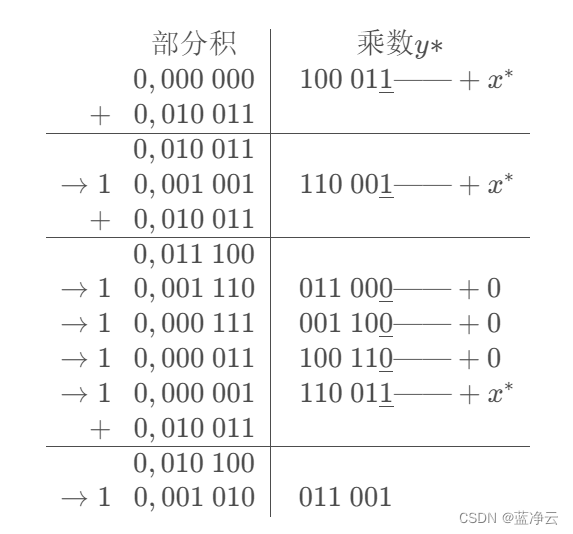
原码两位乘:

结果同一位乘, x ⋅ y = 0 , 001 010 011 001 结果同一位乘,x·y=0,001\ 010\ 011\ 001 结果同一位乘,x⋅y=0,001 010 011 001
补码一位乘:

补码两位乘:

结果同补码一位乘, x ⋅ y = 0 , 001 010 011 001 结果同补码一位乘,x·y= 0,001\ 010\ 011\ 001 结果同补码一位乘,x⋅y=0,001 010 011 001
( 4 ) x = 0.110 11 , y = − 0.111 01 (4)x=0.110\ 11,y=-0.111\ 01 (4)x=0.110 11,y=−0.111 01
x ∗ = [ x ] 原 = [ x ] 补 = 0.110 11 x^*= [x]原= [x]补=0.110\ 11 x∗=[x]原=[x]补=0.110 11
[ y ] 原 = 1.111 01 , y ∗ = 0.111 01 [y]原=1.111\ 01,y^*=0.111\ 01 [y]原=1.111 01,y∗=0.111 01
[ y ] 补 = 1.000 11 [y]补=1.000\ 11 [y]补=1.000 11
[ − x ∗ ] 补 = [ − x ] 补 = 1.001 01 [-x^*]_补=[-x]_补=1.001\ 01 [−x∗]补=[−x]补=1.001 01
2 x ∗ = [ 2 x ] 补 = 01.101 10 2x^*=[2x]_补=01.101\ 10 2x∗=[2x]补=01.101 10
[ − 2 x ∗ ] 补 = [ − 2 x ] 补 = 10.010 10 [-2x^*]_补=[-2x]_补=10.010\ 10 [−2x∗]补=[−2x]补=10.010 10
x 0 = 0 , y 0 = 1 , z 0 = x 0 ⊕ y 0 = 0 ⊕ 1 = 1 x_0=0,y_0=1,z_0=x_0\oplus y_0=0\oplus 1=1 x0=0,y0=1,z0=x0⊕y0=0⊕1=1
x ∗ × y ∗ = 0.110 000 111 1 x^*\times y^*=0.110\ 000\ 111\ 1 x∗×y∗=0.110 000 111 1
[ x × y ] 原 = 1.110 000 111 1 [x\times y]_原=1.110\ 000\ 111\ 1 [x×y]原=1.110 000 111 1
[ x × y ] 补 = 1.001 111 000 10 [x\times y]_补=1.001\ 111\ 000\ 10 [x×y]补=1.001 111 000 10
x ⋅ y = − 0.110 000 111 1 x·y= -0.110\ 000\ 111\ 1 x⋅y=−0.110 000 111 1
运算过程如下 : 运算过程如下: 运算过程如下:
原码一位乘:

原码两位乘:
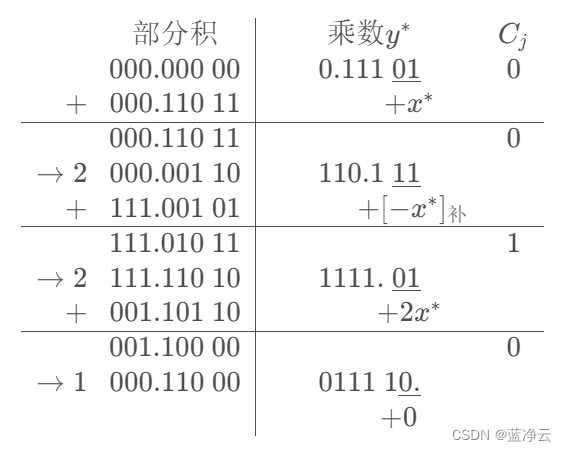
结果同一位乘, x ⋅ y = − 0.110 000 111 1 结果同一位乘,x·y=-0.110\ 000\ 111\ 1 结果同一位乘,x⋅y=−0.110 000 111 1
补码一位乘:
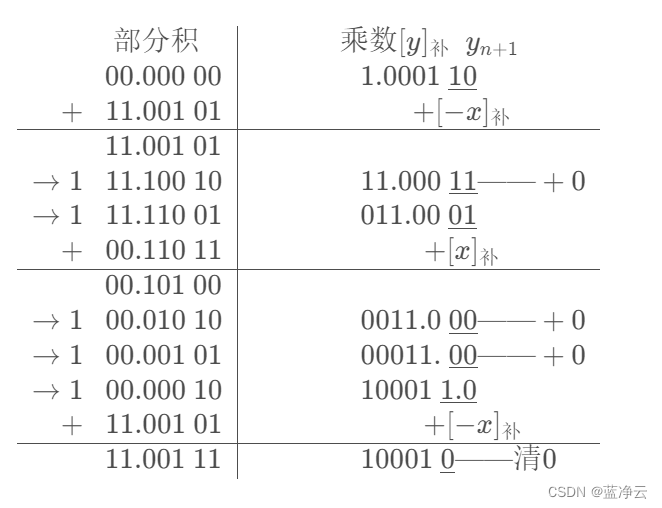
补码两位乘:

结果同补码一位乘, x ⋅ y = − 0.110 000 111 10 结果同补码一位乘,x·y=-0.110\ 000\ 111\ 10 结果同补码一位乘,x⋅y=−0.110 000 111 10
21.用原码加减交替法和补码加减交替法计算 x ÷ y x\div y x÷y。
(1)x=0.100111,y=0.101011;
(2)x=-0.10101,y=0.11011;
(3)x=0.10100, y=-0.10001;
(4)x=13/32, y=-27/32。
答:
( 1 ) x ∗ = [ x ] 原 = [ x ] 补 = x = 0.100 111 y ∗ = [ y ] 原 = [ y ] 补 = y = 0.101 011 (1)x^*=[x]_原=[x]_补=x=0.100\ 111\\ y^*=[y]_原=[y]_补=y=0.101\ 011 (1)x∗=[x]原=[x]补=x=0.100 111y∗=[y]原=[y]补=y=0.101 011
[ − y ∗ ] 补 = [ − y ] 补 = 1.010 101 [-y^*]_补=[-y]_补=1.010\ 101 [−y∗]补=[−y]补=1.010 101
q 0 = x 0 ⊕ y 0 = 0 ⊕ 0 = 0 x ÷ y = x ∗ ÷ y ∗ = [ x ÷ y ] 原 = 0.111 010 r ∗ = 0.000 010 × 2 − 6 = 0.000 000 000 010 计算过程如下 : q_0=x_0\oplus y_0=0 \oplus 0=0\\ x\div y=x^*\div y^*=[x\div y]_原=0.111\ 010\\ r^*=0.000\ 010\times2^{-6}=0.000\ 000\ 000\ 010\\ 计算过程如下: q0=x0⊕y0=0⊕0=0x÷y=x∗÷y∗=[x÷y]原=0.111 010r∗=0.000 010×2−6=0.000 000 000 010计算过程如下:
原码加减交替除法:

补码加减交替除法:

注 : 恒置 1 引入误差。 x ÷ y = [ x ÷ y ] 补 = 0.111 011 注:恒置1引入误差。\\ x\div y=[x\div y]_补= 0.111\ 011 注:恒置1引入误差。x÷y=[x÷y]补=0.111 011
[ r ] 补 = 0.000 010 , r = r ∗ = 0.000 000 000 010 [r]_补=0.000\ 010,r=r^*=0.000\ 000\ 000\ 010 [r]补=0.000 010,r=r∗=0.000 000 000 010
( 2 ) x = − 0.101 01 , y = 0.110 11 (2)x=-0.101 \ 01,y=0.110\ 11 (2)x=−0.101 01,y=0.110 11
[ x ] 原 = 1.101 01 x ∗ = 0.101 01 y ∗ = [ y ] 原 = [ y ] 补 = y = 0.110 11 [x]_原=1.101\ 01 \\ x^*=0.101\ 01\\ y^*=[y]_原=[y]_补=y=0.110\ 11 [x]原=1.101 01x∗=0.101 01y∗=[y]原=[y]补=y=0.110 11
[ − y ∗ ] 补 = [ − y ] 补 = 1.001 01 [-y^*]_补=[-y]_补=1.001\ 01 [−y∗]补=[−y]补=1.001 01
[ x ] 补 = 1.010 11 q 0 = x 0 ⊕ y 0 = 1 ⊕ 0 = 1 x ∗ ÷ y ∗ = 0.110 00 [x]_补=1.010\ 11\\ q_0=x_0\oplus y_0=1\oplus 0=1 \\ x^*\div y^*= 0.110\ 00 [x]补=1.010 11q0=x0⊕y0=1⊕0=1x∗÷y∗=0.110 00
[ x ÷ y ] 原 = 1.110 00 x ÷ y = − 0.110 00 r ∗ = 0.110 00 × 2 − 5 = 0.000 001 100 0 计算过程如下 : [x\div y]_原=1.110\ 00 \\ x\div y=-0.110\ 00 \\ r^*=0.110\ 00\times 2^{-5}=0.000\ 001\ 100\ 0\\ 计算过程如下: [x÷y]原=1.110 00x÷y=−0.110 00r∗=0.110 00×2−5=0.000 001 100 0计算过程如下:
原码加减交替除法:


注 : 恒置 1 引入误差。 注:恒置1引入误差。 注:恒置1引入误差。
[ r ] 补 = 1.010 00 , r = − 0.000 001 100 0 [r]_补=1.010\ 00, r=-0.000\ 001\ 100\ 0 [r]补=1.010 00,r=−0.000 001 100 0
[ x ÷ y ] 补 = 1.001 11 , x ÷ y = − 0.110 01 [x\div y]_补=1.001\ 11,x\div y= -0.110\ 01 [x÷y]补=1.001 11,x÷y=−0.110 01
( 3 ) x = 0.101 00 , y = − 0.100 01 x ∗ = [ x ] 原 = [ x ] 补 = x = 0.101 00 (3)x=0.101\ 00,y=-0.100\ 01\\ x^*=[x]_原=[x]_补=x=0.101\ 00 (3)x=0.101 00,y=−0.100 01x∗=[x]原=[x]补=x=0.101 00
[ y ] 原 = 1.100 01 y ∗ = 0.100 01 [y]_原=1.100\ 01 \\ y^*=0.100\ 01 [y]原=1.100 01y∗=0.100 01
[ − y ∗ ] 补 = 1.011 11 [-y^*]_补=1.011\ 11 [−y∗]补=1.011 11
[ y ] 补 = 1.011 11 [y]_补=1.011\ 11 [y]补=1.011 11
[ − y ] 补 = 0.100 01 q 0 = x 0 ⊕ y 0 = 0 ⊕ 1 = 1 x ∗ ÷ y ∗ = 1.001 01 ——溢出 [-y]_补=0.100\ 01\\ q_0=x_0\oplus y_0=0\oplus 1=1 \\ x^*\div y^*= 1.001\ 01 —— 溢出 [−y]补=0.100 01q0=x0⊕y0=0⊕1=1x∗÷y∗=1.001 01——溢出
[ x ÷ y ] 原 : 无定义 x ÷ y = − 1.001 01 r ∗ = 0.010 11 × 2 − 5 = 0.000 000 101 1 计算过程如下 : [x\div y]_原:无定义 \\ x\div y=-1.001\ 01 \\ r^*=0.010\ 11\times 2^{-5}=0.000\ 000\ 101\ 1\\ 计算过程如下: [x÷y]原:无定义x÷y=−1.001 01r∗=0.010 11×2−5=0.000 000 101 1计算过程如下:
原码加减交替除法:

注:溢出,可停止运算,转溢出处理。
注:当 x ∗ > y ∗ x^*>y^* x∗>y∗时产生溢出,这种情况在第一步运算后判断r的正负时就可发现。此时数值位占领小数点左边的1位,原码无定义,但算法本身仍可正常运行。
补码加减交替除法:

注:由于本题中 x ∗ > y ∗ x^*>y^* x∗>y∗,有溢出。除法运算时一般在运算前判断是否 x ∗ > y ∗ x^*>y^* x∗>y∗,如果该条件成立则停止运算,转溢出处理。但此算法本身在溢出情况下仍可正常运行,此时数值位占领小数点左边的1位,商需设双符号位(变形补码),以判溢出。采用这种方法时运算前可不判溢出,直接进行运算,运算完后再判溢出。
( 4 ) x = 13 / 32 = ( 0.011 01 ) 2 y = − 27 / 32 = ( − 0.110 11 ) 2 x ∗ = [ x ] 原 = [ x ] 补 = x = 0.011 01 (4)x=13/32=(0.011\ 01)_2\\ y=-27/32=(-0.110\ 11)_2 \\ x^*= [x]_原= [x]_补=x=0.011\ 01 (4)x=13/32=(0.011 01)2y=−27/32=(−0.110 11)2x∗=[x]原=[x]补=x=0.011 01
[ y ] 原 = 1.110 11 y ∗ = 0.110 11 [y]_原=1.110\ 11 \\ y^* =0.110\ 11 [y]原=1.110 11y∗=0.110 11
[ − y ∗ ] 补 = 1.001 01 [-y^*]_补=1.001\ 01 [−y∗]补=1.001 01
[ y ] 补 = 1.001 01 [y]_补=1.001\ 01 [y]补=1.001 01
[ − y ] 补 = 0.110 11 q 0 = x 0 ⊕ y 0 = 0 ⊕ 1 = 1 x ∗ ÷ y ∗ = 0.011 11 [-y]_补=0.110\ 11\\ q_0=x_0\oplus y_0=0\oplus1=1 \\ x^*\div y^*= 0.011\ 11 [−y]补=0.110 11q0=x0⊕y0=0⊕1=1x∗÷y∗=0.011 11
[ x ÷ y ] 原 = 1.011 11 x ÷ y = ( − 0.011 11 ) 2 = − 15 / 32 r ∗ = 0.010 11 × 2 − 5 = 0.000 000 101 1 [x\div y]_原=1.011\ 11\\ x\div y=(-0.011\ 11)_2= -15/32 \\ r^*=0.010\ 11\times2^{-5}=0.000\ 000\ 101\ 1 [x÷y]原=1.011 11x÷y=(−0.011 11)2=−15/32r∗=0.010 11×2−5=0.000 000 101 1
原码加减交替除法:

补码加减交替除法:

[ r ] 补 = 0.010 11 , r = r ∗ = 0.000 000 101 1 [r]_补=0.010\ 11,r=r^*=0.000\ 000\ 101\ 1 [r]补=0.010 11,r=r∗=0.000 000 101 1
[ x ÷ y ] 补 = 1.100 01 , x ÷ y = ( − 0.011 11 ) 2 = − 15 / 32 [x\div y]_补=1.100\ 01,x\div y=(-0.011\ 11)_2=-15/32 [x÷y]补=1.100 01,x÷y=(−0.011 11)2=−15/32
22.设机器字长为16位(含1位符号位),若一次移位需 1 μ s 1\mu s 1μs,一次加法需 1 μ s 1\mu s 1μs,试问原码一位乘、补码一位乘、原码加减交替除和补码加减交替除法最多各需多少时间?
答:
原码一位乘最多需时 = 1 μ s × 15 ( 加 ) + 1 μ s × 15 ( 移位 ) = 30 μ s 补码一位乘最多需时 = 1 μ s × 16 + 1 μ s × 15 = 31 μ s 原码加减交替除最多需时 = 1 μ s × ( 16 + 1 ) + 1 μ s × 15 = 32 μ s 补码加减交替除最多需时 = 1 μ s × ( 16 + 1 ) + 1 μ s × 15 = 32 μ s 原码一位乘最多需时=1\mu s\times 15(加)+1\mu s\times 15(移位)=30\mu s\\ 补码一位乘最多需时=1\mu s\times 16+1\mu s\times 15=31\mu s\\ 原码加减交替除最多需时=1\mu s\times (16+1)+1\mu s\times 15=32\mu s\\ 补码加减交替除最多需时=1\mu s\times (16+1)+1\mu s\times 15=32\mu s 原码一位乘最多需时=1μs×15(加)+1μs×15(移位)=30μs补码一位乘最多需时=1μs×16+1μs×15=31μs原码加减交替除最多需时=1μs×(16+1)+1μs×15=32μs补码加减交替除最多需时=1μs×(16+1)+1μs×15=32μs
23.画出实现 Booth算法的运算器框图。
要求如下:
(1) 寄存器和全加器均用方框表示,指出寄存器和全加器的位数.
(2)说明加和移位的次数。
(3)详细画出最低位全加器的输入电路.
(4)描述 Booth算法重复加和移位的过程。
答:
(1)实现补码Booth算法的运算器框图如下图所示。图中全加器和寄存器均为n+2位,其中A寄存器存放部分积,含两位符号位,初态为“0”;X寄存器存放被乘数的补码,含两位符号位;Q寄存器存放乘数的补码,含1位符号位,最末位为附加位,初态为“0”。最终乘积的高位在寄存器A中,乘积的低位在Q寄存器中。计数器C用来控制移位次数,判断乘法是否结束。 G M G_M GM为乘法标记。
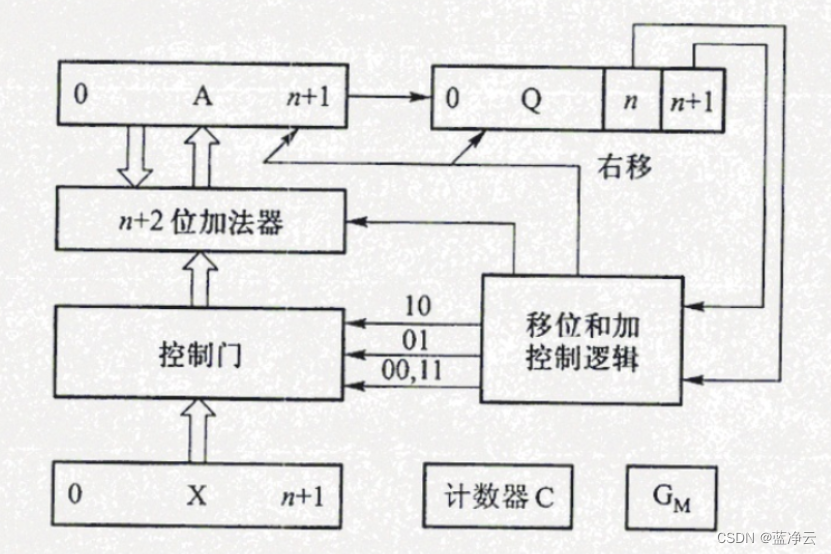
(2)Booth算法共做n次移位,最多做n+1次加法。
(3)最低位全加器的输入电路如下图所示。
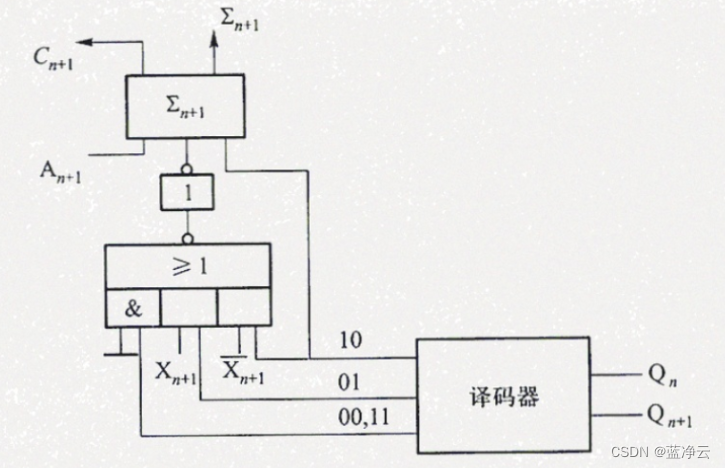
(4)加的过程受Q寄存器末两位控制,当它们同时为0(记做 Q n ‾ Q n + 1 ‾ \overline {Q_n} \ \overline{Q_{n+1}} Qn Qn+1)或同时为1(记做 Q n Q n + 1 Q_n Q_{n+1} QnQn+1)时,部分积(在A中)不变;当末两位为01(记做 Q n ‾ Q n + 1 \overline {Q_n} Q_{n+1} QnQn+1)时,部分积加上被乘数(记做A+X);
当末两位为10(记做 Q n Q n + 1 ‾ Q_n \overline {Q_{n+1}} QnQn+1)时,部分积减去被乘数,即与求补后的被乘数相加(记做 A + X ‾ + 1 A+\overline X+1 A+X+1)。
则Booth 算法的重复加过程可描述为:
( Q n ‾ Q n + 1 ‾ + Q n Q n + 1 ) A + Q n ‾ Q n + 1 ( A + X ) + Q n Q n + 1 ‾ ( A + X ‾ + 1 ) → A (\overline {Q_n} \ \overline{Q_{n+1}}+Q_n Q_{n+1})A+\overline {Q_n} Q_{n+1}(A+X)+Q_n \overline {Q_{n+1}}(A+\overline X+1)→A (Qn Qn+1+QnQn+1)A+QnQn+1(A+X)+QnQn+1(A+X+1)→A
移位时A、Q两个寄存器串接(A//Q),一起右移一位(算术移位),记L(A//Q)→R(A//Q)。
24.画出实现补码加减交替法的运算器框图。
要求如下:
(1)寄存器和全加器均用方框表示,指出寄存器和全加器的位数。
(2)说明加和移位的次数。
(3)详细画出第5位(设n为最低位)全加器的输入电路。
(4)画出上商的输入电路。
(5)描述商符的形成过程。
答:
(1)补码加减交替法的运算框图:图中全加器n+1位,寄存器A存放被除数,n+1位(含一位符号位);寄存器X存放除数,n+1位(含一位符号位);寄存器Q存放商,n+1位(含一位符号位),初态为0.
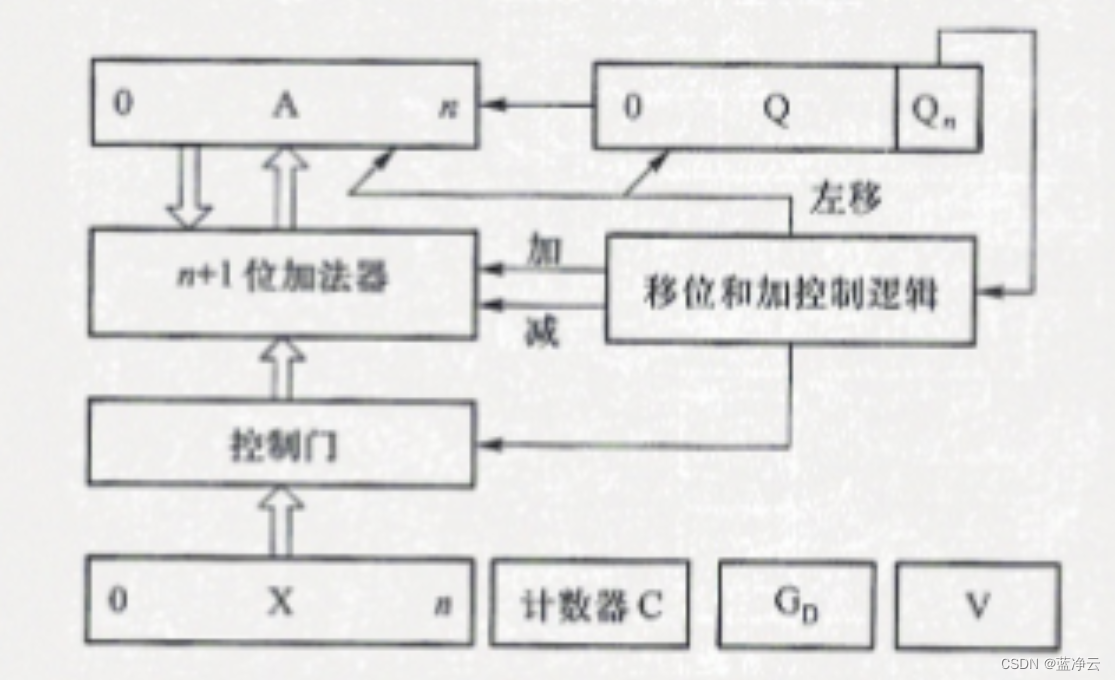
(2)加操作: Q n ( A + X ‾ + 1 ) + Q n ‾ ( A + X ) → A Q_n(A+\overline X+1)+\overline{Q_n}(A+X)→A Qn(A+X+1)+Qn(A+X)→A
(3)第5位全加器的输入电路:
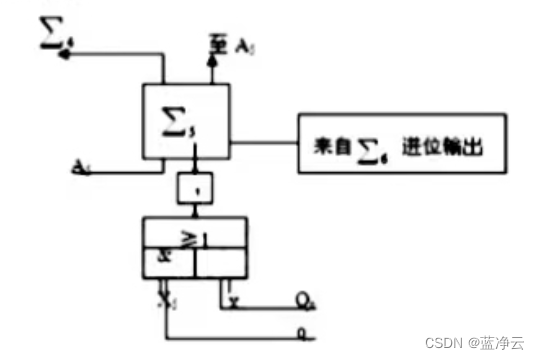
(4)上商的输入电路:

(5)商符的形成: A 0 ⊕ X 0 ‾ → Q n \overline{A_0\oplus X_0}→Q_n A0⊕X0→Qn
25.对于尾数为40位的浮点数(不包括符号位在内),若采用不同的机器数表示,试问当尾数左规或右规时,最多移位次数各为多少?
答:
对于尾数为40位的浮点数,若采用原码表示,当尾数左规时,最多移位39次;反码表示时情况同原码;若采用补码表示,当尾数左规时,正数最多移位39次,同原码;负数最多移位40次。当尾数右规时,不论采用何种码制,均只需右移1次。
26.按机器补码浮点运算步骤计算 [ x ± y ] 补 [x\pm y]_补 [x±y]补
( 1 ) x = 2 − 011 × 0.101 100 , y = 2 − 010 × ( − 0.011 100 ) ; ( 2 ) x = 2 − 011 × ( − 0.100 010 ) , y = 2 − 010 × ( − 0.011 111 ) ; ( 3 ) x = 2 101 × ( − 0.100 101 ) , y = 2 100 × ( − 0.001 111 ) 。 (1)x=2^{-011}\times 0.101\ 100, y=2^{-010}\times (-0.011\ 100);\\ (2) x=2^{-011}\times (-0.100\ 010),y=2^{-010}\times (-0.011\ 111);\\ (3)x=2^{101}\times (-0.100\ 101),y=2^{100}\times (-0.001\ 111)。 (1)x=2−011×0.101 100,y=2−010×(−0.011 100);(2)x=2−011×(−0.100 010),y=2−010×(−0.011 111);(3)x=2101×(−0.100 101),y=2100×(−0.001 111)。
答:
先将 x 、 y 转换成机器数形式 : ( 1 ) [ x ] 补 = 1 , 101 ; 0.101 100 先将x、y转换成机器数形式:\\ (1)[x]_补=1,101;0.101\ 100 先将x、y转换成机器数形式:(1)[x]补=1,101;0.101 100
[ y ] 补 = 1 , 110 ; 1.100 100 [y]_补=1,110;1.100\ 100 [y]补=1,110;1.100 100
注:为简单起见,源操作数可直接写成浮点格式,不必规格化。
1 ) 对阶 : 1)对阶: 1)对阶:
[ Δ E ] 补 = [ E x ] 补 + [ − E y ] 补 = 11 , 101 + 00 , 010 = 11 , 111 [\Delta E]_补=[E_x]_补+[-E_y]_补=11,101+00,010=11,111 [ΔE]补=[Ex]补+[−Ey]补=11,101+00,010=11,111
[ Δ E ] 补 < 0 ,应 E x 向 E y 对齐,则 : [\Delta E]_补<0,应E_x向E_y对齐,则: [ΔE]补<0,应Ex向Ey对齐,则:
[ E x ] 补 + 1 = 11 , 101 + 00 , 001 = 11 , 110 [E_x]_补+1=11,101+00,001=11,110 [Ex]补+1=11,101+00,001=11,110
[ Δ E ] 补 + 1 = 11 , 111 + 00 , 001 = 00 , 000 = 0 [\Delta E]_补+1=11,111+00,001=00,000=0 [ΔE]补+1=11,111+00,001=00,000=0
至此, E x = E y ,对毕。 至此, E_x=E_y,对毕。 至此,Ex=Ey,对毕。
[ x ] 补 = 1 , 110 ; 0.010 110 [x]_补=1,110;0.010\ 110 [x]补=1,110;0.010 110
2 ) 尾数运算 : 2)尾数运算: 2)尾数运算:
[ M x ] 补 + [ M y ] 补 = [M_x]_补+[M_y]_补= [Mx]补+[My]补=
00.010 110 + 11.100 100 11.111 010 \begin{array}{c} & 00.010\ 110 \\ + &11.100\ 100\\ \hline & 11.111\ 010 \end{array} +00.010 11011.100 10011.111 010
[ M x ] 补 + [ − M y ] 补 = [M_x]_补+[-M_y]_补= [Mx]补+[−My]补=
00.010 110 + 00.011 100 00.110 010 \begin{array}{c} & 00.010\ 110 \\ + &00.011\ 100\\ \hline & 00.110\ 010 \end{array} +00.010 11000.011 10000.110 010
3 ) 结果规格化 : 3)结果规格化: 3)结果规格化:
[ x + y ] 补 = 11 , 110 ; 11.111 010 = 11 , 011 ; 11.010 000 [x+y]_补=11,110;11.111\ 010 =11,011; 11.010\ 000 [x+y]补=11,110;11.111 010=11,011;11.010 000
( 左规 3 次,阶码减 3 ,尾数左移 3 位 ) (左规3次,阶码减3,尾数左移3位) (左规3次,阶码减3,尾数左移3位)
[ x − y ] 补 = 11 , 110 ; 00.110 010 已是规格化数。 4 ) 舍入 : 无 5 ) 溢出 : 无 则 : x + y = 2 − 101 × ( − 0.110 000 ) x − y = 2 − 010 × 0.110 010 [x-y]_补=11,110;00.110\ 010 已是规格化数。\\ 4)舍入:无\\ 5)溢出:无\\ 则:x+y=2^{-101}\times(-0.110\ 000)\\ x-y =2^{-010}\times 0.110\ 010 [x−y]补=11,110;00.110 010已是规格化数。4)舍入:无5)溢出:无则:x+y=2−101×(−0.110 000)x−y=2−010×0.110 010
( 2 ) x = 2 − 011 × ( − 0.100010 ) y = 2 − 010 × ( − 0.011111 ) (2)x=2^{-011}\times (-0.100010)\\ y=2^{-010}\times (-0.011111) (2)x=2−011×(−0.100010)y=2−010×(−0.011111)
[ x ] 补 = 1 , 101 ; 1.011 110 [x]_补=1,101;1.011\ 110 [x]补=1,101;1.011 110
[ y ] 补 = 1 , 110 ; 1.100 001 [y]_补=1,110;1.100\ 001 [y]补=1,110;1.100 001
1 ) 对阶 : 过程同 1 ) ,则 1)对阶:\\ 过程同1),则 1)对阶:过程同1),则
[ x ] 补 = 1 , 110 ; 1.101 111 2 ) 尾数运算 : [x]_补=1,110;1.101\ 111\\ 2)尾数运算: [x]补=1,110;1.101 1112)尾数运算:
[ M x ] 补 + [ M y ] 补 = [M_x]_补+[M_y]_补= [Mx]补+[My]补=
11.101 111 + 11.100 001 11.010 000 \begin{array}{c} & 11.101\ 111 \\ + &11.100\ 001\\ \hline &11.010\ 000 \end{array} +11.101 11111.100 00111.010 000
[ M x ] 补 + [ − M y ] 补 = [M_x]_补+[-M_y]_补= [Mx]补+[−My]补=
11.101 111 + 00.011 111 00.001 110 \begin{array}{c} &11.101\ 111 \\ + &00.011\ 111\\ \hline & 00.001\ 110 \end{array} +11.101 11100.011 11100.001 110
3 ) 结果规格化 : 3)结果规格化: 3)结果规格化:
[ x + y ] 补 = 11 , 110 ; 11.010 000 已是规格化数。 [x+y]_补=11,110;11.010\ 000已是规格化数。 [x+y]补=11,110;11.010 000已是规格化数。
[ x − y ] 补 = 11 , 110 ; 00.001 110 = 11 , 100 ; 00.111 000 [x-y]_补=11,110;00.001\ 110=11,100; 00.111\ 000 [x−y]补=11,110;00.001 110=11,100;00.111 000
( 左规 2 次,阶码减 2 ,尾数左移 2 位 ) 4 ) 舍入 : 无 5 ) 溢出 : 无 则 : x + y = 2 − 010 × ( − 0.110 000 ) x − y = 2 − 100 × 0.111 000 (左规2次,阶码减2,尾数左移2位)\\ 4)舍入:无\\ 5)溢出:无\\ 则:x+y=2^{-010}\times(-0.110\ 000)\\ x-y =2^{-100}\times 0.111\ 000 (左规2次,阶码减2,尾数左移2位)4)舍入:无5)溢出:无则:x+y=2−010×(−0.110 000)x−y=2−100×0.111 000
( 3 ) x = 2 101 × ( − 0100 101 ) y = 2 100 × ( − 0.001 111 ) (3)x=2^{101}\times (-0100\ 101)\\ y=2^{100}\times (-0.001\ 111) (3)x=2101×(−0100 101)y=2100×(−0.001 111)
[ x ] 补 = 0 , 101 ; 1.011 011 [x]_补=0,101;1.011\ 011 [x]补=0,101;1.011 011
[ y ] 补 = 0 , 100 ; 1.110 001 [y]_补=0,100;1.110\ 001 [y]补=0,100;1.110 001
1 ) 对阶 : 1)对阶: 1)对阶:
[ Δ E ] 补 = [ E x ] 补 + [ − E y ] 补 = 00 , 101 + 11 , 100 = 00 , 001 [\Delta E]_补=[E_x]_补+[-E_y]_补=00,101+11,100=00,001 [ΔE]补=[Ex]补+[−Ey]补=00,101+11,100=00,001
[ Δ E ] 补 > 0 ,应 E y 向 E x 对齐,则 : [\Delta E]_补>0,应E_y向E_x对齐,则: [ΔE]补>0,应Ey向Ex对齐,则:
[ E y ] 补 + 1 = 00 , 100 + 00 , 001 = 00 , 101 [E_y]_补+1=00,100+00,001=00,101 [Ey]补+1=00,100+00,001=00,101
[ E ] 补 + [ − 1 ] 补 = 00 , 001 + 11 , 111 = 00 , 000 = 0 至此, E y = E x ,对毕。 [E]_补+[-1]_补=00,001+11,111=00,000=0\\ 至此, E_y=E_x,对毕。 [E]补+[−1]补=00,001+11,111=00,000=0至此,Ey=Ex,对毕。
[ y ] 补 = 0 , 101 ; 1.111 000 ( 1 ) 2 ) 尾数运算 : [y]补=0,101;1.111\ 000 (1)\\ 2)尾数运算: [y]补=0,101;1.111 000(1)2)尾数运算:
[ M x ] 补 + [ M y ] 补 = [M_x]_补+[M_y]_补= [Mx]补+[My]补=
11.011 011 + 11.111 000 ( 1 ) 11.010 011 ( 1 ) \begin{array}{c} &11.011\ 011 \\ + &11.111\ 000&(1)\\ \hline & 11.010\ 011&(1) \end{array} +11.011 01111.111 00011.010 011(1)(1)
[ M x ] 补 + [ − M y ] 补 = [M_x]_补+[-M_y]_补= [Mx]补+[−My]补=
11.011 011 + 00.000 111 ( 1 ) 11.100 010 ( 1 ) \begin{array}{c} &11.011\ 011 \\ + &00.000\ 111& (1)\\ \hline & 11.100\ 010&(1) \end{array} +11.011 01100.000 11111.100 010(1)(1)
3 ) 结果规格化 : 3)结果规格化: 3)结果规格化:
[ x + y ] 补 = 00 , 101 ; 11.010 011 ( 1 ) 已是规格化数。 [x+y]_补=00,101;11.010\ 011 (1)已是规格化数。 [x+y]补=00,101;11.010 011(1)已是规格化数。
[ x − y ] 补 = 00 , 101 ; 11.100 010 ( 1 ) = 00 , 100 ; 11.000 101 ( 左规 1 次,阶码减 1 ,尾数左移 1 位 ) 4 ) 舍入 : [x-y]_补=00,101;11.100\ 010 (1)=00,100; 11.000\ 101\\ (左规1次,阶码减1,尾数左移1位)\\ 4)舍入: [x−y]补=00,101;11.100 010(1)=00,100;11.000 101(左规1次,阶码减1,尾数左移1位)4)舍入:
[ x + y ] 补 = 00 , 101 ; 11.010 011 ( 舍 ) [x+y]_补=00,101;11.010\ 011(舍) [x+y]补=00,101;11.010 011(舍)
[ x − y ] 补 不变。 [x-y]_补不变。 [x−y]补不变。
[ x − y ] 补 = 00 , 100 ; 11.000 101 [x-y]_补=00,100;11.000\ 101 [x−y]补=00,100;11.000 101
5 ) 溢出 : 无 则 : x + y = 2 101 × ( − 0.101 101 ) x − y = 2 100 × ( − 0.111 011 ) 5)溢出:无\\ 则:x+y=2^{101}\times(-0.101\ 101)\\ x-y =2^{100}\times(-0.111\ 011) 5)溢出:无则:x+y=2101×(−0.101 101)x−y=2100×(−0.111 011)
27.假设阶码取3位,尾数取6位(均不包括符号位),计算下列各题。
( 1 ) [ 2 5 × ( 11 / 16 ) ] + [ 2 4 × ( − 9 / 16 ) ] ( 2 ) [ 2 − 3 × ( 13 / 16 ) ] − [ 2 − 4 × ( − 5 / 8 ) ] ( 3 ) [ 2 3 × ( 13 / 16 ) ] × [ 2 4 × ( − 9 / 16 ) ] ( 4 ) [ 2 6 × ( − 11 / 16 ) ] ÷ [ 2 3 × ( − 15 / 16 ) ] ( 5 ) [ 2 3 × ( − 1 ) ] × [ 2 − 2 × 57 / 64 ] ( 6 ) [ 2 − 6 × ( − 1 ) ] ÷ [ 2 7 × ( − 1 / 2 ) ] ( 7 ) 3.3125 + 6.125 ( 8 ) 1475 − 24375 (1)[2^5\times (11/16)]+[2^4\times (-9/16)]\\ (2)[2^{-3}\times (13/16)]-[2^{-4}\times (-5/8)]\\ (3)[2^3\times (13/16)]\times [2^4\times (-9/16)]\\ (4)[2^6\times (-11/16)]\div[2^3\times (-15/16)]\\ (5)[2^3\times (-1)]\times [2^{-2}\times 57/64]\\ (6)[2^{-6}\times (-1)]\div[2^7\times (-1/2)]\\ (7)3.3125+6.125\\ (8)1475-24375 (1)[25×(11/16)]+[24×(−9/16)](2)[2−3×(13/16)]−[2−4×(−5/8)](3)[23×(13/16)]×[24×(−9/16)](4)[26×(−11/16)]÷[23×(−15/16)](5)[23×(−1)]×[2−2×57/64](6)[2−6×(−1)]÷[27×(−1/2)](7)3.3125+6.125(8)1475−24375
答:
设机器数采用阶补尾补形式 : ( 1 ) x = 2 5 × ( 11 / 16 ) = 2 101 × 0.10 1100 y = 2 4 × ( − 9 / 16 ) = 2 100 × ( − 0.10 0100 ) 则 : [ x ] 阶补尾补 = 00 , 101 ; 00.10 1100 设机器数采用阶补尾补形式:\\ (1)x=2^5\times (11/16)=2^{101}\times 0.10\ 1100\\ y= 2^4\times (-9/16)=2^{100}\times (-0.10\ 0100)\\ 则:[x]_{阶补尾补}=00,101;00.10\ 1100 设机器数采用阶补尾补形式:(1)x=25×(11/16)=2101×0.10 1100y=24×(−9/16)=2100×(−0.10 0100)则:[x]阶补尾补=00,101;00.10 1100
[ y ] 阶补尾补 = 00 , 100 ; 11.01 1100 1 ) 对阶 : [y]_{阶补尾补}=00,100;11.01\ 1100\\ 1)对阶: [y]阶补尾补=00,100;11.01 11001)对阶:
[ Δ E ] 补 = [ E x ] 补 + [ − E y ] 补 = 00 , 101 + 11 , 100 = 00 , 001 [\Delta E]_补=[E_x]_补+[-E_y]_补=00,101+11,100=00,001 [ΔE]补=[Ex]补+[−Ey]补=00,101+11,100=00,001
[ Δ E ] 补 > 0 ,应 E y 向 E x 对齐,则 : [\Delta E]_补>0,应E_y向E_x对齐,则: [ΔE]补>0,应Ey向Ex对齐,则:
[ E y ] 补 + 1 = 00 , 100 + 00 , 001 = 00 , 101 [E_y]_补+1=00,100+00,001=00,101 [Ey]补+1=00,100+00,001=00,101
[ Δ E ] 补 + [ − 1 ] 补 = 00 , 001 + 11 , 111 = 0 [\Delta E]_补+[-1]_补=00,001+11,111=0 [ΔE]补+[−1]补=00,001+11,111=0
至此, E y = E x ,对毕。 至此,E_y=E_x,对毕。 至此,Ey=Ex,对毕。
[ y ] 补 = 00 , 101 ; 11.10 1110 2 ) 尾数运算 : [y]_补=00,101;11.10\ 1110\\ 2)尾数运算: [y]补=00,101;11.10 11102)尾数运算:
[ M x ] 补 + [ M y ] 补 = [M_x]_补+[M_y]_补= [Mx]补+[My]补=
00.10 1100 + 11.10 1110 00.01 1010 \begin{array}{c} &00.10\ 1100 \\ +&11.10\ 1110\\ \hline & 00.01\ 1010 \\ \end{array} +00.10 110011.10 111000.01 1010
3 ) 结果规格化 : 左规 1 位 3)结果规格化:左规1位 3)结果规格化:左规1位
[ x + y ] 补 = 00 , 101 ; 00.011 010 = 00 , 100 ; 00.110 100 [x+y]_补=00,101;00.011\ 010=00,100;00.110\ 100 [x+y]补=00,101;00.011 010=00,100;00.110 100
4 ) 舍入 : 不需舍入。 5 ) 溢出 : 无 则 : x + y = 2 100 × ( 0.110 100 ) = 2 4 × ( 13 / 16 ) 4)舍入:不需舍入。\\ 5)溢出:无\\ 则:x+y=2^{100}\times (0.110\ 100)=2^4\times (13/16) 4)舍入:不需舍入。5)溢出:无则:x+y=2100×(0.110 100)=24×(13/16)
( 2 ) [ 2 − 3 × ( 13 / 16 ) ] − [ 2 − 4 × ( − 5 / 8 ) ] x = 2 − 3 × ( 13 / 16 ) = 2 − 011 × 0.110 100 y = 2 − 4 × ( − 5 / 8 ) = 2 − 100 × ( − 0.101 000 ) (2)[2^{-3}\times (13/16)]-[2^{-4}\times (-5/8)]\\ x=2^{-3}\times (13/16)=2^{-011}\times 0.110\ 100 \\ y= 2^{-4}\times (-5/8)=2^{-100}\times (-0.101\ 000) (2)[2−3×(13/16)]−[2−4×(−5/8)]x=2−3×(13/16)=2−011×0.110 100y=2−4×(−5/8)=2−100×(−0.101 000)
[ x ] 阶补尾补 = 11 , 101 ; 00.110 100 [x]_{阶补尾补}=11,101;00.110\ 100 [x]阶补尾补=11,101;00.110 100
[ y ] 阶补尾补 = 11 , 100 ; 11.011 000 1 ) 对阶 : [y]_{阶补尾补}=11,100;11.011\ 000\\ 1)对阶: [y]阶补尾补=11,100;11.011 0001)对阶:
[ Δ E ] 补 = [ E x ] 补 + [ − E y ] 补 = 11 , 101 + 00 , 100 = 00 , 001 [\Delta E]_补=[E_x]_补+[-E_y]_补=11,101+00,100=00,001 [ΔE]补=[Ex]补+[−Ey]补=11,101+00,100=00,001
[ Δ E ] 补 > 0 ,应 E y 向 E x 对齐,则 : [\Delta E]_补>0,应E_y向E_x对齐,则: [ΔE]补>0,应Ey向Ex对齐,则:
[ E y ] 补 + 1 = 11 , 100 + 00 , 001 = 11 , 101 [E_y]补+1=11,100+00,001=11,101 [Ey]补+1=11,100+00,001=11,101
[ Δ E ] 补 + [ − 1 ] 补 = 00 , 001 + 11 , 111 = 0 至此, E y = E x ,对毕。 [ΔE]补+[-1]补=00,001+11,111=0\\ 至此, E_y=E_x,对毕。 [ΔE]补+[−1]补=00,001+11,111=0至此,Ey=Ex,对毕。
[ y ] 补 = 11 , 101 ; 11.101100 2 ) 尾数运算 : [y]补=11,101;11.101100\\ 2)尾数运算: [y]补=11,101;11.1011002)尾数运算:
[ M x ] 补 + [ − M y ] 补 = [M_x]_补+[-M_y]_补= [Mx]补+[−My]补=
00.110100 + 00.010100 01.001000 \begin{array}{c} &00.110100 \\ +&00.010100\\ \hline & 01.001000 \\ \end{array} +00.11010000.01010001.001000
3 ) 结果规格化 : 右规 3)结果规格化:右规 3)结果规格化:右规
[ x − y ] 补 = 11 , 101 ; 01.001 000 = 11 , 110 ; 00.100 100 4 ) 舍入 : 不需舍入。 5 ) 溢出 : 无 则 : x − y = 2 − 010 × ( 0.100 100 ) = 2 − 2 × ( 9 / 16 ) [x-y]_补=11,101;01.001\ 000=11,110;00.100\ 100\\ 4)舍入:不需舍入。\\ 5)溢出:无\\ 则:x-y=2^{-010}\times (0.100\ 100)=2^{-2}\times(9/16) [x−y]补=11,101;01.001 000=11,110;00.100 1004)舍入:不需舍入。5)溢出:无则:x−y=2−010×(0.100 100)=2−2×(9/16)
( 3 ) [ 2 3 × ( 13 / 16 ) ] × [ 2 4 × ( − 9 / 16 ) ] x = 2 3 × ( 13 / 16 ) = 2 011 × ( 0.110 100 ) y = 2 4 × ( − 9 / 16 ) = 2 100 × ( − 0.100 100 ) (3)[2^3\times (13/16)]\times [2^4\times (-9/16)] \\ x=2^3\times (13/16)=2^{011}\times (0.110\ 100)\\ y=2^4\times (-9/16)=2^{100}\times (-0.100\ 100) (3)[23×(13/16)]×[24×(−9/16)]x=23×(13/16)=2011×(0.110 100)y=24×(−9/16)=2100×(−0.100 100)
[ x ] 阶补尾补 = 00 , 011 ; 0.110 100 [x]_{阶补尾补}=00,011;0.110\ 100 [x]阶补尾补=00,011;0.110 100
[ y ] 阶补尾补 = 00 , 100 ; 1.011 100 1 ) 阶码相加 : [y]_{阶补尾补}=00,100;1.011\ 100\\ 1)阶码相加: [y]阶补尾补=00,100;1.011 1001)阶码相加:
[ E x ] 补 + [ E y ] 补 = 00 , 011 + 00 , 100 = 00 , 111 ( 无溢出 ) 2 ) 尾数相乘 : [E_x]_补+[E_y]_补=00,011+00,100=00,111(无溢出)\\ 2)尾数相乘: [Ex]补+[Ey]补=00,011+00,100=00,111(无溢出)2)尾数相乘:
补码两位乘比较法:

[ M x × M y ] 补 = 11.100 010 ( 110 000 00 ) 3 ) 结果规格化 : 左规 1 位。 [M_x\times M_y]_补=11.100\ 010(110\ 000\ 00)\\ 3)结果规格化:左规1位。 [Mx×My]补=11.100 010(110 000 00)3)结果规格化:左规1位。
[ x × y ] 补 = 0 , 111 ; 1.100 010 ( 110 000 00 ) = 0 , 110 ; 1.000 101 ( 100 000 0 ) 4 ) 舍入 : 设采用 0 舍 1 入法,应舍 : [x\times y]_补=0,111;1.100\ 010(110\ 000\ 00) =0,110;1.000\ 101(100\ 000\ 0)\\ 4)舍入:设采用0舍1入法,应舍: [x×y]补=0,111;1.100 010(110 000 00)=0,110;1.000 101(100 000 0)4)舍入:设采用0舍1入法,应舍:
[ x × y ] 阶补尾补 = 0 , 110 ; 1.000 101 5 ) 溢出 : 无 x × y = 2110 × ( − 0.111 011 ) = 2 6 × ( − 59 / 64 ) [x\times y]_{阶补尾补}=0,110;1.000\ 101\\ 5)溢出:无\\ x\times y=2{110}\times (-0.111\ 011)=2^6\times (-59/64) [x×y]阶补尾补=0,110;1.000 1015)溢出:无x×y=2110×(−0.111 011)=26×(−59/64)
( 4 ) [ 2 6 × ( − 11 / 16 ) ] ÷ [ 2 3 × ( − 15 / 16 ) ] x = 2 6 × ( − 11 / 16 ) = 2 110 × ( − 0.101 100 ) y = 2 3 × ( − 15 / 16 ) = 2 011 × ( − 0.111 100 ) (4)[2^6\times (-11/16)]\div[2^3\times (-15/16)]\\ x=2^6\times (-11/16)=2^{110}\times (-0.101\ 100) \\ y=2^3\times (-15/16)=2^{011}\times (-0.111\ 100) (4)[26×(−11/16)]÷[23×(−15/16)]x=26×(−11/16)=2110×(−0.101 100)y=23×(−15/16)=2011×(−0.111 100)
[ x ] 阶补尾补 = 00 , 110 ; 1.010 100 [x]_{阶补尾补}=00,110;1.010\ 100 [x]阶补尾补=00,110;1.010 100
[ y ] 阶补尾补 = 00 , 011 ; 1.000 100 1 ) 阶码相减 : [y]_{阶补尾补}=00,011;1.000\ 100\\ 1)阶码相减: [y]阶补尾补=00,011;1.000 1001)阶码相减:
[ E x ] 补 + [ − E y ] 补 = 00 , 110 + 11 , 101 = 00 , 011 ( 无溢出 ) [E_x]_补+[-E_y]_补=00,110+11,101=00,011(无溢出) [Ex]补+[−Ey]补=00,110+11,101=00,011(无溢出)
2 ) 尾数相除 : 2)尾数相除: 2)尾数相除:
补码加减交替除法

[ M x ÷ M y ] 补 = 0.101 111 , [ r ] 补 = 1.001 000 r = − 0.111 000 × 2 − 6 = − 0.000 000 111 000 [M_x\div M_y]_补= 0.101\ 111,[r]_补=1.001\ 000\\ r=-0.111\ 000\times2^{-6} =-0.000\ 000\ 111\ 000 [Mx÷My]补=0.101 111,[r]补=1.001 000r=−0.111 000×2−6=−0.000 000 111 000
28.如何判断定点和浮点补码加减运算结果是否溢出,如何判断原码和补码的定点除法运算结果是否溢出?
答:
有三种判断定点补码加减运算溢出的办法:
(1)采用一位符号位,若两操作数符号相同(减法时减数需每位取反,末位加1),结果的符号又与原操作数符号不同,则为溢出。
(2)采用一位符号位,加法时最高位(符号位)的进位和次高位的进位异或结果为1时,即为溢出。
(3)采用双符号位,当结果的两个符号位不同时,即为溢出。此时最高位符号位代表真正的符号。
对于浮点补码加减运算要根据运算结果的阶码来判断是否溢出。当阶码大于最大正阶码时为溢出(即:阶码 [ j ] 补 = 01 , × × ⋅ ⋅ ⋅ × × [j]_补=01,\times \times ···\times \times [j]补=01,××⋅⋅⋅××为上溢),此时需中断处理;当阶码小于最小负阶码时(即:阶码 [ j ] 补 = 10 , × × ⋅ ⋅ ⋅ × × [j]_补=10,\times \times ···\times \times [j]补=10,××⋅⋅⋅××,按机器零处理),按机器零处理。
以小数为例,补码除法第一次即为商符,若商符与两操作数符号位异或结果不同,即为溢出。如果两操作数符号相同,第一次上商为1即为溢出;若两操作数符号不同,第一次上商若为0,即为溢出。
浮点数补码除法运算不能以尾数相除结果溢出为判断依据,因为尾数溢出可通过右规校正。仅当最后结果的浮点数阶码大于最大正阶码时,才为真正溢出。
29.设浮点数阶码取3位,尾数取6位(均不包括符号位),要求阶码用移码运算,尾数用补码运算,计算x·y,且结果保留1倍字长。
( 1 ) x = 2 − 100 × 0101101 , y = 2 − 011 × ( − 0110101 ) ; ( 2 ) x = 2 − 011 × ( − 0.100111 ) , y = 2 101 × ( − 0.101011 ) 。 (1)x=2^{-100}\times 0101101,y=2^{-011}\times (-0110101);\\ (2) x=2^{-011}\times (-0.100111),y=2^{101}\times (-0.101011)。 (1)x=2−100×0101101,y=2−011×(−0110101);(2)x=2−011×(−0.100111),y=2101×(−0.101011)。
答:
先将 x 、 y 转换成机器数形式 : ( 1 ) [ x ] 阶移尾补 = 0 , 100 ; 0.101 101 先将x、y转换成机器数形式:\\ (1)[x]_{阶移尾补}=0,100;0.101\ 101 先将x、y转换成机器数形式:(1)[x]阶移尾补=0,100;0.101 101
[ y ] 阶移尾补 = 0 , 101 ; 1.001 011 1 ) 阶码相加 : [y]_{阶移尾补}=0,101;1.001\ 011\\ 1)阶码相加: [y]阶移尾补=0,101;1.001 0111)阶码相加:
[ E x ] 移 + [ E y ] 补 = 00 , 100 + 11 , 101 = 00 , 001 ( 无溢出 ) [E_x]_移+[E_y]_补=00,100+11,101=00,001(无溢出) [Ex]移+[Ey]补=00,100+11,101=00,001(无溢出)
2 ) 尾数相乘 : 2)尾数相乘: 2)尾数相乘:
算法一:补码两位乘比较法

[ M x × M y ] 补 = 1.011 010 ( 101 111 00 ) 3 ) 结果规格化 : 已是规格化数。 4 ) 舍入 : 设采用 0 舍 1 入法,应入 : [M_x\times M_y]_补=1.011\ 010(101\ 111\ 00)\\ 3)结果规格化:已是规格化数。\\ 4)舍入:设采用0舍1入法,应入: [Mx×My]补=1.011 010(101 111 00)3)结果规格化:已是规格化数。4)舍入:设采用0舍1入法,应入:
[ x × y ] 阶移尾补 = 0 , 001 ; 1.011 011 5 ) 溢出 : 无 x × y = 2 − 111 × ( − 0.100 101 ) [x\times y]_{阶移尾补}=0,001;1.011\ 011\\ 5)溢出:无\\ x\times y=2^{-111}\times (-0.100\ 101) [x×y]阶移尾补=0,001;1.011 0115)溢出:无x×y=2−111×(−0.100 101)
( 2 ) x = 2 − 011 × ( − 0.100 111 ) y = 2 101 × ( − 0.101 011 ) (2)x=2^{-011}\times (-0.100\ 111)\\ y=2^{101}\times (-0.101\ 011) (2)x=2−011×(−0.100 111)y=2101×(−0.101 011)
[ x ] 阶移尾补 = 0 , 101 ; 1.011 001 [x]_{阶移尾补}=0,101;1.011\ 001 [x]阶移尾补=0,101;1.011 001
[ y ] 阶移尾补 = 1 , 101 ; 1.010 101 1 ) 阶码相加 : [y]_{阶移尾补}=1,101;1.010\ 101\\ 1)阶码相加: [y]阶移尾补=1,101;1.010 1011)阶码相加:
[ E x ] 移 + [ E y ] 补 = 00 , 101 + 00 , 101 = 01 , 010 ( 无溢出 ) [E_x]_移+[E_y]_补=00,101+00,101 =01,010(无溢出) [Ex]移+[Ey]补=00,101+00,101=01,010(无溢出)
2 ) 尾数相乘 : 2)尾数相乘: 2)尾数相乘:
算法一:补码两位乘比较法

[ M x × M y ] 补 = 0.011 010 ( 001 101 00 ) [M_x\times M_y]_补=0.011\ 010(001\ 101\ 00) [Mx×My]补=0.011 010(001 101 00)
2 ) 尾数相乘 : 2)尾数相乘: 2)尾数相乘:
算法二:补码一位乘比较法

[ M x × M y ] 补 = 0.011 010 ( 001 101 0 ) [M_x\times M_y]_补=0.011\ 010(001\ 101\ 0) [Mx×My]补=0.011 010(001 101 0)
3 ) 结果规格化 : 3)结果规格化: 3)结果规格化:
[ x × y ] 阶移尾补 = 1 , 010 ; 0.011 010 ( 001 101 00 ) = 1 , 001 ; . 0.110 100 ( 011 010 0 ) ( 左规 1 次,阶码减 1 ,尾数左移 1 位 ) 4 ) 舍入 : 设采用 0 舍 1 入法,应舍 : [x\times y]_{阶移尾补}=1,010;0.011\ 010(001\ 101\ 00)=1,001;.0.110\ 100(011\ 010\ 0)\\ (左规1次,阶码减1,尾数左移1位)\\ 4)舍入:设采用0舍1入法,应舍: [x×y]阶移尾补=1,010;0.011 010(001 101 00)=1,001;.0.110 100(011 010 0)(左规1次,阶码减1,尾数左移1位)4)舍入:设采用0舍1入法,应舍:
[ x × y ] 阶移尾补 = 1 , 001 ; 0.110 100 5 ) 溢出 : 无 x × y = 2 001 × 0.110 100 [x\times y]_{阶移尾补}=1,001;0.110\ 100\\ 5)溢出:无\\ x\times y=2^{001}\times 0.110\ 100 [x×y]阶移尾补=1,001;0.110 1005)溢出:无x×y=2001×0.110 100
注意:采用阶移尾补格式是指:参加运算的数是阶移尾补格式,用阶移尾补算法计算,运算结果是阶移尾补格式。
30.机器数格式同上题,要求阶码用移码运算,尾数用补码运算,计算 x ÷ y x\div y x÷y。(注:改用阶移尾原格式作。)
( 1 ) x = 2 101 × 0.100111 , y = 2 011 × ( − 0.101011 ) ; ( 2 ) x = 2 110 × ( − 0.101101 ) , y = 2 011 × ( − 0.111100 ) 。 (1)x=2^{101}\times 0.100111, y=2^{011}\times (-0.101011);\\ (2)x=2^{110}\times (-0.101101), y=2^{011}\times (-0.111100)。 (1)x=2101×0.100111,y=2011×(−0.101011);(2)x=2110×(−0.101101),y=2011×(−0.111100)。
答:
先将 x 、 y 转换成机器数形式 : ( 1 ) [ x ] 阶移尾原 = 1 , 101 ; 0.100 111 先将x、y转换成机器数形式:\\ (1)[x]_{阶移尾原}=1,101;0.100\ 111 先将x、y转换成机器数形式:(1)[x]阶移尾原=1,101;0.100 111
[ y ] 阶移尾原 = 1 , 011 ; 1.101 011 1 ) 阶码相减 : [y]_{阶移尾原}=1,011;1.101\ 011\\ 1)阶码相减: [y]阶移尾原=1,011;1.101 0111)阶码相减:
[ E x ] 移 + [ − E y ] 补 = 01 , 101 + 11 , 101 = 01 , 010 ( 无溢出 ) [E_x]_移+[-E_y]_补=01,101+11,101 =01,010(无溢出) [Ex]移+[−Ey]补=01,101+11,101=01,010(无溢出)
2 ) 尾数相除 : ( 原码加减交替除法 ) 2)尾数相除:(原码加减交替除法) 2)尾数相除:(原码加减交替除法)

M x ∗ ÷ M y ∗ = 0.111 010 , [ M x ÷ M y ] 原 = 1.111 010 r ∗ = 0.000 010 × 2 − 6 = 0.000 000 000 010 M_{x}^*\div M_{y}^*= 0.111\ 010 ,[M_x\div M_y]_原= 1.111\ 010\\ r^*= 0.000\ 010\times2^{-6}= 0.000\ 000\ 000\ 010 Mx∗÷My∗=0.111 010,[Mx÷My]原=1.111 010r∗=0.000 010×2−6=0.000 000 000 010
3 ) 结果规格化 : 已是规格化数。 4 ) 舍入 : 已截断法舍入。 5 ) 溢出 : 无 3)结果规格化:已是规格化数。\\ 4)舍入:已截断法舍入。\\ 5)溢出:无 3)结果规格化:已是规格化数。4)舍入:已截断法舍入。5)溢出:无
[ x ÷ y ] 阶移尾原 = 1 , 010 ; 1.111 010 x ÷ y = 2 010 × ( − 0.111 010 ) [x\div y]_{阶移尾原}=1,010;1.111\ 010 \\ x\div y=2^{010}\times (-0.111\ 010) [x÷y]阶移尾原=1,010;1.111 010x÷y=2010×(−0.111 010)
( 2 ) x = 2 110 × ( − 010 1101 ) y = 2 011 × ( − 0111 100 ) (2)x=2^{110}\times(-010\ 1101)\\ y=2^{011}\times(-0111\ 100) (2)x=2110×(−010 1101)y=2011×(−0111 100)
[ x ] 阶移尾原 = 1 , 110 ; 1.101 101 [x]_{阶移尾原}=1,110;1.101\ 101 [x]阶移尾原=1,110;1.101 101
[ y ] 阶移尾原 = 1 , 011 ; 1.111 100 1 ) 阶码相减 : [y]_{阶移尾原}=1,011;1.111\ 100\\ 1)阶码相减: [y]阶移尾原=1,011;1.111 1001)阶码相减:
[ E x ] 移 + [ − E y ] 补 = 01 , 110 + 11 , 101 = 01 , 011 ( 无溢出 ) [E_x]_移+[-E_y]_补=01,110+11,101=01,011(无溢出) [Ex]移+[−Ey]补=01,110+11,101=01,011(无溢出)
2 ) 尾数相除 : ( 原码加减交替除法 ) 2)尾数相除:(原码加减交替除法) 2)尾数相除:(原码加减交替除法)

M x ∗ ÷ M y ∗ = [ M x ÷ M y ] 原 = 0.110 000 r ∗ = − 0.000 000 × 2 − 6 = − 0.000 000 000 000 M_{x}^*\div M_{y}^*= [M_x\div M_y]_原= 0.110\ 000\\ r^*=-0.000\ 000 \times 2^{-6}=-0.000\ 000\ 000\ 000 Mx∗÷My∗=[Mx÷My]原=0.110 000r∗=−0.000 000×2−6=−0.000 000 000 000
注:由于加减交替除法算法中缺少对部分余数判“0”的步骤,因此算法运行中的某一步已除尽时,算法不会自动停止,而是继续按既定步数运行完。
3 ) 结果规格化 : 已是规格化数。 4 ) 舍入 : 已截断法舍入。 5 ) 溢出 : 无 3)结果规格化:已是规格化数。\\ 4)舍入:已截断法舍入。\\ 5)溢出:无 3)结果规格化:已是规格化数。4)舍入:已截断法舍入。5)溢出:无
[ x ÷ y ] 阶移尾原 = 1 , 011 ; 0.110 000 x ÷ y = 2 011 × 0.110 000 [x\div y]_{阶移尾原}=1,011;0.110\ 000 \\ x\div y=2^{011}\times 0.110\ 000 [x÷y]阶移尾原=1,011;0.110 000x÷y=2011×0.110 000
31.设机器字长为32位,用与非门和与或非门设计一个并行加法器(假设与非门的延迟时间为30ns,与或非门的延迟时间为45ns),要求完成32位加法时间不得超过0.6 μ s \mu s μs。画出进位链及加法器逻辑框图。
答:
首先根据题意要求选择进位方案:
1)若采用串行进位链(行波进位),则在 d i 、 t i d_i、t_i di、ti函数的基础上,实现32位进位需要的时间为:
T = 2 t y × 32 = 64 t y = 64 × 30 = 1920 n s T=2t_y\times 32=64t_y=64\times 30=1920ns T=2ty×32=64ty=64×30=1920ns
不满足 0.6 μ s 0.6\mu s 0.6μs的加法时间限制,不能用。(设 1 t y = 30 n s 1t_y=30ns 1ty=30ns)
2)若采用单重分组跳跃进位(级连方式),则在di、ti的基础上,4位一组分组,32位进位需:
T = 2.5 t y × 8 组 = 20 t y = 20 × 30 = 600 n s T=2.5t_y\times 8组=20t_y=20\times 30=600ns T=2.5ty×8组=20ty=20×30=600ns
刚好满足 0.6 μ s 0.6\mu s 0.6μs加法时间的限制。
考虑到一次加法除进位时间外,还需di、 ti函数的产生时间、和的产生时间(最高位和)等因素,故此进位方案仍不适用。
结论:若采用单重分组跳跃进位,小组规模需在6位以上较为合适。即:
T = 2.5 t y × 6 组 = 15 t y = 15 × 30 = 450 n s T=2.5t_y\times 6组=15t_y=15\times 30=450ns T=2.5ty×6组=15ty=15×30=450ns
除进位外还有 150 n s ( 约 5 t y ) 150ns(约5t_y) 150ns(约5ty)左右的时间供加法开销,较充裕。
3)若采用双重分组跳跃进位(二级先行-级联进位),4位一小组,4小组为一大组分组,则32位进位需:
T = 2.5 t y × 4 级 = 10 t y = 10 × 30 = 300 n s T=2.5t_y\times 4级=10t_y=10\times 30=300ns T=2.5ty×4级=10ty=10×30=300ns
完全满足 0.6 μ s 0.6\mu s 0.6μs的加法时间限制,可以使用。
双重分组跳跃进位(两级先行进位)
32位双重分组跳跃进位的进位链框图见教材286页图6.23。

6位一组单重分组跳跃进位的进位链框图如下:

注:一个完整的加法器还应考虑 d i 、 t i d_i、t_i di、ti产生电路、求和电路等。
加法器逻辑框图如下。图中,进位链电路可选上述两种方案之一。

32.设机器字长为16位,分别按4、4、4、4和5、5、3、3分组后
(1)画出两种分组方案的单重分组并行进位链框图,并比较哪种方案运算速度快。
(2)画出两种分组方案的双重分组并行进位链框图,并对这两种方案进行比较。
(3)用74181和74182画出单重和双重分组的并行进位链框图。
答:
(1)4-4-4-4分组的16位单重分组并行进位链框图见教材286页图6.22。
单重分组跳跃进位(一级先行进位)
16位并行加法器进位链框图(6.22)

注意:16位一级先行进位加法器最长进位延迟时间为 10 t y 10t_y 10ty。
5-5-3-3分组的16位单重分组并行进位链框图如下:

4-4-4-4分组的进位时间 = 2.5 t y × 4 = 10 t y ; =2.5t_y\times 4=10t_y; =2.5ty×4=10ty;
5-5-3-3分组的进位时间 = 2.5 t y × 4 = 10 t y ; =2.5t_y\times 4=10t_y; =2.5ty×4=10ty;
两种分组方案最长加法时间相同。
结论:单重分组并行进位的最长进位时间只与组数有关,与组内位数无关。
(2)4-4-4-4分组的16位双重分组并行进位链框图见教材288页图6.26。

5-5-3-3分组的16位双重分组并行进位链框图如下:

4-4-4-4分组的进位时间 = 2.5 t y × 3 = 7.5 t y ; =2.5t_y\times 3=7.5t_y; =2.5ty×3=7.5ty;
5-5-3-3分组的进位时间 = 2.5 t y × 3 = 7.5 t y ; =2.5t_y\times 3=7.5t_y; =2.5ty×3=7.5ty;
两种分组方案最长加法时间相同。
结论:双重分组并行进位的最长进位时间只与组数和级数有关,与组内位数无关。
(3)单重分组16位并行加法器逻辑图如下(正逻辑):

双重分组16位并行加法器逻辑图如下(正逻辑):

图中,设与进位无关的引脚省略不画,不用的引脚也省略不画。
注意:
1)181芯片正、负逻辑的引脚表示方法;
2)为强调可比性,5-5-3-3分组时不考虑扇入影响;
3)181芯片只有最高、最低两个进位输入/输出端组内进位无引脚;
4)181为4位片,无法5-5-3-3分组,只能4-4-4-4分组;
5)单重分组跳跃进位只用到181,使用182的一般是双重以上分组跳跃进位;
6)单重分组跳跃进位是并行进位和串行进位技术的结合;双重分组跳跃进位是二级并行进位技术;特别注意在位数较少时,双重分组跳跃进位可以采用全先行进位技术实现;位数较多时,可采用双重分组跳跃进位和串行进位技术结合实现。