Y:“此题有蓝桥杯A组国赛的难度 或 ACM银牌的难度”
研究了两个下午终于把细节想清楚
题目描述:
定一个长度为 N 的序列 A ,要求把该序列分成若干段,在满足“每段中所有数的和”不超过 M 的前提下,让“每段中所有数的最大值”之和最小。 试计算这个最小值。
输入格式 第一行包含两个整数 N 和 M 。 第二行包含 N 个整数,表示完整的序列 A 。
输出格式 输出一个整数,表示结果。 如果结果不存在,则输出 −1 。
数据范围 0≤N≤105 , 0≤M≤1011 , 序列A中的数非负,且不超过106
输入样例: 8 17 2 2 2 8 1 8 2 1
输出样例: 12
N 的范围是 1E5 时间复杂度应该控制在O(NlogN)级别
暴力枚举 三重循环 时间复杂度O(N^3) 级别
远远大于 10^8 考虑如何优化
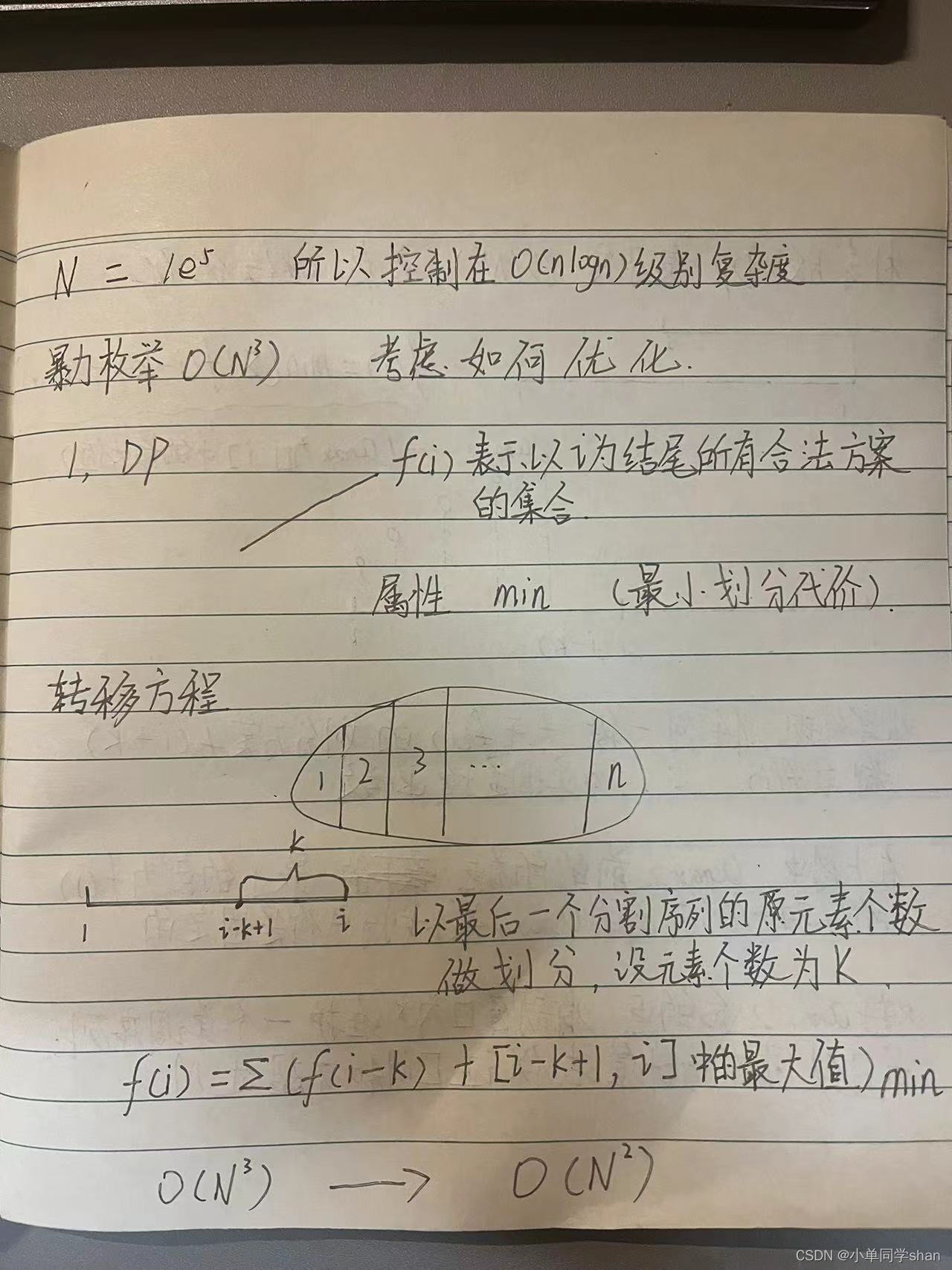
1,DP
状态定义:
f(i):表示所有以i结尾合法划分方案的集合
属性:最小划分代价
状态转移 :
以最后一个分割序列的元素个数做划分,假设最后一个分割序列的元素个数是k
那么有 f(i) = min(Σ(f(i - k) + amax)); 注:amax表示最后一个分割序列中最大的数
2.双指针 + 单调队列

如上图所示,观察发现,对于任何一段大于f(i)的划分方案,都可以在f(i) 中找到一种划分方案与之对应,并且划分代价严格 >= f(i),所以f(i)为单调递增函数
因为f是单调递增的,所以对于最后一个区间内的最大值amax,当最后一个区间的左端点j在此时的amax左边时,我们只需要考虑一个点用来转移就可以:一个最靠左边的点。
这样在非最坏情况下,就不需要枚举每一个k来进行状态计算,而是枚举每一个可用的区间最大值。
当区间左端点J到达当前的amax时,f(j)的含义是——以J为结尾的划分方案
那转移的时候,由于我们的转移方程为——f(j)+ 最后一段的划分代价amax,那么amax不在作为最后一段的划分代价更新,此时需要重新再找一个amax
根据这个性质,所以可以想到用单调队列来维护一个滑动窗口单调序列
则队头就是一个当前可用的amax.当左端点J超过amax的时候,弹出这个元素,下一个元素仍然是当前可用的区间最大值。
注:这是单调队列维护滑动窗口最值问题,队列中维护的是(最大值,次大值,次次大值....) 这里不做过多赘
双指针算法则可以保证区间和不超过m
但此时的我们的时间复杂度最坏情况下仍然是O(N^2)
因为最坏情况下,仍然可能存在n个元素单调序列,对于每个滑动窗口,都需要枚举单调队列中的每个点来更新最小值,考虑如何继续优化。
现在来回顾一下我们做了什么:
DP状态转移方程推出以后,对于每一个f(i),在转移的时候都需要枚举——所有的 最后一个合法划分方案 的 元素个数K 此算法的时间复杂度在O(N^2)以上
由于f(i)是单调递增函数,所以对于每一个可用的amax,都只需要考虑最小的那个点即可
所以想到用单调队列维护一个滑动窗口最值,队头即是当前可用的最大值amax。
但最坏情况下,仍然可能存在n个单调序列,这种情况下,等价于没有优化。
3.multiset
那此时我们的需求就变成了,维护一个区间内的最小值,用于状态计算。
如果可以动态维护出这个集合中的最小值,转移的时候就不需要枚举每一个amax了。
动态维护一个区间内的最小值,很多数据结构都可以实现。比如:堆,平衡树
可以直接用STL中的 set 来维护(平衡树实现),并且和滑动窗口同步,每次最多增加一个元素,删除一个元素,复杂度是O(log)级别;
这样即使是最坏情况下,我们也不需要枚举每一个可能的amax(最多为n),
这样就从O(N^2)优化到了O(NlogN);
能坚持看到这里,给你点赞!
代码实现:
#include<iostream>
#include<cstdio>
#include<cstring>
#include<set>
using namespace std;
const int N = 1e5 + 10;
typedef long long LL;
LL f[N];
int q[N];
LL a[N];
int n;
LL m;
multiset<LL> s;
void remove(LL k)//这样写的目的是维护集合中,防止把多个相同值都删掉
{
auto x = s.find(k);
s.erase(x);//用迭代器只删除当前位置
}
int main()
{
cin >> n >> m;
for(int i = 1; i <= n; i ++ )
{
cin >> a[i];
if(a[i] > m) //出现大于m的值,一定不存在合法划分方案
{
puts("-1");
return 0;
}
}
int hh = 0,tt = -1;
LL sum = 0;
for(int i = 1, j = 1; i <= n; i ++)//双指针维护区间不超过m的滑动窗口
{
sum += a[i];
while(sum > m)
{
sum -= a[j ++ ];//j为左端点
if(hh <= tt && q[hh] < j)//如果队列中最左边的位置小于滑动窗口左端点 删除掉
{
if(hh < tt) remove(f[q[hh]] + a[q[hh + 1]]);
hh ++;
}
}
while(hh <= tt && a[q[tt]] <= a[i])
/*单调队列 如果队尾元素小于等于当前元素 一定不会作为最大值更新,删除掉*/
{
if(hh < tt) remove(f[q[tt - 1]] + a[q[tt]]);
tt --;
}
q[ ++ tt ] = i;//队尾加入当前元素
if(hh < tt) s.insert(f[q[tt - 1]] + a[q[tt]]);//hh < tt 保证队列中至少两个点
f[i] = f[j - 1] + a[q[hh]];
/*注意:j是区间左端点,包括在最后一个区间内的,计算的时候需要-1才是上一个区间,否则的话不符合转移方程.这一步是以第一个amax也就是单调队列中的第一个元素来计算f(i),set中维护的是从第二个amax作为最后一段最大值开始的,这步我想了很久才想通,特别注意下*/
if(s.size()) f[i] = min(f[i],*s.begin());
}
printf("%lld", f[n]);
return 0;
}
tip:
j是双指针维护的区间左端点,所以是包括在最后一个区间内的,
那么状态转移的时候需要 -1 才是上一个区间的末尾位置,否则的话不符合转移方程.
set中维护的是从 以 第二个amax作为最后一段的最大值 开始的 之后的 情况
第一个amax是作为第二个amax所对应的最小 f() 来计算的,因为f单调
也就是说,每一个可能的amax所对应的最小 f()就在 上一个amax的位置上
f(上一个amax的位置) 表示以 上一个amax的位置为结尾的 所有划分方案的集合
那么最后一段的划分方案中就不能使用这个值作为最大值了
这步我想了很久才想通,特别注意下!
