点分治简述

点分治通常用于求解树上路径问题。点分治可以认为是一种暴力思想，结合了树的重心优化了搜索的结构，通常对于一个点求解之后，考虑每一个子树时，抽象地将子树和这个节点分离，然后通过递归这些子树的重心，来优化搜索的层数，以优化时间复杂度。

LuoguP3806 - 【模板】点分治1

通过这道模板题来具体描述点分治的实现过程。

题目给了一棵带边权的树，进行多次查询，每次查询这棵树上长度为 $k$ 的路径是否存在。

问题简化

先考虑这个问题：给一棵带边权的树，查询最高点为 $u$ 点的路径中是否有长度为 $k$ 的路径。

不难想到，我们可以考虑所有子树中的点，dfs求一下从这个点到这些点的距离，将他们按照距离从小到大排序。然后用双指针，一个指针初始指向最左端，即离 $u$ 最近的点，另一个指针初始指向最右端，即离 $u$ 最远的点。我们看左右指针所指的点所形成的路径长度是否为 $k$ 。如果是 $k$ ，则说明存在路径，结束搜索，继续移动指针。左指针每向右移动而导致当前所指的点离 $u$ 的距离变大时，相应的，右指针也要向左移动，令其所指的点离 $u$ 的距离变小，才有可能继续维持在 $k$ 的长度。

这里要考虑一个问题，那就是这两个节点的最近公共祖先可能是 $u$ 的子节点，即选出的点可能是这个样子：

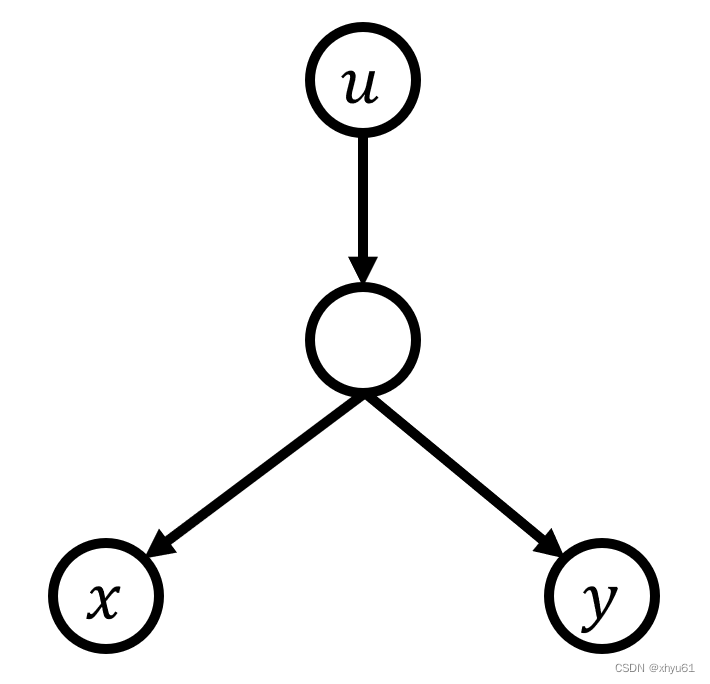
在这里插入图片描述
其中， $x, y$ 到 $u$ 点的距离之和为 $k$ 。然而这种情况不属于一条路径，所以我们需要将这种情况判出来，要保证我们判定距离 $k$ 的路径存在，必须满足这两个点从属于 $u$ 的不同子树。

具体的方法是，我们会通过一次dfs将 $u$ 的所有子树中的点到 $u$ 的距离求出，于此同时，我们也可以在这次dfs中把所有的点从属于 $u$ 的哪一个子树标记出来（标记为这棵子树的根节点，即 $u$ 的某一个儿子）。这样的话，如果当前两个指针所指向的点如果从属于同一个子树，那么直接跳过这种情况。

回归原题

对于一个节点 $x$ ，我们可以将所有的路径分为最高点（离根节点最近）为 $x$ 的路径和最高点不是 $x$ 的路径。也就是说对于每一个节点，我们只需要考虑以这个节点为最高点的路径即可。

点分治做法暴力探讨每一个点 $u$ ，查看每一个以 $u$ 为最高点的路径，看是否有长度为 $k$ 的路径。

在具体介绍点分治做法前，先介绍树的重心。树的重心是指一棵树的所有节点包含的子树中最大的子树最小的节点。

一棵树的重心可以通过对这棵树的一次dfs来求解：首先在整个dfs中明确这棵树的大小，设为 $T ree S i ze$ 。在dfs的过程中维护每一个节点 $u$ 所在的子树的大小，设为 $sz [u]$ 。那么这个节点包含的所有子树的最大子树值，就是它所有的子节点为根节点的子树和父节点那一侧的子树（大小为 $T ree S i ze - sz [u]$ ）中最大的那个。我们从下往上不断寻找这个值最小的那个节点就是这棵树的重心。

点分治的主体仍然是dfs，每次dfs到的节点的处理方式和上述的相同。只不过点分治对整个dfs的优化的点在于，每次查询完一个点之后往下dfs并不按照原有的树的结构进行dfs。考虑到我们的分类方式，我们对每一个点的操作只考虑这个点为最高点的路径，不会再考虑上面的树的点了，所以可以直接抽象地将这个子树和下面的树分隔开，下一次dfs直接dfs到这个点的子树的重心上去，然后强制让这个重心变成根节点，这样这棵子树的层数就变得很平均，递归的次数就会变得很少，可以减少非常多的时间。

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 10005;

int n, m, k, en, root, tot;
int front[N], q[10000005], sz[N], mx[N], vis[N], ok[105];
int dis[N], bel[N], a[N];

struct Edge {
    
    
	int v, w, next;
}e[N * 2];

void addEdge(int u, int v, int w) {
    
    
	e[++en] = {
    
    v, w, front[u]};
	front[u] = en;
}

void get_root(int u, int f, int total) {
    
    
	sz[u] = 1;
	mx[u] = 0;
	for (int i = front[u]; i; i = e[i].next) {
    
    
		int v = e[i].v;
		if (v == f or vis[v]) continue;
		//vis[v]=1说明这个点已经计算过
		//当前结构下v的子树全部是已经计算过的点，所以可以直接抽象分割
		get_root(v, u, total);
		sz[u] += sz[v];
		mx[u] = max(mx[u], sz[v]);//求最大子树的大小
	}
	mx[u] = max(mx[u], total - sz[u]);//考虑父节点一侧的子树大小
	if (!root or mx[u] < mx[root]) {
    
    
		root = u;
	}
}

void get_dis(int u, int f, int d, int subroot) {
    
    
	//subroot表示当前的节点从属于当前计算的节点的哪一个子节点
	a[++tot] = u;
	dis[u] = d;//标记这个点离当前计算的点的距离
	bel[u] = subroot;//标记这个点从属于当前计算的节点的哪一个子节点
	for (int i = front[u]; i; i = e[i].next) {
    
    
		int v = e[i].v, w = e[i].w;
		if (v == f or vis[v]) continue;
		get_dis(v, u, d + w, subroot);
	}
}

void calc(int u) {
    
    
	tot = 0;
	a[++tot] = u;
	dis[u] = 0; bel[u] = u;
	//不要忘记把自己加进去
	//可以利用自己这个节点统计到自己既是最高点又是路径一端的路径
	for (int i = front[u]; i; i = e[i].next) {
    
    
		int v = e[i].v, w = e[i].w;
		if (vis[v]) continue;
		get_dis(v, u, w, v);
	}
	sort(a + 1, a + tot + 1, [](const int &A, const int &B) {
    
    
		return dis[A] < dis[B];//将所有点按照到这个点的距离从小到大排序
	});
	for (int i = 1; i <= m; ++i) {
    
    
		int l = 1, r = tot;
		if (ok[i]) continue;
		while (l < r) {
    
    
			if (dis[a[l]] + dis[a[r]] > q[i]) --r;
			else if (dis[a[l]] + dis[a[r]] < q[i]) ++l;
			else if (bel[a[l]] == bel[a[r]]) {
    
    
				//从属于u的同一个子节点，继续移动指针
				if (dis[a[r]] == dis[a[r - 1]]) --r;
				else ++l;
			}
			else {
    
    
				ok[i] = 1;
				break;
			}
		}
	}
}

void get_ans(int u) {
    
    
	vis[u] = 1;
	calc(u);
	for (int i = front[u]; i; i = e[i].next) {
    
    
		int v = e[i].v, w = e[i].w;
		if (vis[v]) continue;
		root = 0;
		get_root(v, 0, sz[v]);
		get_ans(root);
	}
}

void main2() {
    
    
	cin >> n >> m;
	en = 0;
	for (int i = 1; i <= n; ++i) {
    
    
		front[i] = 0;
	}
	for (int i = 1; i <= n - 1; ++i) {
    
    
		int u, v, w;
		cin >> u >> v >> w;
		addEdge(u, v, w);
		addEdge(v, u, w);
	}
	for (int i = 1; i <= m; ++i) {
    
    
		ok[i] = 0;//离线来做，对所有的询问用1个dfs统一查询
	}
	for (int i = 1; i <= m; ++i) {
    
    
		cin >> q[i];
		if (!q[i]) ok[i] = 1; //询问可能是0，进行特判
	}
	mx[0] = n;
	get_root(1, 0, n);
	get_ans(root);
	for (int i = 1; i <= m; ++i) {
    
    
		if (ok[i]) cout << "AYE\n";
		else cout << "NAY\n";
	}
}

int main() {
    
    
	ios::sync_with_stdio(false);
	cin.tie(0); cout.tie(0);
	LL _ = 1;
//	cin >> _;
	while (_--) main2();
	return 0;
}

POJ1741 - Tree

题目链接

（双倍经验题目：LuoguP4178 - Tree）

和刚才的询问不同的是，这个题查询所有长度小于等于 $k$ 的路径数量。

整体点分治框架和上一题一样，唯一不同的就是如何统计答案。

考虑一棵树的一个点及其所有子树。我们想求以这个点为最高点的所有长度不超过 $k$ 的路径总和。

我们同样对于每一个点，把它所有的子树中的点全部摘出来，然后按照到这个点的距离从小到大进行排序。排序后，依旧设置一对左右指针，这个左右指针所指的两个点到 $u$ 的路径之和满足是最大可能的不超过 $k$ 的一对。然后对于左指针的点来说，一共有 $r - l + 1$ 条路径符合答案，其中右指针所指的是第 $r$ 个点，左指针指的是第 $l$ 个点。和上一道题一样，存在两个点取在同一个 $u$ 的子树之下。这个时候不能像上一道题那样通过判断来实现，因为我们不再是一个点一个点看了，而是直接统计一段的数量。

我们这道题目可以结合容斥的思想，考虑每一个子节点中符合条件的两个点的贡献算出来，从答案中减去即可。

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cstdlib>
#include<cmath>
using namespace std;
typedef long long LL;
const int N = 10005;

int n, k, en, root, tot;
int front[N], sz[N], mxp[N];
int a[N], dis[N], bel[N], vis[N];
LL ans;

struct Edge {
    
    
	int v, w, next;
}e[N * 2];

void addEdge(int u, int v, int w) {
    
    
	++en;
	e[en].v = v;
	e[en].w = w;
	e[en].next = front[u];
	front[u] = en;
}

void get_root(int u, int f, int total) {
    
    
	sz[u] = 1;
	mxp[u] = 0;
	for (int i = front[u]; i; i = e[i].next) {
    
    
		int v = e[i].v, w = e[i].w;
		if (v == f or vis[v]) continue;
		get_root(v, u, total);
		sz[u] += sz[v];
		mxp[u] = max(mxp[u], sz[v]);
	}
	mxp[u] = max(mxp[u], total - sz[u]);
	if (!root or mxp[u] < mxp[root]) {
    
    
		root = u;
	}
}

void get_dis(int u, int f, int d, int subroot) {
    
    
	a[++tot] = u;
	dis[u] = d;
	bel[u] = subroot;
	for (int i = front[u]; i; i = e[i].next) {
    
    
		int v = e[i].v, w = e[i].w;
		if (v == f or vis[v]) continue;
		get_dis(v, u, d + w, subroot);
	}
}

bool cmp(const int &A, const int &B) {
    
    
	return dis[A] < dis[B];
}

//minus是判别当前计算的答案是加到答案里还是从答案中抠去
void calc(int u, int ori, bool minus) {
    
    
	tot = 0;
	a[++tot] = u;
	dis[u] = ori;
	bel[u] = u;
	for (int i = front[u]; i; i = e[i].next) {
    
    
		int v = e[i].v, w = e[i].w;
		if (vis[v]) continue;
		get_dis(v, u, ori + w, v);
		//查询一个点的子节点的时候也要把到子节点的那条边权也算进来
		//ori就是那个边权
	}
	sort(a + 1, a + tot + 1, cmp);
	LL tmp = 0;
	int l = 1, r = tot;
	while (l <= r) {
    
    
		while (r > 0 and dis[a[l]] + dis[a[r]] > k) {
    
    
			--r;
		}
		if (l <= r) {
    
    
			tmp += r - l + 1;
			++l;
		}
		else break;
	}
	if (minus == false) ans += tmp;
	else ans -= tmp;
}

void get_ans(int u) {
    
    
	vis[u] = 1;
	calc(u, 0, false);
	for (int i = front[u]; i; i = e[i].next) {
    
    
		int v = e[i].v, w = e[i].w;
		if (vis[v]) continue;
		calc(v, w, true);//抠出不正确的答案
		root = 0;
		get_root(v, 0, sz[v]);
		get_ans(root);
	}
}

void main2() {
    
    
	en = ans = 0;
	for (int i = 1; i <= n; ++i) {
    
    
		front[i] = vis[i] = 0;
	}
	for (int i = 1; i < n; ++i) {
    
    
		int u, v, w;
		cin >> u >> v >> w;
		addEdge(u, v, w);
		addEdge(v, u, w);
	}
	root = 0;
	mxp[0] = n;
	get_root(1, 0, n);
	get_ans(root);
	cout << ans - n << '\n';
}

int main() {
    
    
//	freopen("Fin.in", "r", stdin);
	ios::sync_with_stdio(false);
	cin.tie(0); cout.tie(0);
	while (1) {
    
    
		cin >> n >> k;
		if (!n and !k) break;
		main2();
	}
	return 0;
}

【做题笔记】点分治

点分治简述

LuoguP3806 - 【模板】点分治1

问题简化

回归原题

POJ1741 - Tree

猜你喜欢