如何用MD5和SHA等构造密码方案中的哈希函数

常见符号

先复习一些常见符号

符号	意义
$p,q$	大素数
${\mathbb{Z}}_p$	集合 { 0 , 1 , 2 , … , p − 1 } \{ 0,1,2, \dots, p-1 \} { 0,1,2,…,p−1}
${\mathbb{Z}}_N^{\ast }$	与$N$互质的整数
${\mathbb{Z}}_p^{\ast }$	与$p$互质的整数，即集合 { 1 , … , p − 1 } \{1, \dots, p-1\} { 1,…,p−1}
{ 0 , 1 } λ \{0, 1\}^\lambda { 0,1}λ	长度为$\lambda$的比特串
{ 0 , 1 } ∗ \{0, 1\}^* { 0,1}∗	任意长度的比特串
$\mathbb{G}$	阶为素数的有限循环群
$\mathbb{G}$	双线性配对有关的有限循环群

如何实现 H : { 0 , 1 } ∗ → Z p ∗ H : \{0, 1\}^* \to \mathbb{Z}^*_p H:{ 0,1}∗→Zp∗​

记输入为$x$，用SHA256哈希函数实现$H$，且${\log }_2(p)>256$。注： 这里的哈希函数$H$在密码方案中一般被当成随机谕言机。

• 参考答案：网址

直接思路：$\left(SHA256(x)\mathrm{mod}(p-1)\right)+1$。直接模$p$无法保证哈希结果不为零。模$(p-1)$使得值域为$[0,p-2]$，加1使得值域为$[1,p-1]$。

由于哈希函数$SHA256(x)<2^{256}$，而${\mathbb{Z}}_p^{\ast }$元素比特串长度大于256，所以上述思路无法做到与随机函数$f:y\leftarrow {\mathbb{Z}}_p^{\ast }$不可取分，即${\mathbb{Z}}_p^{\ast }$中有一些元素总是取不到，这与随机谕言机的定义冲突。

改进思路： 拓展SHA256的长度。

记$k=1+\lceil {\log }_2(p)/256\rceil$，利用HMAC构造$k$个不同的输出为256比特的哈希函数$H_i(x)$，HMAC的定义详见维基百科。

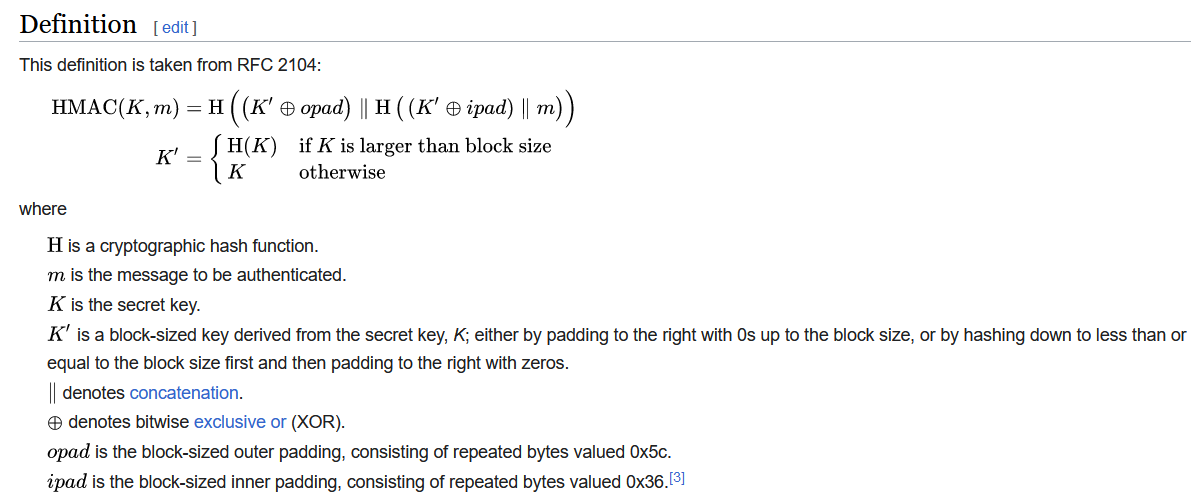
具体而言，对$H_i(x)$，随机选取512比特的种子$c_i$，使

$H_i(x)=SHA256((c_i\oplus \mathsf{opad}\Vert SHA256((c_i\oplus \mathsf{ipad}\Vert x\left)\right)$。

最终构造

$\left(\right(H_0(x)\Vert H_1(x)\Vert \cdots \Vert H_{k-1}(x))\mathrm{mod}(p-1))+1$。

扩展之后，取模之前的数的长度肯定大于${\log }_2(p)$。

我的疑问： 这里怎么保证抗碰撞性质？即使HMAC是抗碰撞的，那么攻击者不可以利用$(p-1)$的循环制造扩展哈希的碰撞对吗？例如：攻击者分别给出5的原像和$(p-1+5)$的原像。为了解决这个问题，可不可以一旦检测到$H_0\Vert \cdots \Vert H_{k-1}\ge (p-1)$，就对$x$加一个随机成分$\gamma$，利用雪崩效应使$H_0\Vert \cdots \Vert H_{k-1}<(p-1)$？

如何实现 H : Z p ∗ → { 0 , 1 } λ H: \mathbb{Z}^*_p \to \{0, 1\}^\lambda H:Zp∗​→{ 0,1}λ

跟上述做法类似，用$2^{\lambda }$取模。

参考答案：网址

如何实现 $H:\mathcal{M}\to {\mathbb{Z}}_N^{\ast }$

这里$\mathcal{M}$是消息（message）的定义域，$N$是大素数$p$和$q$的积。

参考答案：网址

主要思路：${\mathbb{Z}}_N^{\ast }$不包含$p,q,0$，那么可以直接用哈希函数对$N$取模。只要$N$足够大，刚好取到$p,q,0$的概率为可忽略函数。

个人思考： 若运气不好刚好取到$p,q,0$，则对$m\in \mathcal{M}$填充随机成分。

如何实现 H : { 0 , 1 } ∗ → G H: \{0, 1\}^* \to \mathbb{G} H:{ 0,1}∗→G

可以先将输入$x$映射至${\mathbb{Z}}_q$得到$h$，再将$g^h$作为哈希输出。这里的$g$是群的生成元。

双线性对上的哈希函数

PBC library和Charm-Crypto library都有提供相应函数，不再赘述。